Giải Bài Tập 1.38 Trang 43 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.38 trang 43 SGK Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
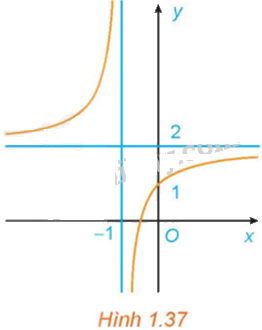
Đồ thị trong Hình 1.37 là đồ thị của hàm số:
A. \(y = \frac{{x + 2}}{{x + 1}}\).
B. \(y = \frac{{2x + 1}}{{x + 1}}\).
C. \(y = \frac{{x - 1}}{{x + 1}}\).
D. \(y = \frac{{x + 3}}{{1 - x}}\).
Giải Bài Tập 1.38 Trang 43 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 1.38 trang 43 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu chúng ta vận dụng kiến thức về đạo hàm của hàm số để giải quyết. Cụ thể, bài toán thường liên quan đến việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, hoặc tìm cực trị của hàm số.
Đề Bài Bài Tập 1.38 Trang 43 Toán 12 Tập 1 - Kết Nối Tri Thức
(Đề bài cụ thể của bài tập 1.38 sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) có đạo hàm f'(x) = (x-1)(x+2). Tìm khoảng đồng biến, nghịch biến của hàm số.)
Phương Pháp Giải Bài Tập Đạo Hàm
Để giải quyết bài tập về đạo hàm, chúng ta cần nắm vững các kiến thức sau:
- Định nghĩa đạo hàm: f'(x) = lim (h->0) [f(x+h) - f(x)] / h
- Các quy tắc tính đạo hàm: Đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của x^n, sinx, cosx, tanx, e^x, ln(x),...
- Ứng dụng của đạo hàm:
- Xác định khoảng đồng biến, nghịch biến.
- Tìm cực trị của hàm số.
- Giải các bài toán liên quan đến tối ưu hóa.
Lời Giải Chi Tiết Bài Tập 1.38 Trang 43 Toán 12 Tập 1 - Kết Nối Tri Thức
(Lời giải chi tiết của bài tập 1.38 sẽ được trình bày ở đây. Bao gồm các bước giải, giải thích rõ ràng và kết luận.)
Ví dụ, nếu đề bài là: Cho hàm số y = f(x) có đạo hàm f'(x) = (x-1)(x+2). Tìm khoảng đồng biến, nghịch biến của hàm số.
- Bước 1: Xác định dấu của f'(x)
f'(x) = (x-1)(x+2) = 0 khi x = 1 hoặc x = -2.
Xét các khoảng:
- x < -2: f'(x) > 0 (hàm số đồng biến)
- -2 < x < 1: f'(x) < 0 (hàm số nghịch biến)
- x > 1: f'(x) > 0 (hàm số đồng biến)
- Bước 2: Kết luận
Hàm số đồng biến trên các khoảng (-∞; -2) và (1; +∞).
Hàm số nghịch biến trên khoảng (-2; 1).
Các Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tham khảo thêm các bài tập tương tự sau:
- Bài tập 1.39 trang 43 SGK Toán 12 tập 1 Kết nối tri thức
- Bài tập 1.40 trang 44 SGK Toán 12 tập 1 Kết nối tri thức
Lưu Ý Khi Giải Bài Tập Đạo Hàm
Khi giải bài tập về đạo hàm, các em cần lưu ý:
- Nắm vững các quy tắc tính đạo hàm.
- Kiểm tra kỹ dấu của đạo hàm để xác định khoảng đồng biến, nghịch biến.
- Sử dụng các kiến thức về cực trị để giải quyết các bài toán tối ưu hóa.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về cách giải bài tập 1.38 trang 43 SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tập tốt!