Giải bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho quá trình học tập của các em.
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 3{x^2} - 9x + 35) trên đoạn (left[ { - 4;4} right]). b) (y = - 3{x^4} + 4{x^2} + sqrt 2 ) trên đoạn (left[ { - 1;1} right]). c) (y = x + frac{{sqrt 5 }}{x}) trên đoạn (left[ {1;10} right]). d) (y = sin 2x - x) trên đoạn (left[ { - frac{pi }{2};frac{pi }{2}} right]).
Đề bài
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\).
b) \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\).
c) \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\).
d) \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các cú pháp lệnh trong GeoGebra để thực hiện:

Lời giải chi tiết
a) Để tìm giá trị lớn nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) ta nhập Max (<\({x^3} - 3{x^2} - 9x + 35\)>,,)
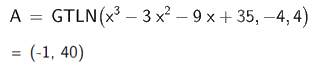
Vậy giá trị lớn nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) là 40.
Để tìm giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) ta nhập Min (<\({x^3} - 3{x^2} - 9x + 35\)>,,)
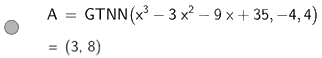
Vậy giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ { - 4;4} \right]\) là 8.
b) Để tìm giá trị lớn nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) ta nhập Max (<\( - 3{x^4} + 4{x^2} + \sqrt 2 \)>,,)
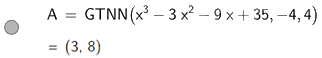
Vậy giá trị lớn nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) là 40.
Để tìm giá trị nhỏ nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) ta nhập Min (<\( - 3{x^4} + 4{x^2} + \sqrt 2 \)>,,)
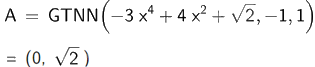
Vậy giá trị nhỏ nhất của hàm số \(y = - 3{x^4} + 4{x^2} + \sqrt 2 \) trên đoạn \(\left[ { - 1;1} \right]\) là \(\sqrt 2 \).
c) Để tìm giá trị lớn nhất của hàm số \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\) ta nhập Max (<\(x + \frac{{\sqrt 5 }}{x}\)>,,)

Vậy giá trị lớn nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) trên đoạn \(\left[ {1;10} \right]\) là \(10 + \frac{{\sqrt 5 }}{{10}}\).
Để tìm giá trị nhỏ nhất của hàm số \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\) ta nhập Min (<\(x + \frac{{\sqrt 5 }}{x}\)>,,)
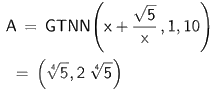
Vậy giá trị nhỏ nhất của hàm số \(y = x + \frac{{\sqrt 5 }}{x}\) trên đoạn \(\left[ {1;10} \right]\) là \(2\sqrt[4]{5}\).
d) Để tìm giá trị lớn nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) ta nhập Max (<\(\sin 2x - x\)>, <\( - \frac{\pi }{2}\)>, <\(\frac{\pi }{2}\)>)

Vậy giá trị lớn nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \(\frac{{\sqrt 3 }}{2} - \frac{\pi }{6}\).
Để tìm giá trị nhỏ nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) ta nhập Min (<\(\sin 2x - x\)>, <\( - \frac{\pi }{2}\)>, <\(\frac{\pi }{2}\)>)
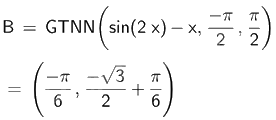
Vậy giá trị nhỏ nhất của hàm số \(y = \sin 2x - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{{\sqrt 3 }}{2} + \frac{\pi }{6}\).
Giải bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Nội dung chính của bài 3 trang 91
- Tính đạo hàm của các hàm số lượng giác (sin, cos, tan, cot).
- Vận dụng quy tắc đạo hàm của hàm hợp.
- Giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Lời giải chi tiết bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức
Câu a: Tính đạo hàm của hàm số y = sin(2x + 1)
Để tính đạo hàm của hàm số y = sin(2x + 1), ta sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Trong trường hợp này, u(t) = sin(t) và v(x) = 2x + 1.
Ta có: u'(t) = cos(t) và v'(x) = 2.
Vậy, y' = cos(2x + 1) * 2 = 2cos(2x + 1).
Câu b: Tính đạo hàm của hàm số y = cos(x^2)
Tương tự như câu a, ta sử dụng quy tắc đạo hàm của hàm hợp.
Trong trường hợp này, u(t) = cos(t) và v(x) = x^2.
Ta có: u'(t) = -sin(t) và v'(x) = 2x.
Vậy, y' = -sin(x^2) * 2x = -2xsin(x^2).
Câu c: Tính đạo hàm của hàm số y = tan(3x - 2)
Áp dụng quy tắc đạo hàm của hàm hợp, với u(t) = tan(t) và v(x) = 3x - 2.
Ta có: u'(t) = 1/cos^2(t) và v'(x) = 3.
Vậy, y' = (1/cos^2(3x - 2)) * 3 = 3/(cos^2(3x - 2)).
Mẹo giải nhanh và hiệu quả
Để giải nhanh các bài tập về đạo hàm, các em cần nắm vững các quy tắc đạo hàm cơ bản và quy tắc đạo hàm của hàm hợp. Ngoài ra, việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp các em làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Bài tập tương tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = sin(x^3 + 1).
- Tính đạo hàm của hàm số y = cos(2x^2 - 3).
- Tính đạo hàm của hàm số y = tan(x/2).
Kết luận
Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên, các em đã hiểu rõ cách giải bài 3 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Hàm số | Đạo hàm |
|---|---|
| y = sin(2x + 1) | y' = 2cos(2x + 1) |
| y = cos(x^2) | y' = -2xsin(x^2) |
| y = tan(3x - 2) | y' = 3/(cos^2(3x - 2)) |