Giải Bài Tập 1.4 Trang 13 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 1.4 trang 13 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Xét chiều biến thiên của các hàm số sau:
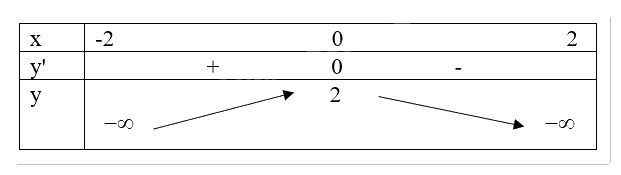
a) (y = sqrt {4 - {x^2}} );
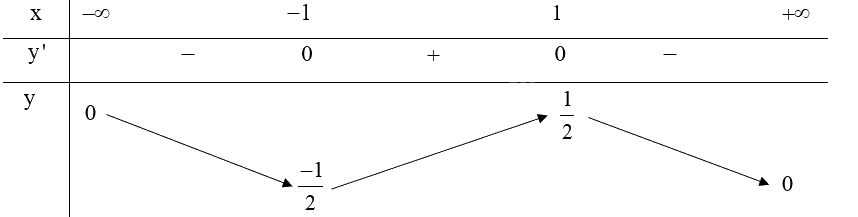
b) (y = frac{x}{{{x^2} + 1}}).
Giải Bài Tập 1.4 Trang 13 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 1.4 trang 13 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường xoay quanh việc xác định tập xác định của hàm số, tìm tập giá trị, và xét tính đơn điệu của hàm số. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Phần 1: Đề Bài Bài Tập 1.4 Trang 13
Trước khi đi vào giải, chúng ta cùng xem lại đề bài của bài tập 1.4 trang 13 SGK Toán 12 tập 1 Kết nối tri thức:
(Đề bài cụ thể của bài tập 1.4 sẽ được chèn vào đây. Ví dụ: Xác định tập xác định của hàm số f(x) = √(x-2)/(x+1))
Phần 2: Phương Pháp Giải
Để giải bài tập này, bạn cần nắm vững các kiến thức sau:
- Tập xác định của hàm số: Là tập hợp tất cả các giá trị của x sao cho hàm số f(x) có nghĩa.
- Điều kiện xác định của hàm số: Ví dụ, với hàm số chứa căn bậc chẵn, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0. Với hàm số phân thức, mẫu số khác 0.
- Tính đơn điệu của hàm số: Sử dụng đạo hàm để xét dấu và kết luận về tính đơn điệu.
Phần 3: Lời Giải Chi Tiết
Lời giải:
(Lời giải chi tiết của bài tập 1.4 sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và kết luận cuối cùng.)
Ví dụ, nếu đề bài là: Xác định tập xác định của hàm số f(x) = √(x-2)/(x+1)
- Điều kiện xác định:
- x - 2 ≥ 0 => x ≥ 2
- x + 1 ≠ 0 => x ≠ -1
- Kết hợp điều kiện: x ≥ 2 và x ≠ -1. Vì x ≥ 2 đã bao gồm x ≠ -1 nên tập xác định là [2, +∞).
Kết luận: Tập xác định của hàm số f(x) = √(x-2)/(x+1) là [2, +∞).
Phần 4: Bài Tập Tương Tự
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
- Bài tập 1.5 trang 13 SGK Toán 12 tập 1 Kết nối tri thức
- Bài tập 1.6 trang 14 SGK Toán 12 tập 1 Kết nối tri thức
Phần 5: Lời Khuyên và Lưu Ý
Khi giải các bài tập về hàm số, bạn nên:
- Đọc kỹ đề bài và xác định đúng loại hàm số.
- Nắm vững các kiến thức cơ bản về tập xác định, tập giá trị, tính đơn điệu.
- Thực hành giải nhiều bài tập để làm quen với các dạng bài khác nhau.
Hy vọng bài viết này đã giúp bạn hiểu rõ cách giải bài tập 1.4 trang 13 SGK Toán 12 tập 1 Kết nối tri thức. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại bình luận bên dưới. Chúc bạn học tốt!
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục tri thức!