Giải mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu mục 1 trang 46,47,48 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của các em.
Vectơ trong không gian
CH
Trả lời câu hỏi Câu hỏi trang 47 SGK Toán 12 Kết nối tri thức
Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải bài toán: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Giả sử có ba vectơ \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) sao cho: \(\overrightarrow a = \overrightarrow b \) và \(\overrightarrow b = \overrightarrow c \).
Vì \(\overrightarrow a = \overrightarrow b \) nên hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\) (1)
Vì \(\overrightarrow b = \overrightarrow c \) nên hai vectơ \(\overrightarrow c \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow c } \right| = \left| {\overrightarrow b } \right|\) (2)
Từ (1) và (2) ta có hai vectơ \(\overrightarrow a \), \(\overrightarrow c \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow c } \right|\). Do đó, \(\overrightarrow a = \overrightarrow c \)
Do đó, hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó bằng nhau.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 46 SGK Toán 12 Kết nối tri thức
Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.

a) Các đoạn thẳng này cho biết gì về hướng và độ lớn của các các lực căng dây?
b) Các đoạn thẳng này có cùng nằm trong một mặt phẳng không?
Phương pháp giải:
Sử dụng kiến thức về biểu diễn lực qua đoạn thẳng có hướng: Dùng đoạn thẳng có hướng để biểu diễn lực căng dây. Hướng của đoạn thẳng chỉ hướng của của lực căng dây, độ dài đoạn thẳng thể hiện độ lớn của lực và được lấy tỉ lệ với độ lớn của lực.
Lời giải chi tiết:
a) Các đoạn thẳng này có hướng lên trên (về phía móc cần cẩu) và độ dài của các đoạn thẳng thể hiện cho độ lớn của các lực căng dây và được lấy tỉ lệ với độ lớn của các lực căng dây.
b) Các đoạn thẳng này không cùng nằm trên một mặt phẳng.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 47 SGK Toán 12 Kết nối tri thức
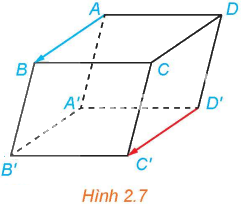
Cho hình hộp ABCD.A’B’C’D’ (H.2.7)
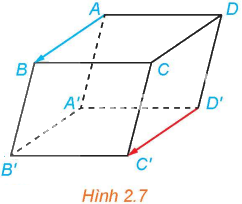
a) So sánh độ dài hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
b) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) có cùng phương không? Có cùng hướng không?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ: Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về độ dài vectơ: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
a) Vì ABCD.A’B’C’D’ là hình hộp nên ABCD và DCC’D’ là các hình bình hành. Suy ra, \(AB = CD = D'C'\). Do đó, \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {D'C'} } \right|\).
b) Vì ABCD và DCC’D’ là các hình bình hành nên AB//CD, CD//C’D’. Do đó, AB//C’D’. Vậy giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) song song với nhau.
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) cùng phương và cùng hướng.
LT1
Trả lời câu hỏi Luyện tập trang 47 SGK Toán 12 Kết nối tri thức
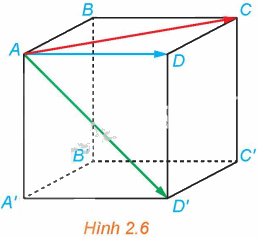
Cho hình lập phương ABCD.A’B’C’D’ (H.2.6). Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \):
a) Hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD)?
b) Hai vectơ nào có cùng độ dài?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ để tìm vectơ có giá nằm trong mặt phẳng (ABCD): Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về độ dài vectơ để tìm hai vectơ có cùng độ dài: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\)
Lời giải chi tiết:
a) Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \), hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} \) có giá nằm trong mặt phẳng (ABCD)
b) Vì ABCD.A’B’C’D’ là hình lập phương nên \(AD = DC = DD'\)
Tam giác ADD’ vuông tại D nên theo định lý Pythagore ta có:
\(AD' = \sqrt {A{D^2} + DD{'^2}} = AD\sqrt 2 \)
Tam giác ADC vuông tại D nên theo định lý Pythagore ta có:
\(AC = \sqrt {A{D^2} + D{C^2}} = AD\sqrt 2 \)
Do đó, \(AD' = AC\) hay \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD'} } \right|\). Vậy hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD'} \) có cùng độ dài.
LT2
Trả lời câu hỏi Luyện tập 2 trang 48 SGK Toán 12 Kết nối tri thức
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành.
a) Trong ba vectơ \(\overrightarrow {SC} ,\overrightarrow {AD} \) và \(\overrightarrow {DC} \), vectơ nào bằng vectơ \(\overrightarrow {AB} \).
b) Gọi M là một điểm thuộc cạnh AD. Xác định điểm N sao cho \(\overrightarrow {MN} = \overrightarrow {AB} \).
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải bài toán: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
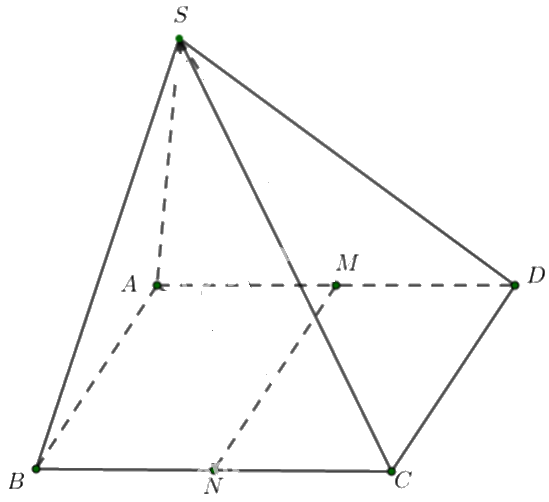
a) Vì ABCD là hình bình hành nên AB//CD và \(AB = CD\). Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) có cùng độ dài và cùng hướng nên hai vectơ đó bằng nhau.
Vì AB và SC chéo nhau nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không cùng phương. Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không bằng nhau.
Vì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không cùng phương nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không bằng nhau.
b) Qua M vẽ đường thẳng song song với AB cắt BC tại N.
Tứ giác ABNM có: AB//MN, AM//BN nên tứ giác ABNM là hình bình hành. Do đó, \(AB = MN\), lại có: AB//MN nên hai vectơ \(\overrightarrow {MN} ,\overrightarrow {AB} \) cùng độ dài và cùng hướng. Suy ra, \(\overrightarrow {MN} = \overrightarrow {AB} \). Vậy điểm N cần tìm là giao điểm của đường thẳng qua M song song với AB và cạnh BC.
VD1
Trả lời câu hỏi Vận dụng 1 trang 48 SGK Toán 12 Kết nối tri thức
Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.

Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải thích: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 15 lên tầng 22 của tòa nhà là \(\overrightarrow a \). Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 22 lên tầng 29 của tòa nhà là \(\overrightarrow b \).
Vì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều dịch chuyển từ tầng thấp lên tầng cao nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có cùng hướng (1).
Độ dài vectơ \(\overrightarrow a \) là: \(\left| {\overrightarrow a } \right| = 7\), độ dài vectơ \(\overrightarrow b \) là: \(\left| {\overrightarrow b } \right| = 7\) nên \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 7\) (2)
Từ (1) và (2) ta có: \(\overrightarrow a = \overrightarrow b \). Vậy các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau.
CH
Trả lời câu hỏi Câu hỏi trang 6 SGK Toán 12 Kết nối tri thức
Hình 2.3 cho ta ví dụ về một số đại lượng có thể biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.

Phương pháp giải:
Sử dụng kiến thức về nhận biết vectơ trong không gian để tìm hình ảnh thực tế: Vectơ trong không gian là một đoạn thẳng có hướng.
Lời giải chi tiết:
Một số ví dụ khác:
a) Hướng bay của khinh khí cầu:

b) Hướng đi của thuyền trên sông:

- HĐ1
- CH
- LT1
- HĐ2
- CH
- LT2
- VD1
Trả lời câu hỏi Hoạt động 1 trang 46 SGK Toán 12 Kết nối tri thức
Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.

a) Các đoạn thẳng này cho biết gì về hướng và độ lớn của các các lực căng dây?
b) Các đoạn thẳng này có cùng nằm trong một mặt phẳng không?
Phương pháp giải:
Sử dụng kiến thức về biểu diễn lực qua đoạn thẳng có hướng: Dùng đoạn thẳng có hướng để biểu diễn lực căng dây. Hướng của đoạn thẳng chỉ hướng của của lực căng dây, độ dài đoạn thẳng thể hiện độ lớn của lực và được lấy tỉ lệ với độ lớn của lực.
Lời giải chi tiết:
a) Các đoạn thẳng này có hướng lên trên (về phía móc cần cẩu) và độ dài của các đoạn thẳng thể hiện cho độ lớn của các lực căng dây và được lấy tỉ lệ với độ lớn của các lực căng dây.
b) Các đoạn thẳng này không cùng nằm trên một mặt phẳng.
Trả lời câu hỏi Câu hỏi trang 6 SGK Toán 12 Kết nối tri thức
Hình 2.3 cho ta ví dụ về một số đại lượng có thể biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.

Phương pháp giải:
Sử dụng kiến thức về nhận biết vectơ trong không gian để tìm hình ảnh thực tế: Vectơ trong không gian là một đoạn thẳng có hướng.
Lời giải chi tiết:
Một số ví dụ khác:
a) Hướng bay của khinh khí cầu:

b) Hướng đi của thuyền trên sông:

Trả lời câu hỏi Luyện tập trang 47 SGK Toán 12 Kết nối tri thức
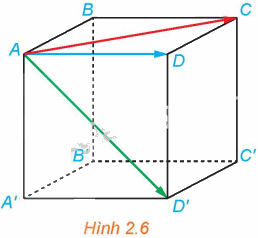
Cho hình lập phương ABCD.A’B’C’D’ (H.2.6). Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \):
a) Hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD)?
b) Hai vectơ nào có cùng độ dài?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ để tìm vectơ có giá nằm trong mặt phẳng (ABCD): Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về độ dài vectơ để tìm hai vectơ có cùng độ dài: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\)
Lời giải chi tiết:
a) Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \), hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} \) có giá nằm trong mặt phẳng (ABCD)
b) Vì ABCD.A’B’C’D’ là hình lập phương nên \(AD = DC = DD'\)
Tam giác ADD’ vuông tại D nên theo định lý Pythagore ta có:
\(AD' = \sqrt {A{D^2} + DD{'^2}} = AD\sqrt 2 \)
Tam giác ADC vuông tại D nên theo định lý Pythagore ta có:
\(AC = \sqrt {A{D^2} + D{C^2}} = AD\sqrt 2 \)
Do đó, \(AD' = AC\) hay \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AD'} } \right|\). Vậy hai vectơ \(\overrightarrow {AC} ,\overrightarrow {AD'} \) có cùng độ dài.
Trả lời câu hỏi Hoạt động 2 trang 47 SGK Toán 12 Kết nối tri thức
Cho hình hộp ABCD.A’B’C’D’ (H.2.7)
a) So sánh độ dài hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
b) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) có cùng phương không? Có cùng hướng không?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ: Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về độ dài vectơ: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
a) Vì ABCD.A’B’C’D’ là hình hộp nên ABCD và DCC’D’ là các hình bình hành. Suy ra, \(AB = CD = D'C'\). Do đó, \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {D'C'} } \right|\).
b) Vì ABCD và DCC’D’ là các hình bình hành nên AB//CD, CD//C’D’. Do đó, AB//C’D’. Vậy giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) song song với nhau.
c) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \) cùng phương và cùng hướng.
Trả lời câu hỏi Câu hỏi trang 47 SGK Toán 12 Kết nối tri thức
Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải bài toán: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Giả sử có ba vectơ \(\overrightarrow a \), \(\overrightarrow b \) và \(\overrightarrow c \) sao cho: \(\overrightarrow a = \overrightarrow b \) và \(\overrightarrow b = \overrightarrow c \).
Vì \(\overrightarrow a = \overrightarrow b \) nên hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\) (1)
Vì \(\overrightarrow b = \overrightarrow c \) nên hai vectơ \(\overrightarrow c \), \(\overrightarrow b \) có cùng hướng và \(\left| {\overrightarrow c } \right| = \left| {\overrightarrow b } \right|\) (2)
Từ (1) và (2) ta có hai vectơ \(\overrightarrow a \), \(\overrightarrow c \) có cùng hướng và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow c } \right|\). Do đó, \(\overrightarrow a = \overrightarrow c \)
Do đó, hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó bằng nhau.
Trả lời câu hỏi Luyện tập 2 trang 48 SGK Toán 12 Kết nối tri thức
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành.
a) Trong ba vectơ \(\overrightarrow {SC} ,\overrightarrow {AD} \) và \(\overrightarrow {DC} \), vectơ nào bằng vectơ \(\overrightarrow {AB} \).
b) Gọi M là một điểm thuộc cạnh AD. Xác định điểm N sao cho \(\overrightarrow {MN} = \overrightarrow {AB} \).
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải bài toán: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
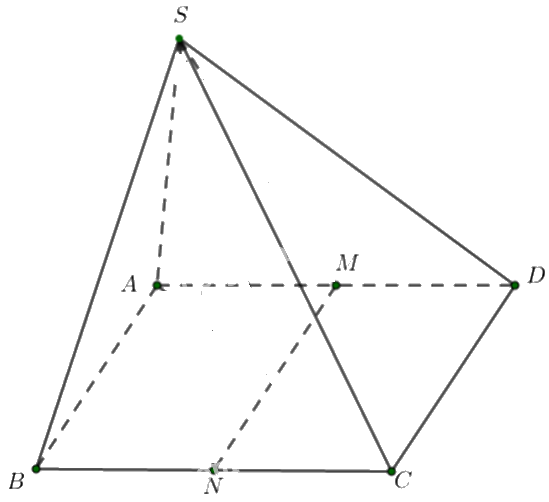
a) Vì ABCD là hình bình hành nên AB//CD và \(AB = CD\). Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) có cùng độ dài và cùng hướng nên hai vectơ đó bằng nhau.
Vì AB và SC chéo nhau nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không cùng phương. Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \) không bằng nhau.
Vì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không cùng phương nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) không bằng nhau.
b) Qua M vẽ đường thẳng song song với AB cắt BC tại N.
Tứ giác ABNM có: AB//MN, AM//BN nên tứ giác ABNM là hình bình hành. Do đó, \(AB = MN\), lại có: AB//MN nên hai vectơ \(\overrightarrow {MN} ,\overrightarrow {AB} \) cùng độ dài và cùng hướng. Suy ra, \(\overrightarrow {MN} = \overrightarrow {AB} \). Vậy điểm N cần tìm là giao điểm của đường thẳng qua M song song với AB và cạnh BC.
Trả lời câu hỏi Vận dụng 1 trang 48 SGK Toán 12 Kết nối tri thức
Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.

Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải thích: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 15 lên tầng 22 của tòa nhà là \(\overrightarrow a \). Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 22 lên tầng 29 của tòa nhà là \(\overrightarrow b \).
Vì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều dịch chuyển từ tầng thấp lên tầng cao nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có cùng hướng (1).
Độ dài vectơ \(\overrightarrow a \) là: \(\left| {\overrightarrow a } \right| = 7\), độ dài vectơ \(\overrightarrow b \) là: \(\left| {\overrightarrow b } \right| = 7\) nên \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 7\) (2)
Từ (1) và (2) ta có: \(\overrightarrow a = \overrightarrow b \). Vậy các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau.
Giải mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Đây là một phần kiến thức nền tảng quan trọng, thường xuyên xuất hiện trong các bài kiểm tra và kỳ thi THPT Quốc gia. Việc nắm vững kiến thức này không chỉ giúp các em giải quyết các bài toán cụ thể mà còn phát triển tư duy logic và khả năng phân tích.
Nội dung chính của Mục 1
- Ôn tập khái niệm đạo hàm: Định nghĩa đạo hàm, quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Ứng dụng đạo hàm để khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn của hàm số.
- Bài tập vận dụng: Giải các bài tập liên quan đến việc tính đạo hàm, khảo sát hàm số và ứng dụng đạo hàm để giải quyết các bài toán thực tế.
Hướng dẫn giải chi tiết các bài tập trong Mục 1
Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức:
Bài 1: Tính đạo hàm của các hàm số sau
Để tính đạo hàm của một hàm số, các em cần áp dụng các quy tắc tính đạo hàm đã học. Ví dụ, để tính đạo hàm của hàm số y = x2 + 2x - 1, ta sử dụng quy tắc đạo hàm của hàm đa thức:
y' = 2x + 2
Bài 2: Khảo sát hàm số y = x3 - 3x + 2
Để khảo sát hàm số, các em cần thực hiện các bước sau:
- Xác định tập xác định của hàm số.
- Tính đạo hàm bậc nhất y'.
- Giải phương trình y' = 0 để tìm các điểm cực trị.
- Lập bảng biến thiên của hàm số.
- Kết luận về khoảng đồng biến, nghịch biến, cực trị và điểm uốn của hàm số.
Bài 3: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = -x2 + 4x - 3 trên đoạn [-1; 3]
Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn, các em cần thực hiện các bước sau:
- Tính đạo hàm y'.
- Giải phương trình y' = 0 để tìm các điểm cực trị nằm trong đoạn.
- Tính giá trị của hàm số tại các điểm cực trị và tại các mút của đoạn.
- So sánh các giá trị để tìm ra giá trị lớn nhất và giá trị nhỏ nhất.
Lưu ý khi giải các bài tập về đạo hàm và ứng dụng
- Nắm vững các quy tắc tính đạo hàm.
- Hiểu rõ các bước khảo sát hàm số.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
Tusach.vn hy vọng rằng với hướng dẫn chi tiết này, các em sẽ hiểu rõ hơn về Mục 1 trang 46,47,48 SGK Toán 12 tập 1 - Kết nối tri thức và tự tin giải các bài tập liên quan. Chúc các em học tập tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | Xem chi tiết tại đây |
| Bài 2 | Xem chi tiết tại đây |
| Bài 3 | Xem chi tiết tại đây |