Giải mục 1 trang 29,30,31 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 29,30,31 SGK Toán 12 tập 2 - Kết nối tri thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 2 - Kết nối tri thức. Mục 1 trang 29, 30, 31 tập trung vào các kiến thức quan trọng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi hiểu rằng việc tự học và làm bài tập có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của tusach.vn đã biên soạn lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng
LT1
Trả lời câu hỏi Luyện tập 1 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2;3} \right),B\left( { - 3;0;1} \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB. Hãy chỉ ra một vectơ pháp tuyến của \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Vì \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB nên giá của \(\overrightarrow {AB} \bot \left( \alpha \right)\).
Do đó, một vectơ pháp tuyến của \(\left( \alpha \right)\) là \(\overrightarrow {AB} \left( { - 4;2; - 2} \right)\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a,b,c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\).
a) Vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) có vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay không?
b) \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về tích vô hướng của 2 vectơ để chứng minh: Trong không gian Oxyz, tích vô hướng của 2 vectơ \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = xx' + yy' + zz'\).
Lời giải chi tiết:
a) Ta có: \(\overrightarrow n .\overrightarrow u = a\left( {bc' - b'c} \right) + b\left( {ca' - c'a} \right) + c\left( {ab' - a'b} \right)\)
\( = abc' - ab'c + cba' - abc' + ab'c - a'bc = \left( {abc' - abc'} \right) - \left( {ab'c - ab'c} \right) + \left( {cba' - cba'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow u \).
Ta có: \(\overrightarrow n .\overrightarrow v = a'\left( {bc' - b'c} \right) + b'\left( {ca' - c'a} \right) + c'\left( {ab' - a'b} \right)\)
\( = a'bc' - a'b'c + cb'a' - ab'c' + ab'c' - a'bc'\)
\( = \left( {a'bc' - a'bc'} \right) - \left( {a'b'c - a'b'c} \right) + \left( {ab'c' - ab'c'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow v \).
Suy ra, vectơ \(\overrightarrow n \) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Nếu \(\overrightarrow n = \overrightarrow 0 \) thì \(\left\{ \begin{array}{l}bc' - b'c = 0\\ca' - c'a = 0\\ab' - a'b = 0\end{array} \right.\left( I \right)\)
+ Với \(a = 0,b = 0,c = 0\) thì (I) luôn đúng. Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
+ Với \(a \ne 0,b \ne 0,c \ne 0\), từ (I) ta có: \(\left\{ \begin{array}{l}\frac{{b'}}{b} = \frac{{c'}}{c}\\\frac{{a'}}{a} = \frac{{c'}}{c}\\\frac{{b'}}{b} = \frac{{a'}}{a}\end{array} \right.\), do đó, \(a' = ka,b' = kb,c' = kc\;\;\left( {k \in \mathbb{R}} \right)\)
Suy ra: \(\overrightarrow v = k\overrightarrow u \). Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
Vậy \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
LT2
Trả lời câu hỏi Luyện tập 2 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {2;3;1} \right)\) và \(\overrightarrow v = \left( {4;6;2} \right)\). Tính \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
Ta có: \(\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {\left| \begin{array}{l}3\;\;1\\6\;\;2\end{array} \right|;\left| \begin{array}{l}1\;\;2\\2\;\;4\end{array} \right|;\left| \begin{array}{l}2\;\;3\\4\;\;6\end{array} \right|} \right) = \left( {0;0;0} \right)\)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của nó có vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) hay không?
b) Mặt phẳng (P) có nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến hay không?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để chứng minh: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để chứng minh: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\)vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nếu hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương.
b) Vì hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P), mà vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có giá vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nên giá của vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) vuông góc với mặt phẳng (P). Suy ra, mặt phẳng (P) nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến.
LT3
Trả lời câu hỏi Luyện tập 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1; - 2;1} \right),B\left( { - 2;1;0} \right),C\left( { - 2;3;2} \right)\). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (ABC).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Trong không gian Oxyz, nếu \(\overrightarrow u \), \(\overrightarrow v \) là cặp vectơ chỉ phương của (P) thì \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) là một vectơ pháp tuyến của (P).
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} \left( { - 3;3; - 1} \right),\overrightarrow {AC} = \left( { - 3;5;1} \right)\). Vì \(\overrightarrow {AB} ,\overrightarrow {AC} \) là các vectơ chỉ phương của mặt phẳng (ABC) nên mặt phẳng (ABC) nhận \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\) làm một vectơ pháp tuyến.
\(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| \begin{array}{l}3\;\;\; - 1\\\;5\;\;\;\;\;1\end{array} \right|;\left| \begin{array}{l} - 1\;\; - 3\\\;\;1\;\; - 3\end{array} \right|;\left| \begin{array}{l} - 3\;\;3\\ - 3\;\;5\end{array} \right|} \right) = \left( {8;6; - 6} \right)\)
HĐ1
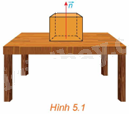
Trả lời câu hỏi Hoạt động 1 trang 29 SGK Toán 12 Kết nối tri thức
Trên mặt bàn phẳng, đặt một vật. Khi đó, mặt bàn tác động lên vật phản lực pháp tuyến \(\overrightarrow n \), giá của vectơ \(\overrightarrow n \) vuông góc với mặt bàn. Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương gì? (H.5.1)
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ để tìm phương của \(\overrightarrow n \): Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương thẳng đứng, vuông góc với mặt bàn.
VD1
Trả lời câu hỏi Vận dụng 1 trang 31 SGK Toán 12 Kết nối tri thức
Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể. Trong không gian Oxyz, với đơn vị đo là mét, nếu tác động vào cán mỏ lết tại vị trí P một lực \(\overrightarrow F \) để vặn con ốc ở vị trí O (H.5.6) thì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\).
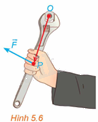
a) Cho \(\overrightarrow {OP} = \left( {x;y;z} \right),\overrightarrow F = \left( {a;b;c} \right)\), Tính \(\overrightarrow M \).
b) Giải thích vì sao, nếu giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi. Từ đó, ta có thể rút ra điều gì để đỡ tốn sức khi dùng mỏ lết vặn ốc?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
a) Ta có: \(\left[ {\overrightarrow {OP} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}y&z\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}z&x\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}x&y\\a&b\end{array}} \right|} \right) = \left( {cy - bz;za - cx;xb - ay} \right)\)
Do đó, \(\overrightarrow M = \left( {cy - bz;za - cx;xb - ay} \right)\).
b) Ta có: \(\overrightarrow {OP'} = \left( {2x;2y;2z} \right)\). Khi đó, moment lực là: \(\overrightarrow {M'} = \left[ {\overrightarrow {OP'} ,\overrightarrow F } \right]\)
Do đó, \(\left[ {\overrightarrow {OP'} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}{2y}&{2z}\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2z}&{2x}\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2x}&{2y}\\a&b\end{array}} \right|} \right) = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right)\)
Suy ra: \(\overrightarrow {M'} = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right) = 2\overrightarrow M \)
Vậy khi giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi.
Từ đó, ta rút ra kết luận là nếu tác động vào cán mỏ lết tại vị trí P cách con ốc ở vị trí O càng lớn thì càng đỡ tốn sức khi dùng mỏ lết vặn ốc.
- HĐ1
- LT1
- HĐ2
- LT2
- HĐ3
- LT3
- VD1
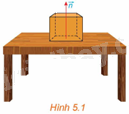
Trả lời câu hỏi Hoạt động 1 trang 29 SGK Toán 12 Kết nối tri thức
Trên mặt bàn phẳng, đặt một vật. Khi đó, mặt bàn tác động lên vật phản lực pháp tuyến \(\overrightarrow n \), giá của vectơ \(\overrightarrow n \) vuông góc với mặt bàn. Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương gì? (H.5.1)
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ để tìm phương của \(\overrightarrow n \): Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương thẳng đứng, vuông góc với mặt bàn.
Trả lời câu hỏi Luyện tập 1 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2;3} \right),B\left( { - 3;0;1} \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB. Hãy chỉ ra một vectơ pháp tuyến của \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Vì \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB nên giá của \(\overrightarrow {AB} \bot \left( \alpha \right)\).
Do đó, một vectơ pháp tuyến của \(\left( \alpha \right)\) là \(\overrightarrow {AB} \left( { - 4;2; - 2} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a,b,c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\).
a) Vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) có vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay không?
b) \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về tích vô hướng của 2 vectơ để chứng minh: Trong không gian Oxyz, tích vô hướng của 2 vectơ \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = xx' + yy' + zz'\).
Lời giải chi tiết:
a) Ta có: \(\overrightarrow n .\overrightarrow u = a\left( {bc' - b'c} \right) + b\left( {ca' - c'a} \right) + c\left( {ab' - a'b} \right)\)
\( = abc' - ab'c + cba' - abc' + ab'c - a'bc = \left( {abc' - abc'} \right) - \left( {ab'c - ab'c} \right) + \left( {cba' - cba'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow u \).
Ta có: \(\overrightarrow n .\overrightarrow v = a'\left( {bc' - b'c} \right) + b'\left( {ca' - c'a} \right) + c'\left( {ab' - a'b} \right)\)
\( = a'bc' - a'b'c + cb'a' - ab'c' + ab'c' - a'bc'\)
\( = \left( {a'bc' - a'bc'} \right) - \left( {a'b'c - a'b'c} \right) + \left( {ab'c' - ab'c'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow v \).
Suy ra, vectơ \(\overrightarrow n \) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Nếu \(\overrightarrow n = \overrightarrow 0 \) thì \(\left\{ \begin{array}{l}bc' - b'c = 0\\ca' - c'a = 0\\ab' - a'b = 0\end{array} \right.\left( I \right)\)
+ Với \(a = 0,b = 0,c = 0\) thì (I) luôn đúng. Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
+ Với \(a \ne 0,b \ne 0,c \ne 0\), từ (I) ta có: \(\left\{ \begin{array}{l}\frac{{b'}}{b} = \frac{{c'}}{c}\\\frac{{a'}}{a} = \frac{{c'}}{c}\\\frac{{b'}}{b} = \frac{{a'}}{a}\end{array} \right.\), do đó, \(a' = ka,b' = kb,c' = kc\;\;\left( {k \in \mathbb{R}} \right)\)
Suy ra: \(\overrightarrow v = k\overrightarrow u \). Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
Vậy \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
Trả lời câu hỏi Luyện tập 2 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {2;3;1} \right)\) và \(\overrightarrow v = \left( {4;6;2} \right)\). Tính \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
Ta có: \(\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {\left| \begin{array}{l}3\;\;1\\6\;\;2\end{array} \right|;\left| \begin{array}{l}1\;\;2\\2\;\;4\end{array} \right|;\left| \begin{array}{l}2\;\;3\\4\;\;6\end{array} \right|} \right) = \left( {0;0;0} \right)\)
Trả lời câu hỏi Hoạt động 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của nó có vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) hay không?
b) Mặt phẳng (P) có nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến hay không?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để chứng minh: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để chứng minh: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\)vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nếu hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương.
b) Vì hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P), mà vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có giá vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nên giá của vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) vuông góc với mặt phẳng (P). Suy ra, mặt phẳng (P) nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến.
Trả lời câu hỏi Luyện tập 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1; - 2;1} \right),B\left( { - 2;1;0} \right),C\left( { - 2;3;2} \right)\). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (ABC).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Trong không gian Oxyz, nếu \(\overrightarrow u \), \(\overrightarrow v \) là cặp vectơ chỉ phương của (P) thì \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) là một vectơ pháp tuyến của (P).
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} \left( { - 3;3; - 1} \right),\overrightarrow {AC} = \left( { - 3;5;1} \right)\). Vì \(\overrightarrow {AB} ,\overrightarrow {AC} \) là các vectơ chỉ phương của mặt phẳng (ABC) nên mặt phẳng (ABC) nhận \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\) làm một vectơ pháp tuyến.
\(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| \begin{array}{l}3\;\;\; - 1\\\;5\;\;\;\;\;1\end{array} \right|;\left| \begin{array}{l} - 1\;\; - 3\\\;\;1\;\; - 3\end{array} \right|;\left| \begin{array}{l} - 3\;\;3\\ - 3\;\;5\end{array} \right|} \right) = \left( {8;6; - 6} \right)\)
Trả lời câu hỏi Vận dụng 1 trang 31 SGK Toán 12 Kết nối tri thức
Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể. Trong không gian Oxyz, với đơn vị đo là mét, nếu tác động vào cán mỏ lết tại vị trí P một lực \(\overrightarrow F \) để vặn con ốc ở vị trí O (H.5.6) thì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\).
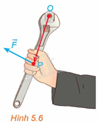
a) Cho \(\overrightarrow {OP} = \left( {x;y;z} \right),\overrightarrow F = \left( {a;b;c} \right)\), Tính \(\overrightarrow M \).
b) Giải thích vì sao, nếu giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi. Từ đó, ta có thể rút ra điều gì để đỡ tốn sức khi dùng mỏ lết vặn ốc?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
a) Ta có: \(\left[ {\overrightarrow {OP} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}y&z\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}z&x\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}x&y\\a&b\end{array}} \right|} \right) = \left( {cy - bz;za - cx;xb - ay} \right)\)
Do đó, \(\overrightarrow M = \left( {cy - bz;za - cx;xb - ay} \right)\).
b) Ta có: \(\overrightarrow {OP'} = \left( {2x;2y;2z} \right)\). Khi đó, moment lực là: \(\overrightarrow {M'} = \left[ {\overrightarrow {OP'} ,\overrightarrow F } \right]\)
Do đó, \(\left[ {\overrightarrow {OP'} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}{2y}&{2z}\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2z}&{2x}\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2x}&{2y}\\a&b\end{array}} \right|} \right) = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right)\)
Suy ra: \(\overrightarrow {M'} = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right) = 2\overrightarrow M \)
Vậy khi giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi.
Từ đó, ta rút ra kết luận là nếu tác động vào cán mỏ lết tại vị trí P cách con ốc ở vị trí O càng lớn thì càng đỡ tốn sức khi dùng mỏ lết vặn ốc.
Giải mục 1 trang 29,30,31 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và hướng dẫn chi tiết
Mục 1 của SGK Toán 12 tập 2 - Kết nối tri thức là một phần quan trọng trong chương trình học, tập trung vào việc củng cố và mở rộng kiến thức về đạo hàm. Việc nắm vững các khái niệm và kỹ năng trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 29, 30, 31, đồng thời đưa ra những lưu ý quan trọng để bạn có thể tự tin làm bài.
Nội dung chính của Mục 1
- Khái niệm đạo hàm: Ôn lại định nghĩa đạo hàm của hàm số tại một điểm và trên một khoảng.
- Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Đạo hàm của các hàm số thường gặp: Biết cách tính đạo hàm của các hàm số lượng giác, hàm mũ, hàm logarit.
- Ứng dụng của đạo hàm: Sử dụng đạo hàm để khảo sát hàm số, tìm cực trị, điểm uốn và vẽ đồ thị hàm số.
Giải chi tiết bài tập trang 29, 30, 31
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1, trang 29, 30, 31 của SGK Toán 12 tập 2 - Kết nối tri thức:
Bài 1: Tính đạo hàm của các hàm số sau:
- f(x) = x3 - 2x2 + 5x - 1
- g(x) = sin(x) + cos(x)
- h(x) = ex + ln(x)
Lời giải:
- f'(x) = 3x2 - 4x + 5
- g'(x) = cos(x) - sin(x)
- h'(x) = ex + 1/x
Bài 2: Tìm đạo hàm của hàm số y = (x2 + 1) / (x - 1)
Lời giải:
Sử dụng quy tắc đạo hàm của thương:
y' = [(2x)(x-1) - (x2 + 1)(1)] / (x-1)2 = (x2 - 2x - 1) / (x-1)2
Bài 3: Cho hàm số f(x) = x4 - 4x2 + 1. Tìm các điểm cực trị của hàm số.
Lời giải:
f'(x) = 4x3 - 8x = 4x(x2 - 2)
f'(x) = 0 khi x = 0, x = √2, x = -√2
Khảo sát dấu của f'(x) để xác định các điểm cực trị.
Kết luận: Hàm số có cực đại tại x = -√2 và x = √2, cực tiểu tại x = 0.
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các định nghĩa và quy tắc tính đạo hàm.
- Thực hành nhiều bài tập để làm quen với các dạng bài khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
- Đọc kỹ đề bài và xác định đúng các hàm số cần tính đạo hàm.
Tusach.vn – Hỗ trợ học tập Toán 12 hiệu quả
Tusach.vn cam kết cung cấp những lời giải chính xác, dễ hiểu và đầy đủ cho tất cả các bài tập trong SGK Toán 12 tập 2 - Kết nối tri thức. Chúng tôi luôn cập nhật nội dung mới nhất và lắng nghe phản hồi từ người dùng để cải thiện chất lượng dịch vụ. Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Chúc bạn học tập tốt!