Giải mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 26, 27 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập liên quan.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Sơ đồ khảo sát hàm số
Đề bài
Trả lời câu hỏi Hoạt động 1 trang 26 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = {x^2} - 4x + 3\). Thực hiện lần lượt các yêu cầu sau:
a) Tính y’ và tìm các điểm tại đó \(y' = 0\).
b) Xét dấu y’ để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
c) Tính \(\mathop {\lim }\limits_{x \to - \infty } y\), \(\mathop {\lim }\limits_{x \to + \infty } y\) và lập bảng biến thiên của hàm số.
d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.
Phương pháp giải - Xem chi tiết
a) Tính y’. Giải phương trình \(y' = 0\).
b) Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Sử dụng kiến thức về định lí cực trị hàm số để tìm cực trị hàm số: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).
d) Đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) nhận đường thẳng \(x = \frac{{ - b}}{{2a}}\) làm trục đối xứng.
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\)
Ta có: \(y' = 2x - 4,y' = 0 \Leftrightarrow 2x - 4 = 0 \Leftrightarrow x = 2\)
Vậy với \(x = 2\) thì \(y' = 0\).
b) Trên khoảng \(\left( { - \infty ;2} \right)\), \(y' < 0\) nên hàm số nghịch biến. Trên khoảng \(\left( {2; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Hàm số đạt cực tiểu tại \(x = 2,\) giá trị cực tiểu \({y_{CT}} = - 1\). Hàm số không có cực đại.
c) \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
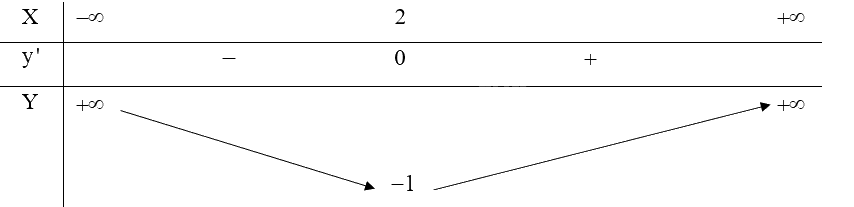
d) Đồ thị:
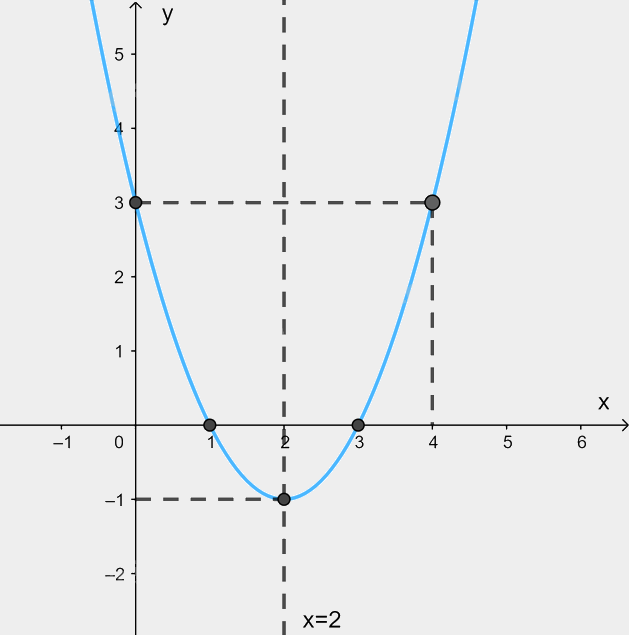
Giao điểm của đồ thị hàm số \(y = {x^2} - 4x + 3\) với trục tung là \(\left( {0;3} \right)\).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\). Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( {3;0} \right);\left( {1;0} \right)\).
Điểm \(\left( {4;3} \right)\) thuộc đồ thị hàm số \(y = {x^2} - 4x + 3\).
Đồ thị hàm số nhận đường thẳng \(x = 2\) làm trục đối xứng.
d) Đồ thị:
Giao điểm của đồ thị hàm số \(y = {x^2} - 4x + 3\) với trục tung là \(\left( {0;3} \right)\).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\). Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( {3;0} \right);\left( {1;0} \right)\).
Điểm \(\left( {4;3} \right)\) thuộc đồ thị hàm số \(y = {x^2} - 4x + 3\).
Đồ thị hàm số nhận đường thẳng \(x = 2\) làm trục đối xứng.
Giải mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Đây là một phần kiến thức nền tảng quan trọng, xuất hiện thường xuyên trong các bài thi THPT Quốc gia. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này sẽ giúp học sinh đạt kết quả tốt hơn trong môn Toán.
Nội dung chính của Mục 1
- Ôn tập về đạo hàm: Định nghĩa, các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Ứng dụng của đạo hàm: Khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn), giải phương trình, bất phương trình.
- Bài tập áp dụng: Các bài tập vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Phương pháp giải bài tập hiệu quả
- Nắm vững lý thuyết: Hiểu rõ định nghĩa, các quy tắc tính đạo hàm và ứng dụng của đạo hàm.
- Phân tích đề bài: Xác định rõ yêu cầu của đề bài, các dữ kiện đã cho và các công thức cần sử dụng.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị hàm số.
- Kiểm tra lại kết quả: Đảm bảo kết quả tính toán chính xác và phù hợp với yêu cầu của đề bài.
Giải chi tiết các bài tập trong Mục 1
Dưới đây là lời giải chi tiết các bài tập trong Mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức:
Bài 1: Tính đạo hàm của các hàm số sau
a) y = x3 - 2x2 + 5x - 1
b) y = sin(2x) + cos(x)
c) y = ex + ln(x)
(Lời giải chi tiết cho từng câu sẽ được trình bày tại đây, bao gồm các bước tính toán và giải thích rõ ràng)
Bài 2: Khảo sát hàm số y = x3 - 3x2 + 2x
(Lời giải chi tiết bao gồm các bước xác định tập xác định, tính đạo hàm, tìm cực trị, vẽ đồ thị hàm số và kết luận)
Bài 3: Giải phương trình 2x3 - 6x2 + 2 = 0
(Lời giải chi tiết sử dụng phương pháp đạo hàm để tìm nghiệm của phương trình)
Lưu ý khi học và giải bài tập
Để học tốt và giải bài tập hiệu quả, các em cần:
- Thực hành giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
- Tham khảo các tài liệu tham khảo, sách bài tập để mở rộng kiến thức.
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
- Tự kiểm tra và đánh giá kết quả học tập của mình.
tusach.vn hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả này, các em sẽ tự tin hơn trong việc học tập môn Toán 12. Chúc các em học tốt!
| Bài tập | Độ khó | Lời giải |
|---|---|---|
| Bài 1a | Dễ | Xem chi tiết |
| Bài 1b | Trung bình | Xem chi tiết |