Giải mục 3 trang 52,53 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 3 trang 52,53 SGK Toán 12 tập 2 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết mục 3 trang 52,53 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và nắm vững kiến thức liên quan đến nội dung bài học.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, cùng với các bước giải chi tiết, giúp bạn tự tin làm bài tập và đạt kết quả tốt nhất.
CÔNG THỨC TÍNH GÓC GIỮA HAI MẶT PHẲNG
VD
Trả lời câu hỏi Vận dụng trang 53 SGK Toán 12 Kết nối tri thức
Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)
Lời giải chi tiết:
Ta có: \(A\left( {0; - 2;0} \right),C\left( {0;2;0} \right),B\left( {2\sqrt 3 ;0;0} \right),A'\left( {0; - 2;7} \right),C'\left( {0;2;5} \right),B'\left( {2\sqrt 3 ;0;6} \right)\)
\(\overrightarrow {AB} \left( {2\sqrt 3 ;2;0} \right),\overrightarrow {AC} \left( {0;4;0} \right);\overrightarrow {A'B'} \left( {2\sqrt 3 ;2; - 1} \right),\overrightarrow {A'C'} \left( {0;4; - 2} \right)\)
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\4&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}0&{2\sqrt 3 }\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;0; 8\sqrt 3 } \right)\)
\(\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 2}\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 1}&{2\sqrt 3 }\\{ - 2}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;4\sqrt 3 ;8\sqrt 3 } \right)\)
Mặt phẳng (ABC) có một vectơ pháp tuyến là: \(\frac{{ 1}}{{8\sqrt 3 }}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0;0;1} \right)\)
Mặt phẳng (A’B’C’) có một vectơ pháp tuyến là: \(\frac{1}{{4\sqrt 3 }}\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {0;1;2} \right)\)
Do đó, \(\cos \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = \frac{{\left| {0.0 + 0.1 + 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {1^2} + {2^2}} }} = \frac{{2\sqrt 5 }}{5}\)
\( \Rightarrow \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) \approx 26,{6^o}\)
Vậy mái nhà nghiêng so với mặt sàn nhà một góc khoảng \(26,{1^o}\).
LT3
Trả lời câu hỏi Luyện tập 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa hai mặt phẳng \(\left( P \right):x - \sqrt 2 y + z - 2 = 0\) và \(\left( {Oxz} \right):y = 0\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\).
Lời giải chi tiết:
Mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow n \left( {1; - \sqrt 2 ;1} \right)\), mặt phẳng (Oxz) có vectơ pháp tuyến là \(\overrightarrow n \left( {0;1;0} \right)\). Ta có: \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| {0.1 - \sqrt 2 .1 + 1.0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - \sqrt 2 } \right)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}\)
Do đó, \(\left( {\left( P \right),\left( {Oxz} \right)} \right) = {45^0}\).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Lấy các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) (H.5.36)
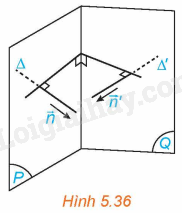
a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) có mối quan hệ gì?
b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tìm mối quan hệ: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u ,\overrightarrow {u'} \) thì \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
Lời giải chi tiết:
a) Vì các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) nên đường thẳng \(\Delta \) vuông góc với mặt phẳng (P), đường thẳng \(\Delta '\) vuông góc với mặt phẳng (Q).
Do đó, \(\left( {\left( P \right),\left( Q \right)} \right) = \left( {\Delta ,\Delta '} \right)\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\) nên \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\).
- HĐ3
- LT3
- VD
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Lấy các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) (H.5.36)
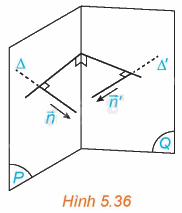
a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) có mối quan hệ gì?
b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tìm mối quan hệ: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u ,\overrightarrow {u'} \) thì \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
Lời giải chi tiết:
a) Vì các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) nên đường thẳng \(\Delta \) vuông góc với mặt phẳng (P), đường thẳng \(\Delta '\) vuông góc với mặt phẳng (Q).
Do đó, \(\left( {\left( P \right),\left( Q \right)} \right) = \left( {\Delta ,\Delta '} \right)\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\) nên \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\).
Trả lời câu hỏi Luyện tập 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa hai mặt phẳng \(\left( P \right):x - \sqrt 2 y + z - 2 = 0\) và \(\left( {Oxz} \right):y = 0\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\).
Lời giải chi tiết:
Mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow n \left( {1; - \sqrt 2 ;1} \right)\), mặt phẳng (Oxz) có vectơ pháp tuyến là \(\overrightarrow n \left( {0;1;0} \right)\). Ta có: \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| {0.1 - \sqrt 2 .1 + 1.0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - \sqrt 2 } \right)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}\)
Do đó, \(\left( {\left( P \right),\left( {Oxz} \right)} \right) = {45^0}\).
Trả lời câu hỏi Vận dụng trang 53 SGK Toán 12 Kết nối tri thức
Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)
Lời giải chi tiết:
Ta có: \(A\left( {0; - 2;0} \right),C\left( {0;2;0} \right),B\left( {2\sqrt 3 ;0;0} \right),A'\left( {0; - 2;7} \right),C'\left( {0;2;5} \right),B'\left( {2\sqrt 3 ;0;6} \right)\)
\(\overrightarrow {AB} \left( {2\sqrt 3 ;2;0} \right),\overrightarrow {AC} \left( {0;4;0} \right);\overrightarrow {A'B'} \left( {2\sqrt 3 ;2; - 1} \right),\overrightarrow {A'C'} \left( {0;4; - 2} \right)\)
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\4&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}0&{2\sqrt 3 }\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;0; 8\sqrt 3 } \right)\)
\(\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 2}\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 1}&{2\sqrt 3 }\\{ - 2}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;4\sqrt 3 ;8\sqrt 3 } \right)\)
Mặt phẳng (ABC) có một vectơ pháp tuyến là: \(\frac{{ 1}}{{8\sqrt 3 }}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0;0;1} \right)\)
Mặt phẳng (A’B’C’) có một vectơ pháp tuyến là: \(\frac{1}{{4\sqrt 3 }}\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {0;1;2} \right)\)
Do đó, \(\cos \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = \frac{{\left| {0.0 + 0.1 + 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {1^2} + {2^2}} }} = \frac{{2\sqrt 5 }}{5}\)
\( \Rightarrow \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) \approx 26,{6^o}\)
Vậy mái nhà nghiêng so với mặt sàn nhà một góc khoảng \(26,{1^o}\).
Giải mục 3 trang 52,53 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 3 trang 52,53 SGK Toán 12 tập 2 - Kết nối tri thức thường xoay quanh các chủ đề về Đường thẳng và Mặt phẳng trong không gian, cụ thể là việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, góc giữa đường thẳng và mặt phẳng, và khoảng cách từ một điểm đến mặt phẳng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các bài toán hình học không gian phức tạp hơn.
Nội dung chính của Mục 3
- Vị trí tương đối giữa đường thẳng và mặt phẳng: Đường thẳng có thể nằm trong mặt phẳng, song song với mặt phẳng, hoặc cắt mặt phẳng.
- Góc giữa đường thẳng và mặt phẳng: Định nghĩa và cách tính góc giữa đường thẳng và mặt phẳng.
- Khoảng cách từ một điểm đến mặt phẳng: Công thức tính khoảng cách và các ứng dụng.
Hướng dẫn giải chi tiết các bài tập trong Mục 3
Để giải các bài tập trong mục này, bạn cần nắm vững các kiến thức sau:
- Tìm vectơ pháp tuyến của mặt phẳng: Vectơ pháp tuyến đóng vai trò quan trọng trong việc xác định phương trình mặt phẳng và tính góc.
- Tìm vectơ chỉ phương của đường thẳng: Vectơ chỉ phương giúp xác định hướng của đường thẳng.
- Sử dụng tích vô hướng: Tích vô hướng được sử dụng để tính góc giữa hai vectơ và xác định vị trí tương đối giữa đường thẳng và mặt phẳng.
- Áp dụng công thức tính khoảng cách: Sử dụng công thức để tính khoảng cách từ một điểm đến mặt phẳng.
Ví dụ minh họa: Bài tập 1 (trang 52)
Đề bài: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa d và (P).
Giải:
Vectơ chỉ phương của d là a = (1, -1, 2). Vectơ pháp tuyến của (P) là n = (2, -1, 1).
Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 5 ≠ 0. Do đó, đường thẳng d cắt mặt phẳng (P).
Bài tập rèn luyện thêm
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
- Bài tập 2, 3, 4 trang 52, 53 SGK Toán 12 tập 2 - Kết nối tri thức.
- Các bài tập tương tự trong các đề thi thử THPT Quốc gia.
Lưu ý khi giải bài tập
Khi giải các bài tập về đường thẳng và mặt phẳng, bạn cần chú ý:
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Kiểm tra lại các phép tính để tránh sai sót.
- Sử dụng các công thức một cách chính xác.
Tusach.vn hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các bạn học sinh sẽ tự tin hơn trong việc học tập môn Toán 12. Chúc các bạn học tốt!
| Chủ đề | Nội dung |
|---|---|
| Vị trí tương đối | Nằm trong, song song, cắt |
| Góc giữa đường thẳng và mặt phẳng | Công thức tính, điều kiện |
| Khoảng cách | Công thức, ứng dụng |