Giải mục 3 trang 33,34,35 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 3 trang 33,34,35 SGK Toán 12 tập 2 - Kết nối tri thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 2 - Kết nối tri thức. Mục 3 trang 33,34,35 tập trung vào các kiến thức quan trọng về...
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của tusach.vn đã biên soạn lời giải chi tiết, dễ hiểu, giúp bạn tự tin giải quyết mọi bài tập.
Lập phương trình tổng quát của mặt phẳng
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 33 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\).
Dựa vào HĐ4, hãy nêu phương trình của \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình tổng quát của mặt phẳng để giải: Trong không gian Oxyz, mỗi phương trình \(Ax + By + Cz + D = 0\) (các hệ số A, B, C không đồng thời bằng 0) xác định một mặt phẳng nhận \(\overrightarrow n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến.
Lời giải chi tiết:
Gọi điểm M(x; y; z) thuộc \(\left( \alpha \right)\). Khi đó, hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
Ta có: \(\overrightarrow {{M_o}M} \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)
Suy ra phương trình của \(\left( \alpha \right)\) là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
\( \Leftrightarrow Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\)
Vậy phương trình của \(\left( \alpha \right)\) là: \(Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\)
LT6
Trả lời câu hỏi Luyện tập 6 trang 33 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) và vuông góc với trục Oz.
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến để viết phương trình: Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\) thì có phương trình là:
\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0 \Leftrightarrow Ax + By + Cz + D = 0\) với \(D = - \left( {A{x_0} + B{y_0} + C{z_0}} \right)\)
Lời giải chi tiết:
Vì mặt phẳng \(\left( \alpha \right)\) vuông góc với trục Oz nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n \left( {0;0;1} \right)\) làm một vectơ pháp tuyến. Mà mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) nên phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\) là: \(0\left( {x - 1} \right) + 0\left( {y - 2} \right) + 1.\left( {z + 4} \right) = 0 \Leftrightarrow z + 4 = 0\)
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 33 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và biết cặp vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow v = \left( {a';b';c'} \right)\).
a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
b) Viết phương trình mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến để viết phương trình: Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\) thì có phương trình là:
\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0 \Leftrightarrow Ax + By + Cz + D = 0\) với \(D = A{x_0} - B{y_0} - C{y_0}\)
Lời giải chi tiết:
a) Vì \(\overrightarrow u ,\overrightarrow v \) là các vectơ chỉ phương của mặt phẳng \(\left( \alpha \right)\). Do đó, \(\overrightarrow u ,\overrightarrow v \) cùng vuông góc với vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) là: \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\).
b) Vì mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\) và đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) nên phương trình mặt phẳng \(\left( \alpha \right)\) là:
\(\left( {bc' - b'c} \right)\left( {x - {x_0}} \right) + \left( {ca' - c'a} \right)\left( {y - {y_0}} \right) + \left( {ab' - a'b} \right)\left( {z - {z_0}} \right) = 0\)
LT7
Trả lời câu hỏi Luyện tập 7 trang 343 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2; - 1} \right),B\left( {4;1;2} \right),C\left( {2;3;1} \right)\). Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC.
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau:
+ Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến\(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
Trục Oy có một vectơ chỉ phương là: \(\overrightarrow j = \left( {0;1;0} \right)\).
Đường thẳng BC có một vectơ chỉ phương là: \(\overrightarrow {BC} \left( { - 2;2; - 1} \right)\).
Vì mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right]\) làm một vectơ pháp tuyến.
\(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\0&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&2\\0&1\end{array}} \right|} \right) = \left( {1;0; - 2} \right)\)
Do đó, phương trình mặt phẳng \(\left( \alpha \right)\) là: \(1\left( {x - 1} \right) - 2\left( {z + 1} \right) = 0 \Leftrightarrow x - 2z - 3 = 0\)
HĐ7
Trả lời câu hỏi Hoạt động 7 trang 34 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1;2;3} \right),B\left( { - 1;3;4} \right),C\left( {2; - 1;2} \right)\)
a) Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC).
b) Viết phương trình mặt phẳng (ABC).
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau:
+ Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
a) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\).
b) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&1\\{ - 3}&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&1\\1&{ - 3}\end{array}} \right|} \right) = \left( {2; - 1;5} \right)\)
Mặt phẳng (ABC) đi qua điểm \(A\left( {1;2;3} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 1;5} \right)\) nên phương trình mặt phẳng (ABC) là: \(2\left( {x - 1} \right) - \left( {y - 2} \right) + 5\left( {z - 3} \right) = 0 \Leftrightarrow 2x - y + 5z - 15 = 0\).
VD2
Trả lời câu hỏi Vận dụng 2 trang 35 SGK Toán 12 Kết nối tri thức
Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.
a) Xác định tọa độ của vị trí \({M_1},{M_2},{M_3}\) của vật tương ứng với các thời điểm \(t = 0,t = \frac{\pi }{2},t = \pi \).
b) Chứng minh rằng \({M_1},{M_2},{M_3}\) không thẳng hàng và viết phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\).
c) Vị trí \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) có luôn thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) hay không?
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
+ Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \)
+ Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \).
Lời giải chi tiết:
a) Với \(t = 0\) ta có: \({M_1}\left( {1;1;1} \right)\)
Với \(t = \frac{\pi }{2}\) ta có: \({M_2}\left( { - 1;1;0} \right)\)
Với \(t = \pi \) ta có: \({M_3}\left( { - 1; - 1; - 1} \right)\)
b) Hai vectơ \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) không cùng phương nên ba điểm \({M_1},{M_2},{M_3}\) không thẳng hàng.
c) Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 1}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&0\\{ - 2}&{ - 2}\end{array}} \right|} \right) = \left( { - 2; - 2;4} \right)\)
Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có vectơ pháp tuyến \(\overrightarrow n \left( { - 2; - 2;4} \right)\) và đi qua điểm \({M_2}\left( { - 1;1;0} \right)\) nên phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) là:
\( - 2\left( {x + 1} \right) - 2\left( {y - 1} \right) + 4z = 0 \Leftrightarrow x + 1 + y - 1 - 2z = 0 \Leftrightarrow x + y - 2z = 0\) (1)
c) Với \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thay vào (1) ta có:
$\cos t-\sin t+\cos t+\sin t-2\cos t=0\Leftrightarrow 0=0\left( L D\right)$
Vậy \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\). Do đó, vật thể M luôn chuyển động trong một mặt phẳng cố định.
LT8
Trả lời câu hỏi Luyện tập 8 trang 35 SGK Toán 12 Kết nối tri thức
(H.5.8) Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) \(\left( {a,b,c \ne 0} \right)\).
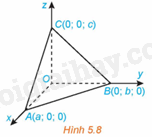
Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (Phương trình trên được gọi là phương trình mặt phẳng theo đoạn chắn).
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
+ Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \)
+ Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \).
Lời giải chi tiết:
Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - a;b;0} \right),\overrightarrow {AC} \left( { - a;0;c} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}b&0\\0&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - a}\\c&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - a}&b\\{ - a}&0\end{array}} \right|} \right) = \left( {bc;ac;ab} \right)\)
Mặt phẳng (ABC) đi qua điểm A(a; 0; 0) và vectơ pháp tuyến \(\overrightarrow n = \left( {bc;ac;ab} \right)\) nên phương trình mặt phẳng (ABC) là:
\(bc\left( {x - a} \right) + acy + abz = 0 \Leftrightarrow bcx + acy + abz = bca \Leftrightarrow \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (đpcm)
- HĐ5
- LT6
- HĐ6
- LT7
- HĐ7
- LT8
- VD2
Trả lời câu hỏi Hoạt động 5 trang 33 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\).
Dựa vào HĐ4, hãy nêu phương trình của \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình tổng quát của mặt phẳng để giải: Trong không gian Oxyz, mỗi phương trình \(Ax + By + Cz + D = 0\) (các hệ số A, B, C không đồng thời bằng 0) xác định một mặt phẳng nhận \(\overrightarrow n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến.
Lời giải chi tiết:
Gọi điểm M(x; y; z) thuộc \(\left( \alpha \right)\). Khi đó, hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
Ta có: \(\overrightarrow {{M_o}M} \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)
Suy ra phương trình của \(\left( \alpha \right)\) là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
\( \Leftrightarrow Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\)
Vậy phương trình của \(\left( \alpha \right)\) là: \(Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\)
Trả lời câu hỏi Luyện tập 6 trang 33 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) và vuông góc với trục Oz.
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến để viết phương trình: Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\) thì có phương trình là:
\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0 \Leftrightarrow Ax + By + Cz + D = 0\) với \(D = - \left( {A{x_0} + B{y_0} + C{z_0}} \right)\)
Lời giải chi tiết:
Vì mặt phẳng \(\left( \alpha \right)\) vuông góc với trục Oz nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n \left( {0;0;1} \right)\) làm một vectơ pháp tuyến. Mà mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) nên phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\) là: \(0\left( {x - 1} \right) + 0\left( {y - 2} \right) + 1.\left( {z + 4} \right) = 0 \Leftrightarrow z + 4 = 0\)
Trả lời câu hỏi Hoạt động 6 trang 33 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và biết cặp vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow v = \left( {a';b';c'} \right)\).
a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
b) Viết phương trình mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến để viết phương trình: Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\) thì có phương trình là:
\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0 \Leftrightarrow Ax + By + Cz + D = 0\) với \(D = A{x_0} - B{y_0} - C{y_0}\)
Lời giải chi tiết:
a) Vì \(\overrightarrow u ,\overrightarrow v \) là các vectơ chỉ phương của mặt phẳng \(\left( \alpha \right)\). Do đó, \(\overrightarrow u ,\overrightarrow v \) cùng vuông góc với vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) là: \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\).
b) Vì mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\) và đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) nên phương trình mặt phẳng \(\left( \alpha \right)\) là:
\(\left( {bc' - b'c} \right)\left( {x - {x_0}} \right) + \left( {ca' - c'a} \right)\left( {y - {y_0}} \right) + \left( {ab' - a'b} \right)\left( {z - {z_0}} \right) = 0\)
Trả lời câu hỏi Luyện tập 7 trang 343 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2; - 1} \right),B\left( {4;1;2} \right),C\left( {2;3;1} \right)\). Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC.
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau:
+ Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến\(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
Trục Oy có một vectơ chỉ phương là: \(\overrightarrow j = \left( {0;1;0} \right)\).
Đường thẳng BC có một vectơ chỉ phương là: \(\overrightarrow {BC} \left( { - 2;2; - 1} \right)\).
Vì mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right]\) làm một vectơ pháp tuyến.
\(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\0&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&2\\0&1\end{array}} \right|} \right) = \left( {1;0; - 2} \right)\)
Do đó, phương trình mặt phẳng \(\left( \alpha \right)\) là: \(1\left( {x - 1} \right) - 2\left( {z + 1} \right) = 0 \Leftrightarrow x - 2z - 3 = 0\)
Trả lời câu hỏi Hoạt động 7 trang 34 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1;2;3} \right),B\left( { - 1;3;4} \right),C\left( {2; - 1;2} \right)\)
a) Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC).
b) Viết phương trình mặt phẳng (ABC).
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau:
+ Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
a) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\).
b) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&1\\{ - 3}&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&1\\1&{ - 3}\end{array}} \right|} \right) = \left( {2; - 1;5} \right)\)
Mặt phẳng (ABC) đi qua điểm \(A\left( {1;2;3} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 1;5} \right)\) nên phương trình mặt phẳng (ABC) là: \(2\left( {x - 1} \right) - \left( {y - 2} \right) + 5\left( {z - 3} \right) = 0 \Leftrightarrow 2x - y + 5z - 15 = 0\).
Trả lời câu hỏi Luyện tập 8 trang 35 SGK Toán 12 Kết nối tri thức
(H.5.8) Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) \(\left( {a,b,c \ne 0} \right)\).
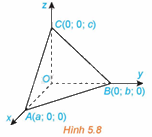
Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (Phương trình trên được gọi là phương trình mặt phẳng theo đoạn chắn).
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
+ Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \)
+ Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \).
Lời giải chi tiết:
Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - a;b;0} \right),\overrightarrow {AC} \left( { - a;0;c} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}b&0\\0&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - a}\\c&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - a}&b\\{ - a}&0\end{array}} \right|} \right) = \left( {bc;ac;ab} \right)\)
Mặt phẳng (ABC) đi qua điểm A(a; 0; 0) và vectơ pháp tuyến \(\overrightarrow n = \left( {bc;ac;ab} \right)\) nên phương trình mặt phẳng (ABC) là:
\(bc\left( {x - a} \right) + acy + abz = 0 \Leftrightarrow bcx + acy + abz = bca \Leftrightarrow \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (đpcm)
Trả lời câu hỏi Vận dụng 2 trang 35 SGK Toán 12 Kết nối tri thức
Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.
a) Xác định tọa độ của vị trí \({M_1},{M_2},{M_3}\) của vật tương ứng với các thời điểm \(t = 0,t = \frac{\pi }{2},t = \pi \).
b) Chứng minh rằng \({M_1},{M_2},{M_3}\) không thẳng hàng và viết phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\).
c) Vị trí \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) có luôn thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) hay không?
Phương pháp giải:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
+ Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \)
+ Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \).
Lời giải chi tiết:
a) Với \(t = 0\) ta có: \({M_1}\left( {1;1;1} \right)\)
Với \(t = \frac{\pi }{2}\) ta có: \({M_2}\left( { - 1;1;0} \right)\)
Với \(t = \pi \) ta có: \({M_3}\left( { - 1; - 1; - 1} \right)\)
b) Hai vectơ \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) không cùng phương nên ba điểm \({M_1},{M_2},{M_3}\) không thẳng hàng.
c) Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 1}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&0\\{ - 2}&{ - 2}\end{array}} \right|} \right) = \left( { - 2; - 2;4} \right)\)
Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có vectơ pháp tuyến \(\overrightarrow n \left( { - 2; - 2;4} \right)\) và đi qua điểm \({M_2}\left( { - 1;1;0} \right)\) nên phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) là:
\( - 2\left( {x + 1} \right) - 2\left( {y - 1} \right) + 4z = 0 \Leftrightarrow x + 1 + y - 1 - 2z = 0 \Leftrightarrow x + y - 2z = 0\) (1)
c) Với \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thay vào (1) ta có:
$\cos t-\sin t+\cos t+\sin t-2\cos t=0\Leftrightarrow 0=0\left( L D\right)$
Vậy \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\). Do đó, vật thể M luôn chuyển động trong một mặt phẳng cố định.
Giải mục 3 trang 33,34,35 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 3 trong SGK Toán 12 tập 2 - Kết nối tri thức thường xoay quanh các chủ đề về Đường thẳng và Mặt phẳng trong không gian, bao gồm các kiến thức về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng, và khoảng cách từ một điểm đến mặt phẳng. Việc nắm vững các khái niệm và định lý trong mục này là vô cùng quan trọng để giải quyết các bài toán hình học không gian một cách hiệu quả.
Nội dung chính của Mục 3 trang 33,34,35
- Định lý về đường thẳng vuông góc với mặt phẳng: Nghiên cứu các điều kiện để một đường thẳng vuông góc với một mặt phẳng và các tính chất liên quan.
- Định lý về hai mặt phẳng vuông góc: Tìm hiểu các điều kiện để hai mặt phẳng vuông góc và các hệ quả của định lý này.
- Góc giữa hai mặt phẳng: Cách xác định và tính toán góc giữa hai mặt phẳng.
- Khoảng cách từ một điểm đến mặt phẳng: Công thức tính khoảng cách và các ứng dụng của nó.
Phương pháp giải bài tập hiệu quả
Để giải tốt các bài tập trong Mục 3, bạn cần:
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, định lý và tính chất liên quan.
- Vẽ hình: Vẽ hình chính xác và trực quan để hình dung rõ bài toán.
- Sử dụng các công thức: Áp dụng các công thức một cách linh hoạt và chính xác.
- Phân tích bài toán: Xác định các yếu tố đã cho và yếu tố cần tìm.
- Kiểm tra lại kết quả: Đảm bảo kết quả cuối cùng hợp lý và phù hợp với điều kiện của bài toán.
Giải chi tiết các bài tập trang 33, 34, 35
Dưới đây là giải chi tiết các bài tập trong Mục 3 trang 33, 34, 35 SGK Toán 12 tập 2 - Kết nối tri thức:
Bài 1: (Trang 33)
(Nội dung bài tập và lời giải chi tiết)
Bài 2: (Trang 34)
(Nội dung bài tập và lời giải chi tiết)
Bài 3: (Trang 35)
(Nội dung bài tập và lời giải chi tiết)
Ví dụ minh họa
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Giải:
- Gọi O là giao điểm của AC và BD.
- Vì SA vuông góc với (ABCD) nên SA vuông góc với OC.
- Tam giác SOC vuông tại O, suy ra góc SCO là góc giữa SC và mặt phẳng (ABCD).
- Tính SO = √(SA² + AO²) = √(a² + (a√2/2)²) = a√(3/2).
- tan SCO = SO/OC = (a√(3/2))/(a√2/2) = √3.
- Suy ra SCO = 60°.
Lưu ý quan trọng
Khi giải các bài tập về đường thẳng và mặt phẳng, hãy chú ý đến các trường hợp đặc biệt và sử dụng các tính chất đối xứng để đơn giản hóa bài toán. Ngoài ra, việc luyện tập thường xuyên với nhiều dạng bài tập khác nhau sẽ giúp bạn nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả này, bạn sẽ tự tin chinh phục các bài tập trong Mục 3 trang 33,34,35 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc bạn học tốt!