Giải bài tập 3.2 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 3.2 Trang 79 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3.2 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau: Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Đề bài
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
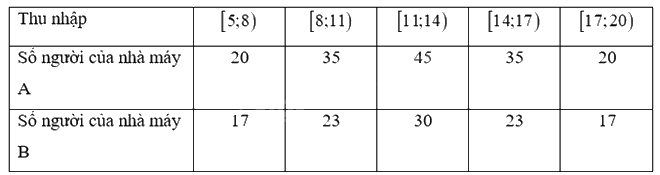
Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng biến thiên của mẫu số liệu ghép nhóm để tính:
Cho mẫu số liệu ghép nhóm:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = {a_{k + 1}} - {a_1}\).
+ Sử dụng kiến thức về khoảng tứ phân vị của mẫu số liệu ghép nhóm để tính: Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Lời giải chi tiết
Ta có bảng số liệu với giá trị đại diện của nhóm là:
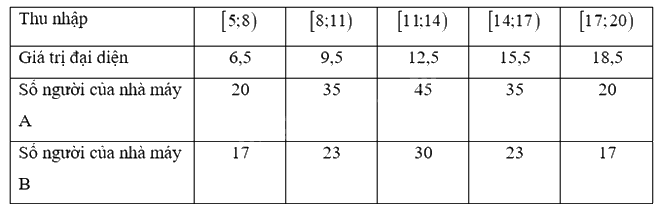
Mức thu nhập trung bình của người lao động nhà máy A là:
\(\frac{{6,5.20 + 9,5.35 + 12,5.45 + 15,5.35 + 18,5.20}}{{20 + 35 + 45 + 35 + 20}} = \frac{{25}}{2}\) (triệu đồng)
Mức thu nhập trung bình của người lao động nhà máy B là:
\(\frac{{6,5.17 + 9,5.23 + 12,5.30 + 15,5.23 + 18,5.17}}{{17 + 23 + 30 + 23 + 17}} = \frac{{25}}{2}\) (triệu đồng)
Nhà máy A: Ta có cỡ mẫu \(n = 155\). Giả sử \({x_1},{x_2},...,{x_{155}}\) là mức thu nhập của người lao động nhà máy A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì \(\frac{n}{4} = 38,75\) và \(20 < 38,75 < 20 + 35\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ {8;11} \right)\) và tứ phân vị thứ nhất là: \({Q_1} = 8 + \frac{{\frac{{155}}{4} - 20}}{{35}}.3 = \frac{{269}}{{28}}\)
Vì \(\frac{{3n}}{4} = 116,25\) và \(20 + 35 + 45 < 116,25 < 20 + 35 + 45 + 35\) nên nhóm chứa tứ phân vị thứ ba là nhóm \(\left[ {14;17} \right)\) và tứ phân vị thứ ba là: \({Q_3} = 14 + \frac{{\frac{{3.155}}{4} - \left( {20 + 35 + 45} \right)}}{{35}}.3 = \frac{{431}}{{28}}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \({\Delta _{{Q_1}}} = \frac{{431}}{{28}} - \frac{{269}}{{28}} = \frac{{81}}{{14}}\)
Nhà máy B: Ta có cỡ mẫu \(n = 110\). Giả sử \({x_1},{x_2},...,{x_{110}}\) là mức thu nhập của người lao động nhà máy B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì \(\frac{n}{4} = 27,5\) và \(17 < 27,5 < 17 + 23\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ {8;11} \right)\) và tứ phân vị thứ nhất là: \(Q{'_1} = 8 + \frac{{\frac{{110}}{4} - 17}}{{23}}.3 = \frac{{431}}{{46}}\)
Vì \(\frac{{3n}}{4} = 82,5\) và \(17 + 23 + 30 < 82,5 < 17 + 23 + 30 + 23\) nên nhóm chứa tứ phân vị thứ ba là nhóm \(\left[ {14;17} \right)\) và tứ phân vị thứ ba là: \({Q_3} = 14 + \frac{{\frac{{3.110}}{4} - \left( {17 + 23 + 30} \right)}}{{23}}.3 = \frac{{719}}{{46}}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \({\Delta _{{Q_2}}} = \frac{{719}}{{46}} - \frac{{431}}{{46}} = \frac{{144}}{{23}}\)
Vì \({\Delta _{{Q_1}}} < {\Delta _{{Q_2}}}\) nên mức thu nhập của người lao động nhà máy B biến động nhiều hơn.
Giải Bài Tập 3.2 Trang 79 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 3.2 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Nội Dung Bài Tập 3.2
Thông thường, bài tập 3.2 sẽ yêu cầu:
- Tính đạo hàm của một hàm số cho trước.
- Tìm đạo hàm cấp hai của một hàm số.
- Xác định các điểm cực trị của hàm số.
- Khảo sát sự biến thiên của hàm số.
- Giải các bài toán liên quan đến ứng dụng của đạo hàm (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số).
Phương Pháp Giải Bài Tập 3.2
Để giải quyết bài tập 3.2 một cách hiệu quả, các em cần nắm vững các bước sau:
- Xác định đúng công thức đạo hàm cần sử dụng: Tùy thuộc vào dạng hàm số, các em cần chọn công thức đạo hàm phù hợp (ví dụ: đạo hàm của hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Áp dụng quy tắc tính đạo hàm: Sử dụng các quy tắc như quy tắc tích, quy tắc thương, quy tắc chuỗi để tính đạo hàm của các hàm số phức tạp.
- Giải phương trình đạo hàm: Để tìm các điểm cực trị, các em cần giải phương trình đạo hàm bằng 0.
- Khảo sát dấu của đạo hàm: Xác định dấu của đạo hàm trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
- Kết luận: Đưa ra kết luận về các điểm cực trị, khoảng đồng biến, nghịch biến, và giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Ví Dụ Minh Họa
Giả sử bài tập 3.2 yêu cầu tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1.
Giải:
f'(x) = 3x2 - 6x + 2
Lưu Ý Quan Trọng
- Luôn kiểm tra lại kết quả tính đạo hàm để đảm bảo tính chính xác.
- Hiểu rõ ý nghĩa của đạo hàm trong việc khảo sát hàm số.
- Luyện tập thường xuyên để nắm vững các kỹ năng giải bài tập.
Tusach.vn - Nguồn Tài Liệu Toán Học Uy Tín
Tusach.vn là một trang web cung cấp đầy đủ các tài liệu học tập môn Toán, bao gồm SGK, SBT, đề thi, và lời giải chi tiết. Chúng tôi luôn cập nhật những thông tin mới nhất và hữu ích nhất để giúp các em học tập tốt hơn.
Hy vọng bài viết này đã giúp các em hiểu rõ cách giải bài tập 3.2 trang 79 SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| (xn)' = nxn-1 | Đạo hàm của hàm lũy thừa |
| (sin x)' = cos x | Đạo hàm của hàm sin |
| (cos x)' = -sin x | Đạo hàm của hàm cos |