Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 2.39 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức
SGK Toán 12 - Kết nối tri thức
Giải Toán 12 tập 1 - Kết nối tri thức
Chương 2. Vectơ và hệ trục tọa độ trong không gian
Bài tập cuối chương 2

Giải bài tập 2.39 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức

Giải Bài Tập 2.39 Trang 74 Toán 12 Tập 1 - Kết Nối Tri Thức

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 2.39 trang 74 một cách dễ hiểu nhất.

Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm \(A\left( {2;3;1} \right),C\left( { - 1;2;3} \right)\) và \(O'\left( {1; - 2;2} \right)\). Tìm tọa độ các đỉnh còn lại của hình hộp.

Đề bài

Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm \(A\left( {2;3;1} \right),C\left( { - 1;2;3} \right)\) và \(O'\left( {1; - 2;2} \right)\). Tìm tọa độ các đỉnh còn lại của hình hộp.

Phương pháp giải - Xem chi tiếtGiải bài tập 2.39 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức 1

Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm \(A\left( {2;3;1} \right),C\left( { - 1;2;3} \right)\) và \(O'\left( {1; - 2;2} \right)\). Tìm tọa độ các đỉnh còn lại của hình hộp.

Lời giải chi tiết

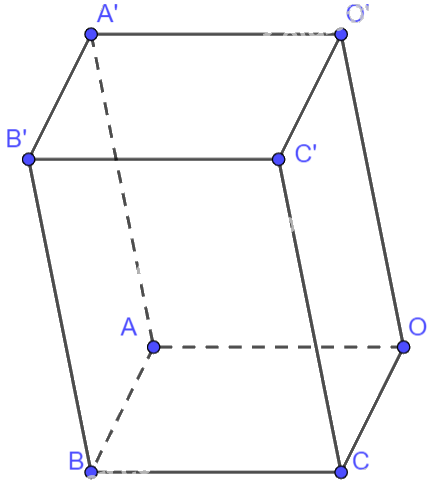
Giải bài tập 2.39 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức 2

Ta có: O(0; 0; 0)

Vì OABC.O’A’B’C’ là hình hộp nên \(\overrightarrow {AA'} = \overrightarrow {OO'} \Rightarrow \left\{ \begin{array}{l}{x_{A'}} - {x_A} = {x_{O'}} - {x_O}\\{y_{A'}} - {y_A} = {y_{O'}} - {y_O}\\{z_{A'}} - {z_A} = {z_{O'}} - {z_O}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_{O'}} - {x_O} + {x_A} = 3\\{y_{A'}} = {y_{O'}} - {y_O} + {y_A} = 1\\{z_{A'}} = {z_{O'}} - {z_O} + {z_A} = 3\end{array} \right. \Rightarrow A'\left( {3;1;3} \right)\)

\(\overrightarrow {CC'} = \overrightarrow {OO'} \Rightarrow \left\{ \begin{array}{l}{x_{C'}} - {x_C} = {x_{O'}} - {x_O}\\{y_{C'}} - {y_C} = {y_{O'}} - {y_O}\\{z_{C'}} - {z_C} = {z_{O'}} - {z_O}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{C'}} = {x_{O'}} - {x_O} + {x_C} = 0\\{y_{C'}} = {y_{O'}} - {y_O} + {y_C} = 0\\{z_{C'}} = {z_{O'}} - {z_O} + {z_C} = 5\end{array} \right. \Rightarrow C'\left( {0;0;5} \right)\)

Vì ABCO là hình bình hành nên \(\overrightarrow {CB} = \overrightarrow {OA} \Rightarrow \left\{ \begin{array}{l}{x_B} + 1 = 2\\{y_B} - 2 = 3\\{z_B} - 3 = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_B} = 1\\{y_B} = 5\\{z_B} = 4\end{array} \right. \Rightarrow B\left( {1;5;4} \right)\)

Vì OABC.O’A’B’C’ là hình hộp nên \(\overrightarrow {BB'} = \overrightarrow {OO'} \Rightarrow \left\{ \begin{array}{l}{x_{B'}} - 1 = 1\\{y_{B'}} - 5 = - 2\\{z_{B'}} - 4 = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{B'}} = 2\\{y_{B'}} = 3\\{z_{B'}} = 6\end{array} \right. \Rightarrow B'\left( {2;3;6} \right)\)

Giải Bài Tập 2.39 Trang 74 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết

Bài tập 2.39 trang 74 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương trình học về đạo hàm. Để giải bài tập này, chúng ta cần nắm vững các kiến thức về:

  • Định nghĩa đạo hàm của hàm số tại một điểm.
  • Các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
  • Đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).

Nội dung bài tập 2.39:

(Đề bài cụ thể của bài tập 2.39 sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) = x3 - 3x + 2. Tính f'(x) và f'(1).)

Lời giải chi tiết:

Để giải bài tập này, chúng ta thực hiện các bước sau:

  1. Bước 1: Tính đạo hàm f'(x)

    2. Sử dụng quy tắc đạo hàm của hàm đa thức, ta có:

    f'(x) = d/dx (x3 - 3x + 2) = 3x2 - 3

  2. Bước 2: Tính f'(1)

    3. Thay x = 1 vào biểu thức f'(x), ta được:

    f'(1) = 3(1)2 - 3 = 3 - 3 = 0

Kết luận:

Vậy, đạo hàm của hàm số f(x) = x3 - 3x + 2 là f'(x) = 3x2 - 3 và f'(1) = 0.

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài tập 2.39, chương này còn nhiều bài tập khác yêu cầu tính đạo hàm. Để giải các bài tập này, bạn cần:

  • Xác định đúng quy tắc đạo hàm cần sử dụng.
  • Thực hiện các phép tính đạo hàm một cách chính xác.
  • Kiểm tra lại kết quả để đảm bảo tính đúng đắn.

Ví dụ về một bài tập tương tự:

(Đề bài bài tập tương tự sẽ được chèn vào đây. Ví dụ: Cho hàm số y = g(x) = 2x2 + 5x - 1. Tính g'(x) và g'(2).)

Hãy tự giải bài tập này để củng cố kiến thức và kỹ năng của bạn.

Lưu ý quan trọng khi giải bài tập về đạo hàm

Khi giải bài tập về đạo hàm, bạn cần chú ý:

  • Nắm vững định nghĩa và các quy tắc tính đạo hàm.
  • Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
  • Sử dụng máy tính bỏ túi để kiểm tra kết quả.

Nếu bạn gặp khó khăn trong quá trình giải bài tập, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ.

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

Tusach.vn luôn cập nhật những lời giải bài tập mới nhất và chính xác nhất, giúp bạn học tập hiệu quả hơn. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!

ChươngBàiLiên kết
11.1Giải bài tập 1.1
11.2Giải bài tập 1.2

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN