Lý Thuyết Tích Phân Toán 12 Kết Nối Tri Thức

Lý thuyết Tích phân Toán 12 Kết nối tri thức

Tích phân là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 12, đặc biệt là với chương trình Kết nối tri thức.

Nắm vững lý thuyết tích phân không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng vững chắc cho các kỳ thi quan trọng như THPT Quốc gia.

Tusach.vn xin giới thiệu tài liệu tổng hợp đầy đủ và chi tiết lý thuyết tích phân Toán 12 Kết nối tri thức, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất.

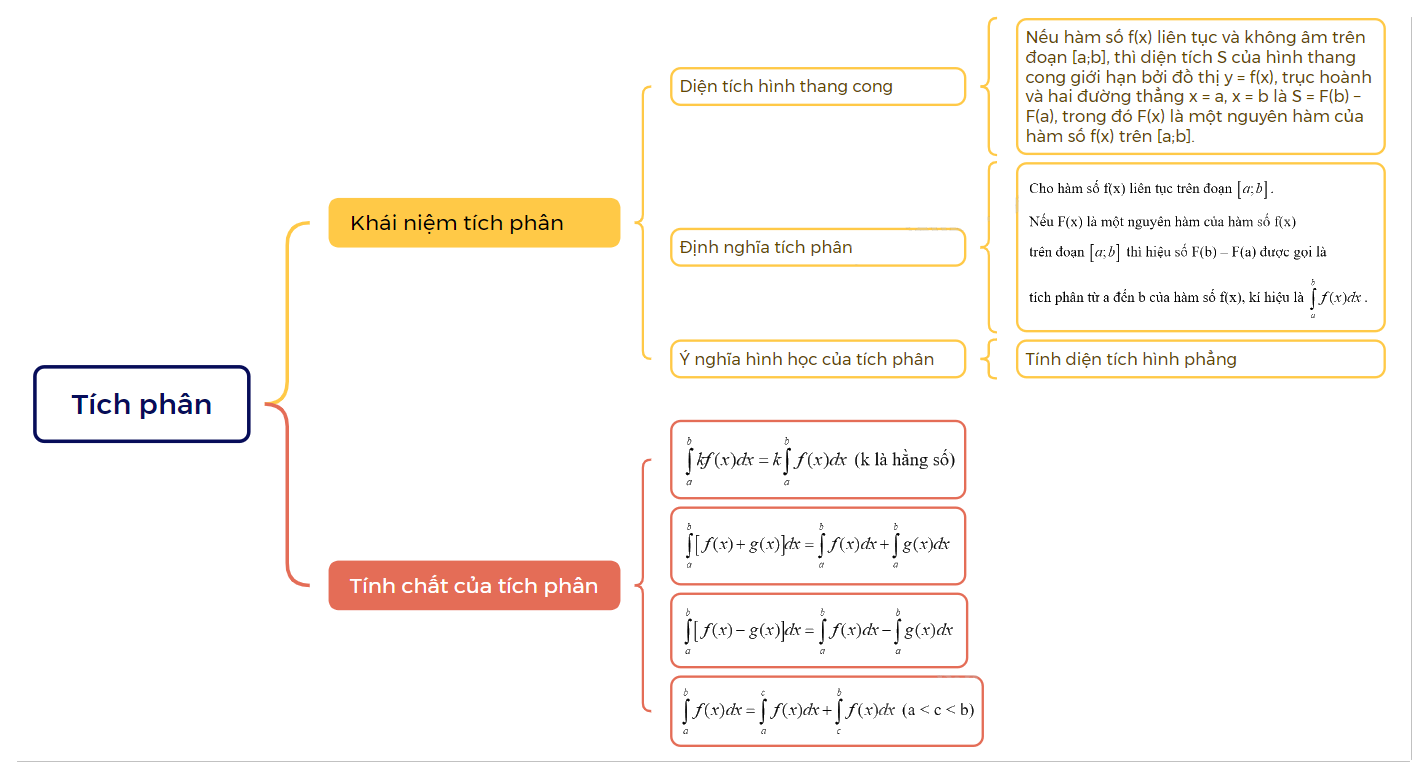
1.Khái niệm tích phân a) Diện tích hình thang cong

1.Khái niệm tích phân

a) Diện tích hình thang cong

Nếu hàm số f(x) liên tục và không âm trên đoạn \(\left[ {a;b} \right]\), thì diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b là S = F(b) – F(a), trong đó F(x) là một nguyên hàm của hàm số f(x) trên \(\left[ {a;b} \right]\).

b) Định nghĩa tích phân

Cho hàm số f(x) liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\) thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là \(\int\limits_a^b {f(x)dx} \).

Ý nghĩa hình học của tích phân:

Nếu hàm số f(x) liên tục và không âm trên đoạn \(\left[ {a;b} \right]\), thì tích phân \(\int\limits_a^b {f(x)dx} \) là diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b.

2. Tính chất của tích phân

\(\int\limits_a^b {kf(x)dx = k\int\limits_a^b {f(x)dx} } \) (k là hằng số)
\(\int\limits_a^b {\left[ {f(x) + g(x)} \right]} dx = \int\limits_a^b {f(x)dx + \int\limits_a^b {g(x)dx} } \)
\(\int\limits_a^b {\left[ {f(x) - g(x)} \right]} dx = \int\limits_a^b {f(x)dx - \int\limits_a^b {g(x)dx} } \)
\(\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx + \int\limits_c^b {f(x)dx} } } \) (a<c<b)

Lý Thuyết Tích Phân Toán 12 Kết Nối Tri Thức: Tổng Quan Chi Tiết

Tích phân là một khái niệm then chốt trong giải tích, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Trong chương trình Toán 12 Kết nối tri thức, tích phân được trình bày một cách hệ thống và logic, giúp học sinh nắm bắt kiến thức một cách dễ dàng. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết tích phân, bao gồm các khái niệm cơ bản, các tính chất quan trọng và các phương pháp tính tích phân thường gặp.

1. Nguyên Hàm và Tích Phân Bất Định

Nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x), tức là F'(x) = f(x). Tích phân bất định của f(x) được ký hiệu là ∫f(x)dx và đại diện cho tập hợp tất cả các nguyên hàm của f(x). Công thức tính tích phân bất định của một số hàm số cơ bản:

∫xⁿdx = (xⁿ⁺¹)/(n+1) + C (n ≠ -1)
∫(1/x)dx = ln|x| + C
∫e^xdx = e^x + C
∫sin(x)dx = -cos(x) + C
∫cos(x)dx = sin(x) + C

Trong đó, C là hằng số tích phân.

2. Tích Phân Xác Định

Tích phân xác định của hàm số f(x) trên đoạn [a, b] được ký hiệu là ∫_a^bf(x)dx và đại diện cho diện tích có dấu giữa đồ thị của hàm số f(x), trục hoành và hai đường thẳng x = a và x = b. Công thức tính tích phân xác định:

∫_a^bf(x)dx = F(b) - F(a), trong đó F(x) là một nguyên hàm của f(x).

3. Các Tính Chất của Tích Phân

Tích phân có một số tính chất quan trọng giúp đơn giản hóa việc tính toán:

∫_a^b[f(x) + g(x)]dx = ∫_a^bf(x)dx + ∫_a^bg(x)dx
∫_a^bkf(x)dx = k∫_a^bf(x)dx (k là hằng số)
∫_a^bf(x)dx = -∫_b^af(x)dx
∫_a^af(x)dx = 0

4. Các Phương Pháp Tính Tích Phân

Có nhiều phương pháp để tính tích phân, tùy thuộc vào dạng của hàm số:

Phương pháp đổi biến số: Sử dụng để đơn giản hóa tích phân bằng cách thay đổi biến số.
Phương pháp tích phân từng phần: Sử dụng để tính tích phân của tích hai hàm số. Công thức: ∫u dv = uv - ∫v du
Phương pháp phân tích thành phân thức đơn giản: Sử dụng để tính tích phân của các hàm số hữu tỉ.

5. Ứng Dụng của Tích Phân

Tích phân có nhiều ứng dụng thực tế, bao gồm:

Tính diện tích: Tính diện tích của các hình phẳng giới hạn bởi đồ thị hàm số.
Tính thể tích: Tính thể tích của các vật thể tròn xoay.
Tính độ dài đường cong: Tính độ dài của một đường cong.
Tính công: Tính công thực hiện bởi một lực.

6. Bài Tập Vận Dụng

Để củng cố kiến thức về lý thuyết tích phân, bạn có thể thực hành giải các bài tập sau:

Tính ∫(x² + 1)dx
Tính ∫₀¹e^xdx
Tính ∫xsin(x)dx (sử dụng phương pháp tích phân từng phần)

Tusach.vn hy vọng bài viết này đã cung cấp cho bạn một cái nhìn toàn diện về lý thuyết tích phân Toán 12 Kết nối tri thức. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!