Giải mục 4 trang 54, 55, 56 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 4 trang 54, 55, 56 SGK Toán 12 tập 1 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 4 trang 54, 55, 56 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và logic.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập tốt nhất để giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Tích vô hướng của hai vectơ trong không gian
CH
Trả lời câu hỏi Câu hỏi trang 55SGK Toán 12 Kết nối tri thức
Xác định góc giữa hai vectơ cùng hướng (và khác \(\overrightarrow 0 \)), góc giữa hai vectơ ngược hướng trong không gian
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}\left( {{0^0} \le \widehat {AOB} \le {{180}^0}} \right)\) được gọi là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Góc giữa hai vectơ cùng hướng bằng \({0^0}\).
Góc giữa hai vectơ ngược hướng bằng \({180^0}\).
HD8
Trả lời câu hỏi Hoạt động 8 trang 56SGK Toán 12 Kết nối tri thức
Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u \cdot \overrightarrow v \), được xác định bởi công thức sau: \(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
Lời giải chi tiết:
Công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u \cdot \overrightarrow v \), được xác định bởi công thức sau:
\(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
LT9
Trả lời câu hỏi Luyện tập 9 trang 56SGK Toán 12 Kết nối tri thức
Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right)\) và \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right)\).
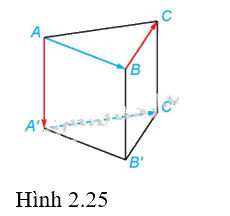
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}\left( {{0^0} \le \widehat {AOB} \le {{180}^0}} \right)\) được gọi là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Vì ABC.A’B’C’ là lăng trụ tam giác đều nên AA’B’B là hình chữ nhật. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \). Do đó: \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BB'} ,\overrightarrow {BC} } \right) = \widehat {B'BC} = {90^0}\) (do BB’C’C là hình chữ nhật)
Vì AA’B’B là hình chữ nhật nên \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right) = \widehat {C'A'B'}\).
Vì tam giác A’B’C’ là tam giác đều nên \(\widehat {C'A'B'} = {60^0}\). Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = {60^0}\).
VD4
Trả lời câu hỏi Vận dụng 4 trang 57SGK Toán 12 Kết nối tri thức
Như đã biết, nếu có một lực \(\overrightarrow F \) tác động vào một vật tại điểm M và làm cho vật đó di chuyển một quãng đường MN thì công A sinh ra được tính theo công thức \(A = \overrightarrow F .\overrightarrow {MN} \), trong đó lực F có độ lớn tính bằng Newton, quãng đường MN tính bằng mét và công A tính bằng Jun (H.2.28). Do đó, nếu dùng một lực \(\overrightarrow F \) có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao. Kết quả trên có thể được áp dụng như thế nào khi kéo (hoặc đẩy) các vật nặng?

Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để giải thích: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hương của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Ta có: \(A = \overrightarrow F .\overrightarrow {MN} = \left| {\overrightarrow F } \right|.\left| {\overrightarrow {MN} } \right|.\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right)\)
Vì lực \(\overrightarrow F \) có độ lớn không đổi và vật di chuyển một quãng đường không đổi nên A lớn nhất khi \(\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right)\) lớn nhất. Do đó, \(\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right) = 1 \Leftrightarrow \left( {\overrightarrow F ,\overrightarrow {MN} } \right) = {0^0}\) . Khi đó, lực tác động cùng hướng với chuyển động của vật. Vậy công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật.
Khi kéo (hoặc đẩy) các vật nặng, ta nên kéo (hoặc đẩy) cùng cùng hướng với chuyển động của vật.
HĐ7
Trả lời câu hỏi Hoạt động 7 trang 54SGK Toán 12 Kết nối tri thức
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy điểm O và vẽ các vectơ\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Lấy điểm O’ khác O và vẽ các vectơ \(\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \) (H.2.21).

a) Hãy giải thích vì sao \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
b) Áp dụng định lí côsin cho hai tam giác OAB và O’A’B’ để giải thích vì sao \(\widehat {AOB} = \widehat {A'O'B'}\)
Phương pháp giải:
a) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
b) Sử dụng kiến thức về định lí côsin để chứng minh: Cho tam giác ABC có, khi đó, \(\cos \widehat A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} ;\overrightarrow {A'B'} = \overrightarrow {A'O'} + \overrightarrow {O'B'} \)
Mà \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \Rightarrow \overrightarrow {AO} = \overrightarrow {A'O'} ;\overrightarrow {OB} = \overrightarrow {O'B'} \)
Do đó, \(\overrightarrow {AB} = \overrightarrow {A'B'} \)
b) Áp dụng định lí côsin vào tam giác AOB ta có: \(\cos \widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Áp dụng định lí côsin vào tam giác A’O’B’ ta có: \(\cos \widehat {A'O'B'} = \frac{{O'A{'^2} + O'B{'^2} - A'B{'^2}}}{{2.O'A'.O'B'}}\)
Vì \(\overrightarrow {AB} = \overrightarrow {A'B'} \Rightarrow AB = A'B',\overrightarrow {AO} = \overrightarrow {A'O'} \Rightarrow OA = O'A';\overrightarrow {OB} = \overrightarrow {O'B'} \Rightarrow OB = O'B'\)
Do đó, \(\cos \widehat {AOB} = \cos \widehat {A'O'B'} \Rightarrow \widehat {AOB} = \widehat {A'O'B'}\)
LT11
Trả lời câu hỏi Luyện tập 11 trang 57SGK Toán 12 Kết nối tri thức
Cho hình lập phương ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 0\).
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Sử dụng kiến thức về tích vô hướng của hai vectơ trong không gian để tính: Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Khi đó, \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \cdot \overrightarrow b = 0\)
Lời giải chi tiết:
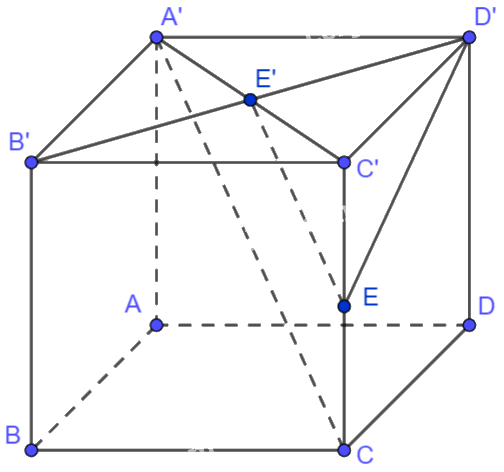
Giả sử cạnh của hình lập phương ABCD.A’B’C’D’ bằng 1. Khi đó, \(A'C' = B'D' = \sqrt 2 \)
Gọi E’ là giao điểm của hai đường chéo A’C’ và B’D’ của hình vuông A’B’C’D’. Khi đó, E’ là trung điểm của A’C’ và B’D’. Suy ra \(\overrightarrow {B'D'} = 2\overrightarrow {E'D'} \) và \(E'D' = \frac{{\sqrt 2 }}{2}\).
Gọi E là trung điểm của CC’. Mà E’ là trung điểm của A’C’ nên EE’ là đường trung bình của tam giác A’C’C. Do đó, \(\overrightarrow {A'C} = 2\overrightarrow {E'E} \) và \(E'E = \frac{1}{2}A'C\)
Áp dụng định lí Pythagore vào \(\Delta \)A’C’C vuông tại C’ có: \(A'C = \sqrt {A'C{'^2} + C'{C^2}} = \sqrt {2 + 1} = \sqrt 3 \)\( \Rightarrow E'E = \frac{{\sqrt 3 }}{2}\)
Áp dụng định lí Pythagore vào \(\Delta \)D’C’E vuông tại C’ có:
\(ED{'^2} = C'D{'^2} + C'{E^2} = 1 + \frac{1}{4} = \frac{5}{4}\)
Vì \(E'D{'^2} + E'{E^2} = \frac{1}{2} + \frac{3}{4} = \frac{5}{4} = ED{'^2}\) nên \(\Delta \)E’D’E vuông tại E’. Do đó, \(\overrightarrow {E'E} \bot \overrightarrow {E'D'} \)
Ta có: \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 2.\overrightarrow {E'E} .2.\overrightarrow {E'D'} \)\( = 0\) (đpcm)
LT10
Trả lời câu hỏi Luyện tập 10 trang 57SGK Toán 12 Kết nối tri thức
Trong Ví dụ 10, hãy tính các tích vô hướng \(\overrightarrow {AS} .\overrightarrow {BD} \) và \(\overrightarrow {AS} .\overrightarrow {CD} \)
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Sử dụng kiến thức về tích vô hướng của hai vectơ trong không gian để tính: Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Khi đó, \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \cdot \overrightarrow b = 0\)
Lời giải chi tiết:
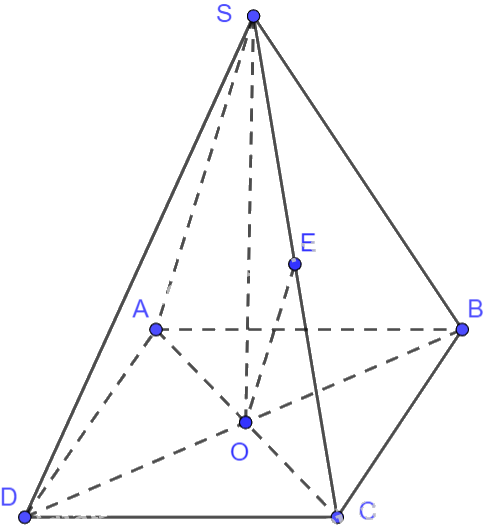
Gọi O là giao điểm của hai đường chéo AC và BD trong hình vuông ABCD. Do đó, O là trung điểm của BD, O là trung điểm của AC.
Tứ giác ABCD là hình vuông cạnh a nên độ dài đường chéo BD là \(a\sqrt 2 \)\( \Rightarrow OB = \frac{{a\sqrt 2 }}{2}\)
Gọi E là trung điểm của SC. Mà O là trung điểm của AC nên OE là đường trung bình của tam giác SAC, do đó, OE//SA, \(OE = \frac{1}{2}SA = \frac{a}{2}\). Suy ra: \(\overrightarrow {AS} = 2\overrightarrow {OE} \)
Vì O là trung điểm của BD nên \(\overrightarrow {BD} = 2\overrightarrow {OB} \)
Vì tam giác SBC có ba cạnh bằng nhau nên tam giác SBC là tam giác đều. Do đó, BE là đường trung tuyến đồng thời là đường cao của tam giác SBC. Do đó, \(EB = \frac{{a\sqrt 3 }}{2}\).
Ta có: \(O{E^2} + O{B^2} = \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} = \frac{{3{a^2}}}{4} = E{B^2}\) nên \(\Delta \)EOB vuông tại O. Do đó, \(\overrightarrow {OE} \bot \overrightarrow {OB} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {BD} = 2\overrightarrow {OE} .\left( { - 2\overrightarrow {OB} } \right) = - 4\overrightarrow {OE} .\overrightarrow {OB} = 0\)
Tứ giác ABCD là hình vuông nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {CD} = \overrightarrow {AS} .\overrightarrow {BA} = - \overrightarrow {AS} .\overrightarrow {AB} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \left( {\overrightarrow {AS} ,\overrightarrow {AB} } \right) = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB}\)
Vì tam giác SAB có ba cạnh bằng nhau nên tam giác SAB đều, suy ra \(\widehat {SAB} = {60^0}\)
Suy ra: \(\overrightarrow {AS} .\overrightarrow {CD} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB} = - a.a.\cos {60^0} = \frac{{ - {a^2}}}{2}\)
- HĐ7
- CH
- LT9
- HD8
- LT10
- LT11
- VD4
Trả lời câu hỏi Hoạt động 7 trang 54SGK Toán 12 Kết nối tri thức
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy điểm O và vẽ các vectơ\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Lấy điểm O’ khác O và vẽ các vectơ \(\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \) (H.2.21).

a) Hãy giải thích vì sao \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
b) Áp dụng định lí côsin cho hai tam giác OAB và O’A’B’ để giải thích vì sao \(\widehat {AOB} = \widehat {A'O'B'}\)
Phương pháp giải:
a) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
b) Sử dụng kiến thức về định lí côsin để chứng minh: Cho tam giác ABC có, khi đó, \(\cos \widehat A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} ;\overrightarrow {A'B'} = \overrightarrow {A'O'} + \overrightarrow {O'B'} \)
Mà \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \Rightarrow \overrightarrow {AO} = \overrightarrow {A'O'} ;\overrightarrow {OB} = \overrightarrow {O'B'} \)
Do đó, \(\overrightarrow {AB} = \overrightarrow {A'B'} \)
b) Áp dụng định lí côsin vào tam giác AOB ta có: \(\cos \widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Áp dụng định lí côsin vào tam giác A’O’B’ ta có: \(\cos \widehat {A'O'B'} = \frac{{O'A{'^2} + O'B{'^2} - A'B{'^2}}}{{2.O'A'.O'B'}}\)
Vì \(\overrightarrow {AB} = \overrightarrow {A'B'} \Rightarrow AB = A'B',\overrightarrow {AO} = \overrightarrow {A'O'} \Rightarrow OA = O'A';\overrightarrow {OB} = \overrightarrow {O'B'} \Rightarrow OB = O'B'\)
Do đó, \(\cos \widehat {AOB} = \cos \widehat {A'O'B'} \Rightarrow \widehat {AOB} = \widehat {A'O'B'}\)
Trả lời câu hỏi Câu hỏi trang 55SGK Toán 12 Kết nối tri thức
Xác định góc giữa hai vectơ cùng hướng (và khác \(\overrightarrow 0 \)), góc giữa hai vectơ ngược hướng trong không gian
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}\left( {{0^0} \le \widehat {AOB} \le {{180}^0}} \right)\) được gọi là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Góc giữa hai vectơ cùng hướng bằng \({0^0}\).
Góc giữa hai vectơ ngược hướng bằng \({180^0}\).
Trả lời câu hỏi Luyện tập 9 trang 56SGK Toán 12 Kết nối tri thức
Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right)\) và \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right)\).
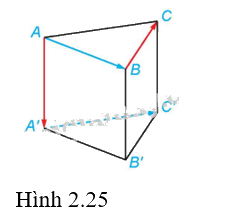
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}\left( {{0^0} \le \widehat {AOB} \le {{180}^0}} \right)\) được gọi là góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Vì ABC.A’B’C’ là lăng trụ tam giác đều nên AA’B’B là hình chữ nhật. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \). Do đó: \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BB'} ,\overrightarrow {BC} } \right) = \widehat {B'BC} = {90^0}\) (do BB’C’C là hình chữ nhật)
Vì AA’B’B là hình chữ nhật nên \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right) = \widehat {C'A'B'}\).
Vì tam giác A’B’C’ là tam giác đều nên \(\widehat {C'A'B'} = {60^0}\). Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = {60^0}\).
Trả lời câu hỏi Hoạt động 8 trang 56SGK Toán 12 Kết nối tri thức
Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u \cdot \overrightarrow v \), được xác định bởi công thức sau: \(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
Lời giải chi tiết:
Công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u \cdot \overrightarrow v \), được xác định bởi công thức sau:
\(\overrightarrow u \cdot \overrightarrow v = \left| {\overrightarrow u } \right| \cdot \left| {\overrightarrow v } \right| \cdot \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
Trả lời câu hỏi Luyện tập 10 trang 57SGK Toán 12 Kết nối tri thức
Trong Ví dụ 10, hãy tính các tích vô hướng \(\overrightarrow {AS} .\overrightarrow {BD} \) và \(\overrightarrow {AS} .\overrightarrow {CD} \)
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Sử dụng kiến thức về tích vô hướng của hai vectơ trong không gian để tính: Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Khi đó, \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \cdot \overrightarrow b = 0\)
Lời giải chi tiết:
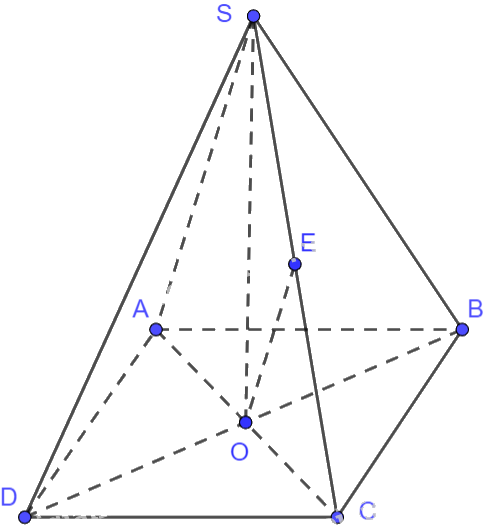
Gọi O là giao điểm của hai đường chéo AC và BD trong hình vuông ABCD. Do đó, O là trung điểm của BD, O là trung điểm của AC.
Tứ giác ABCD là hình vuông cạnh a nên độ dài đường chéo BD là \(a\sqrt 2 \)\( \Rightarrow OB = \frac{{a\sqrt 2 }}{2}\)
Gọi E là trung điểm của SC. Mà O là trung điểm của AC nên OE là đường trung bình của tam giác SAC, do đó, OE//SA, \(OE = \frac{1}{2}SA = \frac{a}{2}\). Suy ra: \(\overrightarrow {AS} = 2\overrightarrow {OE} \)
Vì O là trung điểm của BD nên \(\overrightarrow {BD} = 2\overrightarrow {OB} \)
Vì tam giác SBC có ba cạnh bằng nhau nên tam giác SBC là tam giác đều. Do đó, BE là đường trung tuyến đồng thời là đường cao của tam giác SBC. Do đó, \(EB = \frac{{a\sqrt 3 }}{2}\).
Ta có: \(O{E^2} + O{B^2} = \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} = \frac{{3{a^2}}}{4} = E{B^2}\) nên \(\Delta \)EOB vuông tại O. Do đó, \(\overrightarrow {OE} \bot \overrightarrow {OB} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {BD} = 2\overrightarrow {OE} .\left( { - 2\overrightarrow {OB} } \right) = - 4\overrightarrow {OE} .\overrightarrow {OB} = 0\)
Tứ giác ABCD là hình vuông nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {CD} = \overrightarrow {AS} .\overrightarrow {BA} = - \overrightarrow {AS} .\overrightarrow {AB} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \left( {\overrightarrow {AS} ,\overrightarrow {AB} } \right) = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB}\)
Vì tam giác SAB có ba cạnh bằng nhau nên tam giác SAB đều, suy ra \(\widehat {SAB} = {60^0}\)
Suy ra: \(\overrightarrow {AS} .\overrightarrow {CD} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB} = - a.a.\cos {60^0} = \frac{{ - {a^2}}}{2}\)
Trả lời câu hỏi Luyện tập 11 trang 57SGK Toán 12 Kết nối tri thức
Cho hình lập phương ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 0\).
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Sử dụng kiến thức về tích vô hướng của hai vectơ trong không gian để tính: Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Khi đó, \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a \cdot \overrightarrow b = 0\)
Lời giải chi tiết:
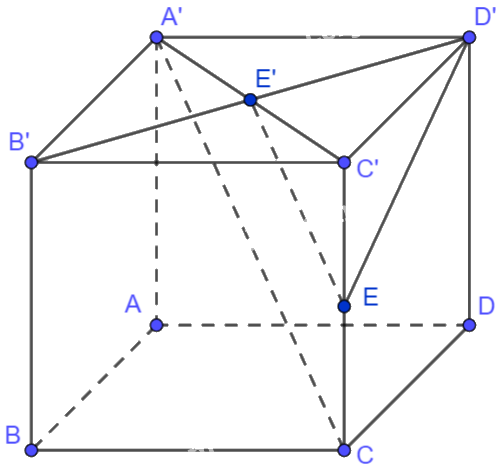
Giả sử cạnh của hình lập phương ABCD.A’B’C’D’ bằng 1. Khi đó, \(A'C' = B'D' = \sqrt 2 \)
Gọi E’ là giao điểm của hai đường chéo A’C’ và B’D’ của hình vuông A’B’C’D’. Khi đó, E’ là trung điểm của A’C’ và B’D’. Suy ra \(\overrightarrow {B'D'} = 2\overrightarrow {E'D'} \) và \(E'D' = \frac{{\sqrt 2 }}{2}\).
Gọi E là trung điểm của CC’. Mà E’ là trung điểm của A’C’ nên EE’ là đường trung bình của tam giác A’C’C. Do đó, \(\overrightarrow {A'C} = 2\overrightarrow {E'E} \) và \(E'E = \frac{1}{2}A'C\)
Áp dụng định lí Pythagore vào \(\Delta \)A’C’C vuông tại C’ có: \(A'C = \sqrt {A'C{'^2} + C'{C^2}} = \sqrt {2 + 1} = \sqrt 3 \)\( \Rightarrow E'E = \frac{{\sqrt 3 }}{2}\)
Áp dụng định lí Pythagore vào \(\Delta \)D’C’E vuông tại C’ có:
\(ED{'^2} = C'D{'^2} + C'{E^2} = 1 + \frac{1}{4} = \frac{5}{4}\)
Vì \(E'D{'^2} + E'{E^2} = \frac{1}{2} + \frac{3}{4} = \frac{5}{4} = ED{'^2}\) nên \(\Delta \)E’D’E vuông tại E’. Do đó, \(\overrightarrow {E'E} \bot \overrightarrow {E'D'} \)
Ta có: \(\overrightarrow {A'C} .\overrightarrow {B'D'} = 2.\overrightarrow {E'E} .2.\overrightarrow {E'D'} \)\( = 0\) (đpcm)
Trả lời câu hỏi Vận dụng 4 trang 57SGK Toán 12 Kết nối tri thức
Như đã biết, nếu có một lực \(\overrightarrow F \) tác động vào một vật tại điểm M và làm cho vật đó di chuyển một quãng đường MN thì công A sinh ra được tính theo công thức \(A = \overrightarrow F .\overrightarrow {MN} \), trong đó lực F có độ lớn tính bằng Newton, quãng đường MN tính bằng mét và công A tính bằng Jun (H.2.28). Do đó, nếu dùng một lực \(\overrightarrow F \) có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao. Kết quả trên có thể được áp dụng như thế nào khi kéo (hoặc đẩy) các vật nặng?
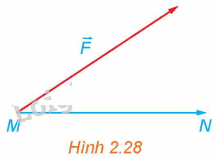
Phương pháp giải:
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để giải thích: Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hương của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết:
Ta có: \(A = \overrightarrow F .\overrightarrow {MN} = \left| {\overrightarrow F } \right|.\left| {\overrightarrow {MN} } \right|.\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right)\)
Vì lực \(\overrightarrow F \) có độ lớn không đổi và vật di chuyển một quãng đường không đổi nên A lớn nhất khi \(\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right)\) lớn nhất. Do đó, \(\cos \left( {\overrightarrow F ,\overrightarrow {MN} } \right) = 1 \Leftrightarrow \left( {\overrightarrow F ,\overrightarrow {MN} } \right) = {0^0}\) . Khi đó, lực tác động cùng hướng với chuyển động của vật. Vậy công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật.
Khi kéo (hoặc đẩy) các vật nặng, ta nên kéo (hoặc đẩy) cùng cùng hướng với chuyển động của vật.
Giải mục 4 trang 54, 55, 56 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 4 trong SGK Toán 12 tập 1 - Kết nối tri thức thường xoay quanh các chủ đề về giới hạn hàm số, đặc biệt là giới hạn tại vô cùng và ứng dụng của giới hạn trong việc tính đạo hàm. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học tiếp theo, đặc biệt là chương trình Giải tích.
Nội dung chính của Mục 4 trang 54, 55, 56
- Giới hạn tại vô cùng: Hiểu rõ khái niệm giới hạn của hàm số khi x tiến tới vô cùng dương hoặc âm.
- Tính chất của giới hạn: Áp dụng các tính chất của giới hạn để đơn giản hóa các bài toán.
- Ứng dụng của giới hạn: Sử dụng giới hạn để tính đạo hàm của hàm số tại một điểm.
- Bài tập thực hành: Giải các bài tập vận dụng kiến thức đã học để củng cố và nâng cao kỹ năng.
Hướng dẫn giải chi tiết các bài tập trong Mục 4
Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 4 trang 54, 55, 56 SGK Toán 12 tập 1 - Kết nối tri thức:
Bài 1: Tính các giới hạn sau
- lim (x -> +∞) (2x + 1) / (x - 2)
- lim (x -> -∞) (x^2 + 3x - 1) / (x + 1)
Giải:
- Bài 1a: lim (x -> +∞) (2x + 1) / (x - 2) = lim (x -> +∞) (2 + 1/x) / (1 - 2/x) = 2/1 = 2
- Bài 1b: lim (x -> -∞) (x^2 + 3x - 1) / (x + 1) = lim (x -> -∞) (x + 2 - 3/(x+1)) = -∞
Bài 2: Cho hàm số f(x) = (x - 1) / (x + 1). Tính f(2), f(-2), lim (x -> ∞) f(x)
Giải:
- f(2) = (2 - 1) / (2 + 1) = 1/3
- f(-2) = (-2 - 1) / (-2 + 1) = -3 / -1 = 3
- lim (x -> ∞) f(x) = lim (x -> ∞) (x - 1) / (x + 1) = lim (x -> ∞) (1 - 1/x) / (1 + 1/x) = 1/1 = 1
Mẹo giải nhanh các bài tập về giới hạn
Để giải nhanh các bài tập về giới hạn, bạn có thể áp dụng một số mẹo sau:
- Chia cả tử và mẫu cho x: Khi tính giới hạn tại vô cùng, hãy chia cả tử và mẫu cho x (hoặc lũy thừa cao nhất của x).
- Sử dụng các công thức giới hạn cơ bản: Nắm vững các công thức giới hạn cơ bản như lim (1/x) = 0 khi x -> ∞.
- Biến đổi đại số: Sử dụng các phép biến đổi đại số để đơn giản hóa biểu thức trước khi tính giới hạn.
Tài liệu tham khảo thêm
Ngoài SGK Toán 12 tập 1 - Kết nối tri thức, bạn có thể tham khảo thêm các tài liệu sau để hiểu sâu hơn về giới hạn:
- Sách bài tập Toán 12
- Các trang web học Toán trực tuyến
- Video bài giảng trên YouTube
Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn khi giải các bài tập về giới hạn trong SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các bạn học tốt!