Giải mục 1 trang 19,20,21 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 19,20,21 SGK Toán 12 tập 2 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu mục 1 trang 19,20,21 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và logic.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
Ứng dụng tích phân để tính diện tích hình phẳng
LT2
Trả lời câu hỏi Luyện tập 2 trang 21 SGK Toán 12 Kết nối tri thức
Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = \sqrt x ,y = x - 2\) và hai đường thẳng \(x = 1,x = 4\).
Phương pháp giải:
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng cần tính là:
\(\int\limits_1^4 {\left| {x - \sqrt x - 2} \right|dx} = - \int\limits_1^4 {\left( {x - \sqrt x - 2} \right)dx} = - \left( {\frac{{{x^2}}}{2} - \frac{{2x\sqrt x }}{3} - 2x} \right)\left| \begin{array}{l}4\\1\end{array} \right.\)
\( = - \left( {\frac{{{4^2}}}{2} - \frac{{2.4\sqrt 4 }}{3} - 2.4 - \frac{1}{2} + \frac{{2.1.\sqrt 1 }}{3} + 2.1} \right) = \frac{{19}}{6}\)
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 19 SGK Toán 12 Kết nối tri thức
Xét hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right) = x + 1\), trục hoành và hai đường thẳng \(x = - 2,x = 1\) (H.4.12).
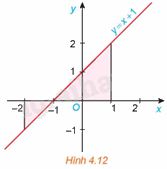
a) Tính diện tích S của hình phẳng này.
b) Tính \(\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} \) và so sánh với S.
Phương pháp giải:
Sử dụng kiến thức về tính chất của tích phân để tính: Cho f(x), g(x) là các hàm số liên tục trên đoạn [a; b]. Khi đó, ta có: \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \) \(\left( {a < c < b} \right)\).
Lời giải chi tiết:
a) Đặt tên các điểm như hình vẽ. Khi đó, \(AD = 1,DE = 1,AC = 2,CB = 2\)

Diện tích S của hình phẳng là:
\(S = {S_{\Delta EAD}} + {S_{\Delta ABC}} = \frac{1}{2}AD.DE + \frac{1}{2}AC.BC = \frac{1}{2}.1.1 + \frac{1}{2}.2.2 = \frac{1}{2} + 2 = \frac{5}{2}\)
b) \(\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^1 {\left| {x + 1} \right|dx} = \int\limits_{ - 2}^{ - 1} {\left| {x + 1} \right|dx} + \int\limits_{ - 1}^1 {\left| {x + 1} \right|dx = - \int\limits_{ - 2}^{ - 1} {\left( {x + 1} \right)dx} + \int\limits_{ - 1}^1 {\left( {x + 1} \right)dx} } \)
\( = - \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l} - 1\\ - 2\end{array} \right. + \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l}1\\ - 1\end{array} \right. = \left( {\frac{1}{2} + 1 - \frac{1}{2} + 1} \right) - \left( {\frac{{{1^2}}}{2} - 1 - \frac{{{{\left( { - 2} \right)}^2}}}{2} + 2} \right) = 2 + \frac{1}{2} = \frac{5}{2}\)
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Kết nối tri thức
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(f\left( x \right) = - {x^2} + 4x,\) \(g\left( x \right) = x\) và hai đường thẳng \(x = 1,x = 3\) (H.4.16)
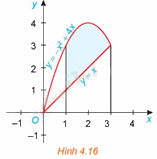
a) Giả sử \({S_1}\) là diện tích hình phẳng giới hạn bởi parabol \(y = - {x^2} + 4x\), trục hoành và hai đường thẳng \(x = 1,x = 3\); \({S_2}\) là diện tích hình phẳng giới hạn bởi đường thẳng \(y = x\), trục hoành và hai đường thẳng \(x = 1,x = 3\). Tính \({S_1}\), \({S_2}\) và từ đó suy ra S.
b) Tính \(\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) và so sánh với S.
Phương pháp giải:
Sử dụng kiến thức về ứng dụng tích phân để tính diện tích hình phẳng để tính: Diện tích S của hàm số f(x) liên tục, trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
a) Diện tích hình phẳng giới hạn bởi parabol \(y = - {x^2} + 4x\), trục hoành và hai đường thẳng \(x = 1,x = 3\) là:
\({S_1} = \int\limits_1^3 {\left| { - {x^2} + 4x} \right|dx} = \int\limits_1^3 {\left( { - {x^2} + 4x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + 2{x^2}} \right)\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{ - {3^3}}}{3} + {2.3^2} + \frac{1}{3} - {2.1^2} = \frac{{22}}{3}\)
Diện tích hình phẳng giới hạn bởi parabol \(y = x\), trục hoành và hai đường thẳng \(x = 1,x = 3\) là: \({S_2} = \int\limits_1^3 {\left| x \right|dx} = \int\limits_1^3 {xdx} = \frac{{{x^2}}}{2}\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{{3^2}}}{2} - \frac{1}{2} = 4\)
Do đó, \(S = {S_1} - {S_2} = \frac{{22}}{3} - 4 = \frac{{10}}{3}\)
b) \(\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_1^3 {\left| { - {x^2} + 3x} \right|dx} = \int\limits_1^3 {\left( { - {x^2} + 3x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + \frac{{3{x^2}}}{2}} \right)\left| \begin{array}{l}3\\1\end{array} \right.\)
\( = \frac{{ - {3^3}}}{3} + \frac{{{{3.3}^2}}}{2} + \frac{1}{3} - \frac{3}{2} = \frac{{10}}{3}\)
Do đó, \(S = \int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
LT1
Trả lời câu hỏi Luyện tập 1 trang 20 SGK Toán 12 Kết nối tri thức
Tính diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} - 4\), trục hoành và hai đường thẳng \(x = 0,x = 3\) (H.4.15).
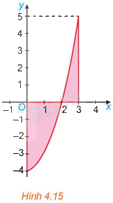
Phương pháp giải:
Sử dụng kiến thức về ứng dụng tích phân để tính diện tích hình phẳng để tính: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f(x) liên tục, trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng cần tính là:
\(S = \int\limits_0^3 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx} + \int\limits_2^3 {\left| {{x^2} - 4} \right|dx} = - \int\limits_0^2 {\left( {{x^2} - 4} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 4} \right)dx} \)
\( = - \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}2\\0\end{array} \right. + \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}3\\2\end{array} \right. = - \left( {\frac{{{2^3}}}{3} - 4.2} \right) + \left( {\frac{{{3^3}}}{3} - 4.3 - \frac{{{2^3}}}{3} + 4.2} \right) = \frac{{16}}{3} + \frac{7}{3} = \frac{{23}}{3}\)
VD1
Trả lời câu hỏi Vận dụng 1 trang 22 SGK Toán 12 Kết nối tri thức
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{x_o};{p_o}} \right)\) của đồ thị hàm cầu \(p = D\left( x \right)\) và đồ thị hàm cung \(p = S\left( x \right)\) được gọi là điểm cân bằng.
Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như trong Hình 4.19.
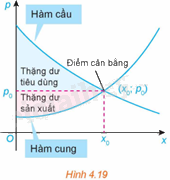
(Theo R. Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009)
Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:
Hàm cầu: \(p = - 0,36x + 9\) và hàm cung: \(p = 0,14x + 2\), trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.
Phương pháp giải:
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Gọi điểm M là giao điểm của hàm cầu \(p = - 0,36x + 9\) và hàm cung \(p = 0,14x + 2\)
Khi đó, phương trình hoành độ giao điểm của hàm cầu và hàm cung là:
\( - 0,36x + 9 = 0,14x + 2\), suy ra \(x = 14\) nên \(p = - 0,36.14 + 9 = \frac{{99}}{{25}}\). Do đó, \(M\left( {14;\frac{{99}}{{25}}} \right)\)
Đồ thị hàm số \(p = - 0,36x + 9\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm N(0 ;9)
Đồ thị hàm số \(p = 0,14x + 2\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm P(0; 2)

Diện tích hình giới hạn bởi đồ thị hàm số \(p = - 0,36x + 9\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là: \({S_1} = \int\limits_0^{14} {\left| { - 0,36x + 9} \right|dx} = \int\limits_0^{14} {\left( { - 0,36x + 9} \right)dx} = \left( { - 0,18{x^2} + 9x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)
\( = - 0,{18.14^2} + 9.14 = 90,72\)
Diện tích hình giới hạn bởi đồ thị hàm số \(p = 0,14x + 2\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là:
\({S_2} = \int\limits_0^{14} {\left| {0,14x + 2} \right|dx} = \int\limits_0^{14} {\left( {0,14x + 2} \right)dx} = \left( {0,07{x^2} + 2x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)\( = 0,{07.14^2} + 2.14 = 41,72\)
Thặng dư tiêu dùng cho sản phẩm này là: \({S_1} - OQ.QM = 90,72 - 14.\frac{{99}}{{25}} = 35,28\)
Thặng dư sản xuất cho sản phẩm này là: \(OQ.QM - {S_2} = 14.\frac{{99}}{{25}} - 41,72 = 13,72\)
- HĐ1
- LT1
- HĐ2
- LT2
- VD1
Trả lời câu hỏi Hoạt động 1 trang 19 SGK Toán 12 Kết nối tri thức
Xét hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right) = x + 1\), trục hoành và hai đường thẳng \(x = - 2,x = 1\) (H.4.12).
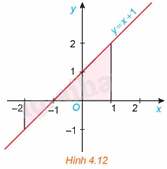
a) Tính diện tích S của hình phẳng này.
b) Tính \(\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} \) và so sánh với S.
Phương pháp giải:
Sử dụng kiến thức về tính chất của tích phân để tính: Cho f(x), g(x) là các hàm số liên tục trên đoạn [a; b]. Khi đó, ta có: \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \) \(\left( {a < c < b} \right)\).
Lời giải chi tiết:
a) Đặt tên các điểm như hình vẽ. Khi đó, \(AD = 1,DE = 1,AC = 2,CB = 2\)
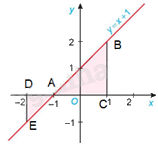
Diện tích S của hình phẳng là:
\(S = {S_{\Delta EAD}} + {S_{\Delta ABC}} = \frac{1}{2}AD.DE + \frac{1}{2}AC.BC = \frac{1}{2}.1.1 + \frac{1}{2}.2.2 = \frac{1}{2} + 2 = \frac{5}{2}\)
b) \(\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^1 {\left| {x + 1} \right|dx} = \int\limits_{ - 2}^{ - 1} {\left| {x + 1} \right|dx} + \int\limits_{ - 1}^1 {\left| {x + 1} \right|dx = - \int\limits_{ - 2}^{ - 1} {\left( {x + 1} \right)dx} + \int\limits_{ - 1}^1 {\left( {x + 1} \right)dx} } \)
\( = - \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l} - 1\\ - 2\end{array} \right. + \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l}1\\ - 1\end{array} \right. = \left( {\frac{1}{2} + 1 - \frac{1}{2} + 1} \right) - \left( {\frac{{{1^2}}}{2} - 1 - \frac{{{{\left( { - 2} \right)}^2}}}{2} + 2} \right) = 2 + \frac{1}{2} = \frac{5}{2}\)
Trả lời câu hỏi Luyện tập 1 trang 20 SGK Toán 12 Kết nối tri thức
Tính diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} - 4\), trục hoành và hai đường thẳng \(x = 0,x = 3\) (H.4.15).
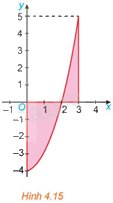
Phương pháp giải:
Sử dụng kiến thức về ứng dụng tích phân để tính diện tích hình phẳng để tính: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f(x) liên tục, trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng cần tính là:
\(S = \int\limits_0^3 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx} + \int\limits_2^3 {\left| {{x^2} - 4} \right|dx} = - \int\limits_0^2 {\left( {{x^2} - 4} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 4} \right)dx} \)
\( = - \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}2\\0\end{array} \right. + \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}3\\2\end{array} \right. = - \left( {\frac{{{2^3}}}{3} - 4.2} \right) + \left( {\frac{{{3^3}}}{3} - 4.3 - \frac{{{2^3}}}{3} + 4.2} \right) = \frac{{16}}{3} + \frac{7}{3} = \frac{{23}}{3}\)
Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Kết nối tri thức
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(f\left( x \right) = - {x^2} + 4x,\) \(g\left( x \right) = x\) và hai đường thẳng \(x = 1,x = 3\) (H.4.16)
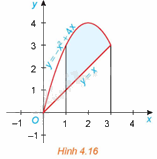
a) Giả sử \({S_1}\) là diện tích hình phẳng giới hạn bởi parabol \(y = - {x^2} + 4x\), trục hoành và hai đường thẳng \(x = 1,x = 3\); \({S_2}\) là diện tích hình phẳng giới hạn bởi đường thẳng \(y = x\), trục hoành và hai đường thẳng \(x = 1,x = 3\). Tính \({S_1}\), \({S_2}\) và từ đó suy ra S.
b) Tính \(\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) và so sánh với S.
Phương pháp giải:
Sử dụng kiến thức về ứng dụng tích phân để tính diện tích hình phẳng để tính: Diện tích S của hàm số f(x) liên tục, trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
a) Diện tích hình phẳng giới hạn bởi parabol \(y = - {x^2} + 4x\), trục hoành và hai đường thẳng \(x = 1,x = 3\) là:
\({S_1} = \int\limits_1^3 {\left| { - {x^2} + 4x} \right|dx} = \int\limits_1^3 {\left( { - {x^2} + 4x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + 2{x^2}} \right)\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{ - {3^3}}}{3} + {2.3^2} + \frac{1}{3} - {2.1^2} = \frac{{22}}{3}\)
Diện tích hình phẳng giới hạn bởi parabol \(y = x\), trục hoành và hai đường thẳng \(x = 1,x = 3\) là: \({S_2} = \int\limits_1^3 {\left| x \right|dx} = \int\limits_1^3 {xdx} = \frac{{{x^2}}}{2}\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{{3^2}}}{2} - \frac{1}{2} = 4\)
Do đó, \(S = {S_1} - {S_2} = \frac{{22}}{3} - 4 = \frac{{10}}{3}\)
b) \(\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_1^3 {\left| { - {x^2} + 3x} \right|dx} = \int\limits_1^3 {\left( { - {x^2} + 3x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + \frac{{3{x^2}}}{2}} \right)\left| \begin{array}{l}3\\1\end{array} \right.\)
\( = \frac{{ - {3^3}}}{3} + \frac{{{{3.3}^2}}}{2} + \frac{1}{3} - \frac{3}{2} = \frac{{10}}{3}\)
Do đó, \(S = \int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
Trả lời câu hỏi Luyện tập 2 trang 21 SGK Toán 12 Kết nối tri thức
Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = \sqrt x ,y = x - 2\) và hai đường thẳng \(x = 1,x = 4\).
Phương pháp giải:
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng cần tính là:
\(\int\limits_1^4 {\left| {x - \sqrt x - 2} \right|dx} = - \int\limits_1^4 {\left( {x - \sqrt x - 2} \right)dx} = - \left( {\frac{{{x^2}}}{2} - \frac{{2x\sqrt x }}{3} - 2x} \right)\left| \begin{array}{l}4\\1\end{array} \right.\)
\( = - \left( {\frac{{{4^2}}}{2} - \frac{{2.4\sqrt 4 }}{3} - 2.4 - \frac{1}{2} + \frac{{2.1.\sqrt 1 }}{3} + 2.1} \right) = \frac{{19}}{6}\)
Trả lời câu hỏi Vận dụng 1 trang 22 SGK Toán 12 Kết nối tri thức
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{x_o};{p_o}} \right)\) của đồ thị hàm cầu \(p = D\left( x \right)\) và đồ thị hàm cung \(p = S\left( x \right)\) được gọi là điểm cân bằng.
Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như trong Hình 4.19.
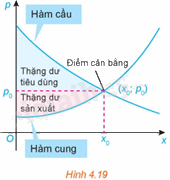
(Theo R. Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009)
Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:
Hàm cầu: \(p = - 0,36x + 9\) và hàm cung: \(p = 0,14x + 2\), trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.
Phương pháp giải:
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Gọi điểm M là giao điểm của hàm cầu \(p = - 0,36x + 9\) và hàm cung \(p = 0,14x + 2\)
Khi đó, phương trình hoành độ giao điểm của hàm cầu và hàm cung là:
\( - 0,36x + 9 = 0,14x + 2\), suy ra \(x = 14\) nên \(p = - 0,36.14 + 9 = \frac{{99}}{{25}}\). Do đó, \(M\left( {14;\frac{{99}}{{25}}} \right)\)
Đồ thị hàm số \(p = - 0,36x + 9\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm N(0 ;9)
Đồ thị hàm số \(p = 0,14x + 2\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm P(0; 2)
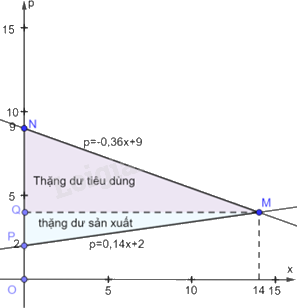
Diện tích hình giới hạn bởi đồ thị hàm số \(p = - 0,36x + 9\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là: \({S_1} = \int\limits_0^{14} {\left| { - 0,36x + 9} \right|dx} = \int\limits_0^{14} {\left( { - 0,36x + 9} \right)dx} = \left( { - 0,18{x^2} + 9x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)
\( = - 0,{18.14^2} + 9.14 = 90,72\)
Diện tích hình giới hạn bởi đồ thị hàm số \(p = 0,14x + 2\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là:
\({S_2} = \int\limits_0^{14} {\left| {0,14x + 2} \right|dx} = \int\limits_0^{14} {\left( {0,14x + 2} \right)dx} = \left( {0,07{x^2} + 2x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)\( = 0,{07.14^2} + 2.14 = 41,72\)
Thặng dư tiêu dùng cho sản phẩm này là: \({S_1} - OQ.QM = 90,72 - 14.\frac{{99}}{{25}} = 35,28\)
Thặng dư sản xuất cho sản phẩm này là: \(OQ.QM - {S_2} = 14.\frac{{99}}{{25}} - 41,72 = 13,72\)
Giải mục 1 trang 19,20,21 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 trang 19,20,21 SGK Toán 12 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, nền tảng cho việc giải quyết các bài toán phức tạp hơn trong các chương tiếp theo và kỳ thi tốt nghiệp THPT. Để giải tốt các bài tập trong mục này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
- Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và trên một khoảng.
- Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số thường gặp: Biết đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
- Ứng dụng của đạo hàm: Hiểu cách sử dụng đạo hàm để xét tính đơn điệu, cực trị của hàm số.
Nội dung chi tiết Giải mục 1 trang 19,20,21
Mục 1 bao gồm các bài tập trắc nghiệm và tự luận, yêu cầu học sinh vận dụng các kiến thức về đạo hàm để giải quyết các vấn đề cụ thể. Dưới đây là giải chi tiết từng bài tập:
Bài 1: Trắc nghiệm
Các bài tập trắc nghiệm trong mục này thường tập trung vào việc kiểm tra khả năng hiểu và vận dụng các quy tắc tính đạo hàm. Để giải tốt các bài tập này, học sinh cần:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Sử dụng các quy tắc tính đạo hàm một cách chính xác.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
Bài 2: Tự luận
Các bài tập tự luận yêu cầu học sinh trình bày chi tiết các bước giải. Để đạt điểm cao, học sinh cần:
- Viết rõ ràng, mạch lạc và dễ hiểu.
- Sử dụng các ký hiệu toán học một cách chính xác.
- Giải thích rõ ràng các bước giải.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
Ví dụ minh họa
Bài tập: Tính đạo hàm của hàm số f(x) = x2 + 2x - 1.
Giải:
f'(x) = 2x + 2
Mẹo giải nhanh
Để giải nhanh các bài tập về đạo hàm, học sinh có thể sử dụng các mẹo sau:
- Nắm vững bảng đạo hàm của các hàm số thường gặp.
- Sử dụng các quy tắc tính đạo hàm một cách linh hoạt.
- Luyện tập thường xuyên để rèn luyện kỹ năng.
Tài liệu tham khảo
Ngoài SGK Toán 12 tập 2 - Kết nối tri thức, học sinh có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 12 tập 2 - Kết nối tri thức.
- Các trang web học Toán trực tuyến.
- Các video bài giảng về đạo hàm.
Kết luận
Giải mục 1 trang 19,20,21 SGK Toán 12 tập 2 - Kết nối tri thức là một bước quan trọng trong quá trình ôn tập và chuẩn bị cho kỳ thi tốt nghiệp THPT. Hy vọng với lời giải chi tiết và các mẹo giải nhanh mà Tusach.vn cung cấp, các em học sinh sẽ tự tin hơn khi đối mặt với các bài tập về đạo hàm.