Giải bài tập 1.13 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 1.13 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.13 trang 19 SGK Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Đề bài
Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm giá trị lớn nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f'\left( x \right) = 0\).
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\):
1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f'\left( x \right) = 0\) hoặc không tồn tại.
2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.
Ta có: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\)
Lời giải chi tiết
Gọi chiều dài của hình chữ nhật là x (cm, \(0 < x < 12\))
Chiều rộng của hình chữ nhật là \(12 - x\left( {cm} \right)\)
Diện tích của hình chữ nhật là: \(x\left( {12 - x} \right) = - {x^2} + 12x\;\left( {c{m^2}} \right)\)
Đặt \(S\left( x \right) = - {x^2} + 12x,x \in \left( {0;12} \right)\)
\(S'\left( x \right) = - 2x + 12,S'\left( x \right) = 0 \Leftrightarrow x = 6\left( {tm} \right)\)
Bảng biến thiên:
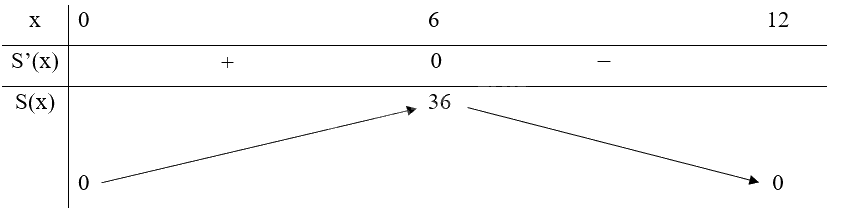
Do đó, trong các hình có cùng chu vi thì hình chữ nhật có diện tích lớn nhất là \(36c{m^2}\).
Giải Bài Tập 1.13 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 1.13 trang 19 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu chúng ta vận dụng kiến thức về giới hạn của hàm số để xét tính liên tục của hàm số tại một điểm. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững định nghĩa về giới hạn và các tính chất của giới hạn.
Nội Dung Bài Tập 1.13
Bài tập 1.13 thường có dạng như sau: Cho hàm số f(x) được xác định bởi:
- f(x) = ... (biểu thức hàm số) khi x ≠ x0
- f(x0) = ... (giá trị của hàm số tại x0)
Yêu cầu: Xét tính liên tục của hàm số f(x) tại điểm x0.
Phương Pháp Giải Bài Tập 1.13
- Tính giới hạn của hàm số f(x) khi x tiến tới x0: Sử dụng các quy tắc tính giới hạn, các công thức giới hạn đặc biệt và các phương pháp như nhân liên hợp, chia đa thức để tính limx→x0 f(x).
- Tính giá trị của hàm số f(x) tại x0: Giá trị này thường được cho sẵn trong đề bài.
- So sánh giới hạn và giá trị của hàm số:
- Nếu limx→x0 f(x) = f(x0) thì hàm số f(x) liên tục tại x0.
- Nếu limx→x0 f(x) ≠ f(x0) thì hàm số f(x) không liên tục tại x0.
Ví Dụ Minh Họa
Ví dụ: Xét hàm số f(x) = (x2 - 1) / (x - 1) khi x ≠ 1 và f(1) = 2. Hàm số f(x) có liên tục tại x = 1 hay không?
Giải:
- Tính giới hạn: limx→1 f(x) = limx→1 (x2 - 1) / (x - 1) = limx→1 (x + 1) = 2
- Giá trị hàm số: f(1) = 2
- So sánh: limx→1 f(x) = f(1) = 2
Vậy hàm số f(x) liên tục tại x = 1.
Lưu Ý Quan Trọng
- Luôn kiểm tra xem hàm số có xác định tại điểm x0 hay không.
- Chú ý đến các dạng giới hạn vô định và sử dụng các phương pháp phù hợp để khử dạng vô định.
- Nắm vững các định nghĩa và tính chất của giới hạn để áp dụng một cách chính xác.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK và sách bài tập Toán 12 tập 1 Kết nối tri thức. Ngoài ra, các em có thể tham khảo thêm các tài liệu ôn tập và luyện thi trên tusach.vn.
Kết Luận
Việc giải bài tập 1.13 trang 19 SGK Toán 12 tập 1 Kết nối tri thức đòi hỏi sự hiểu biết vững chắc về giới hạn và tính liên tục của hàm số. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.