Đề bài
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Cho các hàm số đa thức sau:
(1) \(y = 3{x^2} + \sqrt 3 x + 1\); (2) \(y = {x^3} - 6{x^2} + 9\), (3) \(y = {x^4} - 4{x^2} + 3\).
a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên.
b) Tìm tất cả các điểm cực trị của các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Phương pháp giải - Xem chi tiết
a, b) Sử dụng kiến thức về các cú pháp lệnh trong GeoGebra để thực hiện:
c) Sử dụng kiến thức về vẽ đồ thị của hàm đa thức để vẽ đồ thị hàm số: Nhập hàm số vào ô lệnh, màn hình sẽ hiển thị đồ thị hàm số cần vẽ.
Lời giải chi tiết
a) Hàm số \(y = 3{x^2} + \sqrt 3 x + 1\)
Để tính đạo hàm cấp 1 ta nhập DaoHam (\(3{x^2} + \sqrt 3 x + 1\))
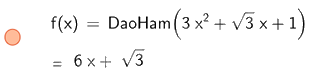
Do đó, đạo hàm cấp 1 của hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) là \(6x + \sqrt 3 \)
Để tính đạo hàm cấp 2 ta nhập DaoHam (\(3{x^2} + \sqrt 3 x + 1\), 2)
Do đó, đạo hàm cấp 2 của hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) là \(6\)
Hàm số \(y = {x^3} - 6{x^2} + 9\)
Để tính đạo hàm cấp 1 ta nhập DaoHam (\({x^3} - 6{x^2} + 9\))
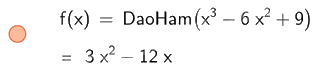
Do đó, đạo hàm cấp 1 của hàm số \(y = {x^3} - 6{x^2} + 9\) là \(3{x^2} - 12x\)
Để tính đạo hàm cấp 2 ta nhập DaoHam (, 2)
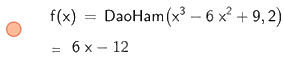
Do đó, đạo hàm cấp 2 của hàm số \(y = {x^3} - 6{x^2} + 9\) là \(6x - 12\)
Hàm số \(y = {x^4} - 4{x^2} + 3\)
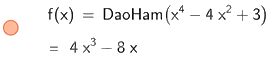
Để tính đạo hàm cấp 1 ta nhập DaoHam (\({x^4} - 4{x^2} + 3\))
Do đó, đạo hàm cấp 1 của hàm số \(y = {x^4} - 4{x^2} + 3\) là \(4{x^3} - 8x\)
Để tính đạo hàm cấp 2 ta nhập DaoHam (\({x^4} - 4{x^2} + 3\), 2)
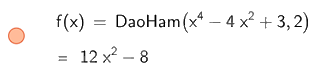
Do đó, đạo hàm cấp 2 của hàm số \(y = {x^4} - 4{x^2} + 3\) là \(12{x^2} - 8\)
b) Hàm số \(y = 3{x^2} + \sqrt 3 x + 1\)
Để tìm cực trị ta nhập lệnh, kết quả hiện thị ngay bên dưới:
Do đó, hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) có điểm cực trị là \(\left( {\frac{{ - \sqrt 3 }}{6};0,75} \right)\)
Hàm số \(y = {x^3} - 6{x^2} + 9\)
Để tìm cực trị ta nhập lệnh, kết quả hiện thị ngay bên dưới:
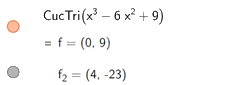
Do đó, hàm số \(y = {x^3} - 6{x^2} + 9\) có các điểm cực trị là \(\left( {0;9} \right);\left( {4; - 23} \right)\)
Hàm số \(y = {x^4} - 4{x^2} + 3\)
Để tìm cực trị ta nhập lệnh, kết quả hiện thị ngay bên dưới:
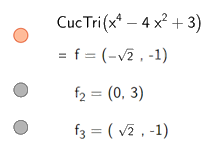
Do đó, hàm số \(y = {x^4} - 4{x^2} + 3\) có các điểm cực trị là \(\left( { - \sqrt 2 ; - 1} \right);\left( {0;3} \right);\left( {\sqrt 2 ; - 1} \right)\)
c) Đồ thị hàm số \(y = 3{x^2} + \sqrt 3 x + 1\): Ta nhập hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ:
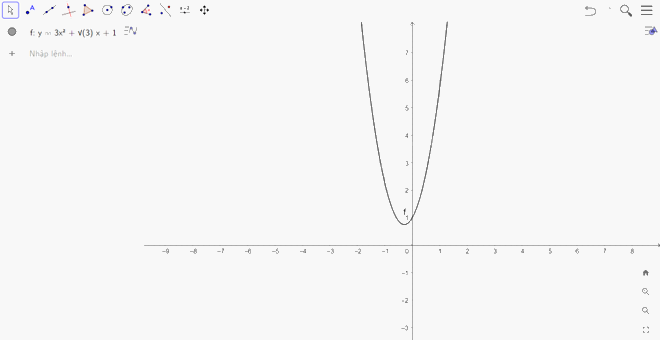
Đồ thị hàm số \(y = {x^3} - 6{x^2} + 9\): Ta nhập hàm số \(y = {x^3} - 6{x^2} + 9\) vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ:
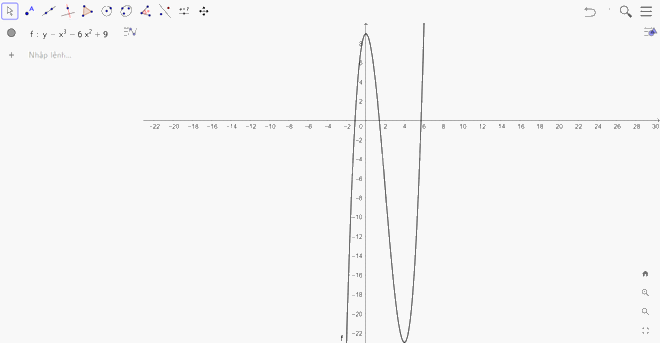
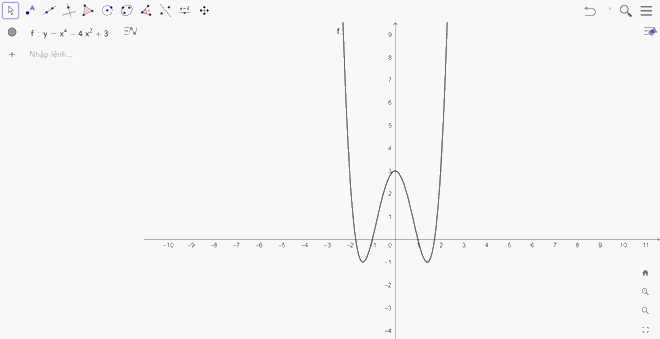
Đồ thị hàm số \(y = {x^4} - 4{x^2} + 3\): Ta nhập hàm số \(y = {x^4} - 4{x^2} + 3\) vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ:
