Giải mục 2 trang 21, 22 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 21, 22 SGK Toán 12 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 21, 22 SGK Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin làm bài tập.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Đường tiệm cận đứng
LT2
Trả lời câu hỏi Luyện tập 2 trang 22 SGK Toán 12 Kết nối tri thức
Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x - 4}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{1}{x}}}{{1 - \frac{4}{x}}} = 2;\mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 1}}{{x - 4}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 + \frac{1}{x}}}{{1 - \frac{4}{x}}} = 2\) nên tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\) là \(y = 2\).
Lại có: \(\mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ + }} \frac{{2x + 1}}{{x - 4}} = + \infty ;\mathop {\lim }\limits_{x \to {4^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \frac{{2x + 1}}{{x - 4}} = - \infty \) nên tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\) đường thẳng \(x = 4\).
VD2
Trả lời câu hỏi Vận dụng 2 trang 22 SGK Toán 12 Kết nối tri thức
Để loại bỏ p% một loài tảo độc khỏi hồ nước, người ta ước tính chi phí bỏ ra là \(C\left( p \right) = \frac{{45p}}{{100 - p}}\) (triệu đồng), với \(0 \le p < 100\). Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa của đường tiệm cận này.
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{p \to {{100}^ - }} C\left( p \right) = \mathop {\lim }\limits_{p \to {{100}^ - }} \frac{{45p}}{{100 - p}} = + \infty \) nên tiệm cận đứng của đồ thị hàm số C(p) là \(p = 100\).
Ý nghĩa của đường tiệm cận là: Không thể loại bỏ hết loài tảo độc ra khỏi hồ nước dù chi phí là bao nhiêu.
- HĐ2
- LT2
- VD2
Trả lời câu hỏi Hoạt động 2 trang 21 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \frac{x}{{x - 1}}\) có đồ thị (C). Với \(x > 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(x = 1\) (H.1.22).
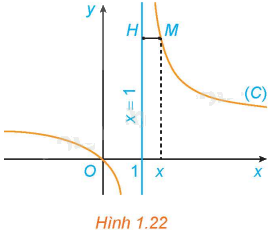
a) Tính khoảng cách MH.
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?
Phương pháp giải:
Sử dụng kiến thức về đọc đồ thị hàm số để đưa ra nhận xét.
Lời giải chi tiết:
a) Ta có: \(M\left( {x;\frac{x}{{x - 1}}} \right);H\left( {1;\frac{x}{{x - 1}}} \right)\)
Do đó, \(MH = \sqrt {{{\left( {1 - x} \right)}^2} + {{\left( {\frac{x}{{x - 1}} - \frac{x}{{x - 1}}} \right)}^2}} = x - 1\) (do \(x > 1\))
b) Khi khoảng cách MH dần đến 0 thì tung độ của điểm M dần ra xa vô tận về phía trên (tung độ điểm M tiến ra \( + \infty \)).
Trả lời câu hỏi Luyện tập 2 trang 22 SGK Toán 12 Kết nối tri thức
Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x - 4}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{1}{x}}}{{1 - \frac{4}{x}}} = 2;\mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 1}}{{x - 4}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 + \frac{1}{x}}}{{1 - \frac{4}{x}}} = 2\) nên tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\) là \(y = 2\).
Lại có: \(\mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ + }} \frac{{2x + 1}}{{x - 4}} = + \infty ;\mathop {\lim }\limits_{x \to {4^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \frac{{2x + 1}}{{x - 4}} = - \infty \) nên tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\) đường thẳng \(x = 4\).
Trả lời câu hỏi Vận dụng 2 trang 22 SGK Toán 12 Kết nối tri thức
Để loại bỏ p% một loài tảo độc khỏi hồ nước, người ta ước tính chi phí bỏ ra là \(C\left( p \right) = \frac{{45p}}{{100 - p}}\) (triệu đồng), với \(0 \le p < 100\). Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa của đường tiệm cận này.
Phương pháp giải:
Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{p \to {{100}^ - }} C\left( p \right) = \mathop {\lim }\limits_{p \to {{100}^ - }} \frac{{45p}}{{100 - p}} = + \infty \) nên tiệm cận đứng của đồ thị hàm số C(p) là \(p = 100\).
Ý nghĩa của đường tiệm cận là: Không thể loại bỏ hết loài tảo độc ra khỏi hồ nước dù chi phí là bao nhiêu.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 21 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \frac{x}{{x - 1}}\) có đồ thị (C). Với \(x > 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(x = 1\) (H.1.22).
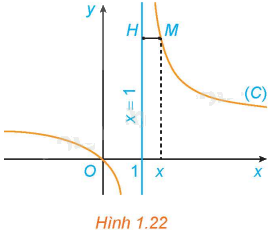
a) Tính khoảng cách MH.
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?
Phương pháp giải:
Sử dụng kiến thức về đọc đồ thị hàm số để đưa ra nhận xét.
Lời giải chi tiết:
a) Ta có: \(M\left( {x;\frac{x}{{x - 1}}} \right);H\left( {1;\frac{x}{{x - 1}}} \right)\)
Do đó, \(MH = \sqrt {{{\left( {1 - x} \right)}^2} + {{\left( {\frac{x}{{x - 1}} - \frac{x}{{x - 1}}} \right)}^2}} = x - 1\) (do \(x > 1\))
b) Khi khoảng cách MH dần đến 0 thì tung độ của điểm M dần ra xa vô tận về phía trên (tung độ điểm M tiến ra \( + \infty \)).
Giải mục 2 trang 21, 22 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 12 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc hiểu các khái niệm nâng cao hơn như đạo hàm và tích phân. Việc nắm vững kiến thức về giới hạn hàm số không chỉ giúp các em giải quyết các bài tập trong SGK mà còn là bước đệm quan trọng cho các kỳ thi quan trọng như THPT Quốc gia.
Nội dung chính của Mục 2
- Khái niệm giới hạn của hàm số tại một điểm: Hiểu rõ định nghĩa, ý nghĩa và các điều kiện để một hàm số có giới hạn tại một điểm.
- Tính chất của giới hạn hàm số: Nắm vững các tính chất cơ bản của giới hạn, bao gồm giới hạn của tổng, hiệu, tích, thương và lũy thừa.
- Các dạng giới hạn thường gặp: Làm quen với các dạng giới hạn đặc biệt như giới hạn vô cùng, giới hạn tại vô cùng và giới hạn của các hàm số lượng giác.
- Ứng dụng của giới hạn hàm số: Sử dụng giới hạn để giải quyết các bài toán về sự liên tục của hàm số và các bài toán thực tế.
Giải chi tiết bài tập trang 21, 22 SGK Toán 12 tập 1 - Kết nối tri thức
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 21, 22 SGK Toán 12 tập 1 Kết nối tri thức:
Bài 1: Tính các giới hạn sau
- lim (x→2) (x^2 + 3x - 1)
- lim (x→-1) (2x^3 - 5x + 1)
- lim (x→0) (x^2 + 1) / (x - 1)
Lời giải:
- a) lim (x→2) (x^2 + 3x - 1) = 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9
- b) lim (x→-1) (2x^3 - 5x + 1) = 2*(-1)^3 - 5*(-1) + 1 = -2 + 5 + 1 = 4
- c) lim (x→0) (x^2 + 1) / (x - 1) = (0^2 + 1) / (0 - 1) = 1 / -1 = -1
Bài 2: Cho hàm số f(x) = (x^2 - 1) / (x - 1). Tính lim (x→1) f(x)
Lời giải:
Ta có f(x) = (x^2 - 1) / (x - 1) = (x - 1)(x + 1) / (x - 1). Với x ≠ 1, ta có f(x) = x + 1. Do đó, lim (x→1) f(x) = lim (x→1) (x + 1) = 1 + 1 = 2.
Bài 3: ... (Tiếp tục giải các bài tập còn lại)
Mẹo giải bài tập về giới hạn hàm số
- Phân tích và rút gọn biểu thức: Trước khi tính giới hạn, hãy cố gắng phân tích và rút gọn biểu thức để đơn giản hóa bài toán.
- Sử dụng các tính chất của giới hạn: Áp dụng các tính chất của giới hạn để tách, nhóm và biến đổi biểu thức.
- Chú ý đến các dạng giới hạn đặc biệt: Nhận biết và sử dụng các công thức giới hạn đặc biệt để giải quyết nhanh chóng các bài toán.
- Kiểm tra lại kết quả: Sau khi tính giới hạn, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Kết luận
Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh đã nắm vững kiến thức về giới hạn hàm số và tự tin giải quyết các bài tập trong SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tập tốt!
Đừng quên truy cập tusach.vn để xem thêm nhiều tài liệu học tập hữu ích khác.