Giải bài tập 1.14 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 1.14 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.14 trang 19 SGK Toán 12 tập 1 Kết nối tri thức. Bài tập này thuộc chương trình học về giới hạn của hàm số, một trong những kiến thức nền tảng quan trọng của môn Toán 12.
tusach.vn sẽ cung cấp lời giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
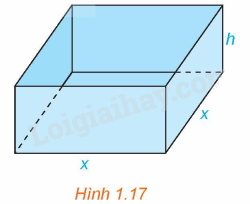
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng (108c{m^2}) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Đề bài
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng \(108c{m^2}\) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm giá trị lớn nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f'\left( x \right) = 0\).
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\):
1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f'\left( x \right) = 0\) hoặc không tồn tại.
2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
\(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\)
Lời giải chi tiết
Hình hộp trên có độ dài cạnh đáy là x (cm, \(0 < x < \sqrt {108} \)) và chiều cao là h (cm, \(h > 0\)).
Diện tích bề mặt của hình hộp là \(108c{m^2}\) nên \({x^2} + 4xh = 108 \Rightarrow h = \frac{{108 - {x^2}}}{{4x}}\left( {cm} \right)\).
Thể tích của hình hộp là: \(V = {x^2}.h = {x^2}.\frac{{108 - {x^2}}}{{4x}} = \frac{{108x - {x^3}}}{4}\left( {c{m^3}} \right)\).
Ta có: \(V' = \frac{{ - 3{x^2} + 108}}{4},V' = 0 \Leftrightarrow x = 6\) (do \(x > 0\)).
Bảng biến thiên:
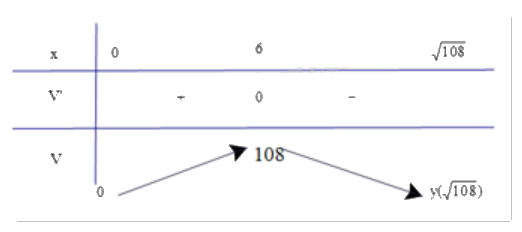
Do đó, thể tích của hình hộp là lớn nhất khi độ dài cạnh đáy \(x = 6\) cm.
Khi đó, chiều cao của hình hộp là: \(\frac{{108 - {6^2}}}{{4.6}} = 3\left( {cm} \right)\).
Giải Bài Tập 1.14 Trang 19 Toán 12 Tập 1 - Kết Nối Tri Thức: Chi Tiết và Dễ Hiểu
Bài tập 1.14 trang 19 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu chúng ta tính giới hạn của hàm số khi x tiến tới một giá trị nhất định. Để giải bài tập này, chúng ta cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, cũng như các phương pháp tính giới hạn thường gặp.
Đề Bài Bài Tập 1.14
(Đề bài cụ thể của bài tập 1.14 sẽ được chèn vào đây. Ví dụ: Tính các giới hạn sau: a) lim (x->2) (x^2 - 4) / (x - 2); b) lim (x->0) sin(x) / x)
Lời Giải Chi Tiết
Để giải bài tập này, chúng ta sẽ áp dụng các bước sau:
- Phân tích hàm số: Xác định dạng của hàm số và tìm cách đơn giản hóa biểu thức.
- Áp dụng định nghĩa giới hạn: Sử dụng định nghĩa giới hạn để tính giới hạn của hàm số.
- Sử dụng các tính chất của giới hạn: Áp dụng các tính chất của giới hạn để đơn giản hóa quá trình tính toán.
- Kiểm tra kết quả: Đảm bảo kết quả tính toán là chính xác và hợp lý.
Giải Chi Tiết Từng Phần (Ví dụ với đề bài giả định ở trên)
a) lim (x->2) (x^2 - 4) / (x - 2)
Ta có thể phân tích tử số thành (x - 2)(x + 2). Khi đó:
lim (x->2) (x^2 - 4) / (x - 2) = lim (x->2) (x - 2)(x + 2) / (x - 2) = lim (x->2) (x + 2) = 2 + 2 = 4
b) lim (x->0) sin(x) / x
Đây là một giới hạn lượng giác cơ bản. Ta biết rằng lim (x->0) sin(x) / x = 1
Lưu Ý Quan Trọng
- Khi tính giới hạn, cần chú ý đến các trường hợp đặc biệt như dạng vô định (0/0, ∞/∞).
- Sử dụng các công thức giới hạn lượng giác và các định lý giới hạn để đơn giản hóa quá trình tính toán.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Bài tập 1.15 trang 19 SGK Toán 12 tập 1 Kết nối tri thức
- Bài tập 1.16 trang 19 SGK Toán 12 tập 1 Kết nối tri thức
Kết Luận
Bài tập 1.14 trang 19 SGK Toán 12 tập 1 Kết nối tri thức là một bài tập quan trọng giúp các em hiểu rõ hơn về khái niệm giới hạn hàm số. Hy vọng với lời giải chi tiết và dễ hiểu này, các em sẽ tự tin hơn trong việc giải các bài tập tương tự và đạt kết quả tốt trong môn Toán 12.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi trong phần bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ các em!