Lý thuyết Đường tiệm cận của đồ thị hàm số Toán 12 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Đường Tiệm Cận Đồ Thị Hàm Số Toán 12 Kết Nối Tri Thức
Đường tiệm cận là một khái niệm quan trọng trong chương trình Toán 12 Kết Nối Tri Thức, giúp học sinh hiểu rõ hơn về hành vi của đồ thị hàm số khi x hoặc y tiến tới vô cùng. Nắm vững lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến đồ thị hàm số một cách hiệu quả.
Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu về lý thuyết đường tiệm cận, bao gồm định nghĩa, các loại đường tiệm cận và phương pháp tìm đường tiệm cận của các hàm số thường gặp.
1. Đường tiệm cận ngang
1. Đường tiệm cận ngang
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\) |
Ví dụ: Tìm TCN của đồ thị hàm số \(y = f(x) = \frac{{3x - 2}}{{x + 1}}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\)
Vậy đồ thị hàm số f(x) có TCN là y = 3.
2. Đường tiệm cận đứng
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \); |
Ví dụ: Tìm TCĐ của đồ thị hàm số \(y = f(x) = \frac{{3 - x}}{{x + 2}}\)
Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3 - x}}{{x + 2}} = + \infty \)
Vậy đồ thị hàm số có TCĐ là x = -2
3.Đường tiệm cận xiên
Đường thẳng \(y = ax + b(a \ne 0)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) |
Ví dụ: Tìm TCX của đồ thị hàm số \(y = f(x) = x + \frac{1}{{x + 2}}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 2}} = 0\)
Vậy đồ thị hàm số có TCX là y = x
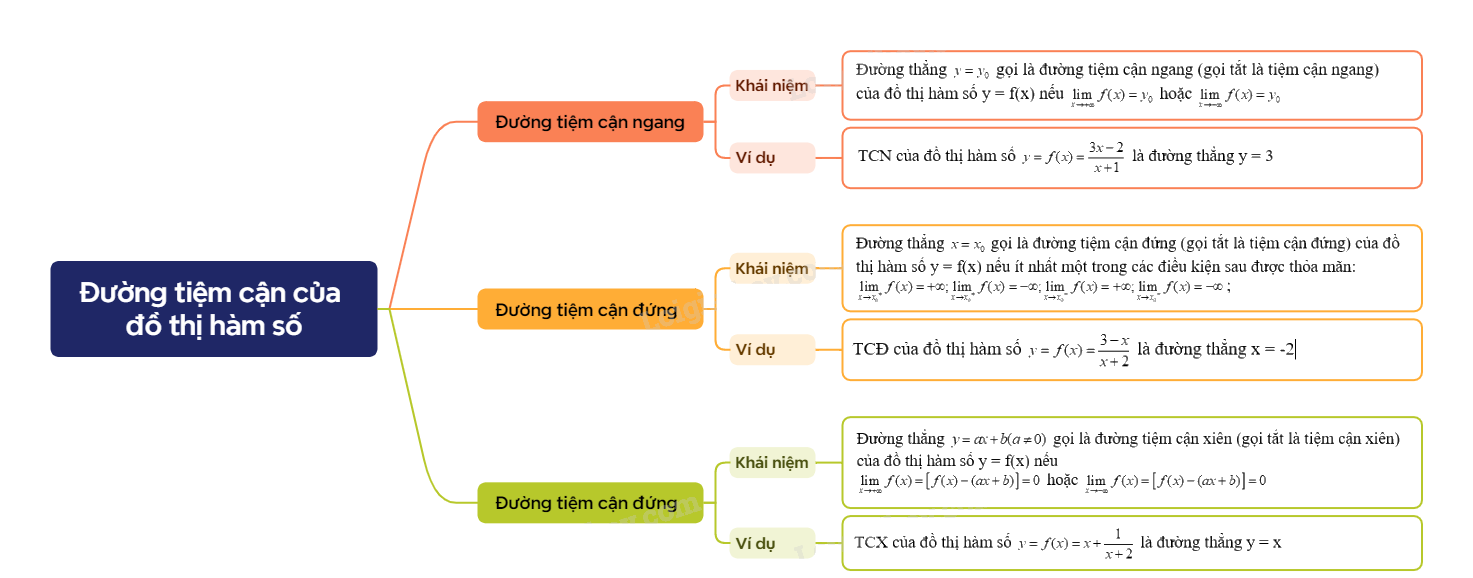
Lý Thuyết Đường Tiệm Cận Đồ Thị Hàm Số Toán 12 Kết Nối Tri Thức
Đường tiệm cận đóng vai trò then chốt trong việc phân tích và vẽ đồ thị hàm số. Hiểu rõ về đường tiệm cận giúp ta dự đoán được xu hướng của đồ thị khi biến số độc lập tiến tới một giá trị cụ thể hoặc vô cùng.
1. Định Nghĩa Đường Tiệm Cận
Đường tiệm cận của đồ thị hàm số y = f(x) là đường thẳng mà đồ thị của hàm số đó tiến gần đến khi x hoặc y tiến tới vô cùng hoặc một giá trị nhất định.
2. Các Loại Đường Tiệm Cận
- Tiệm Cận Đứng: Đường thẳng x = a là tiệm cận đứng của đồ thị hàm số y = f(x) nếu limx→a+ f(x) = ±∞ hoặc limx→a- f(x) = ±∞.
- Tiệm Cận Ngang: Đường thẳng y = b là tiệm cận ngang của đồ thị hàm số y = f(x) nếu limx→+∞ f(x) = b hoặc limx→-∞ f(x) = b.
- Tiệm Cận Xiên: Đường thẳng y = ax + b (với a ≠ 0) là tiệm cận xiên của đồ thị hàm số y = f(x) nếu limx→+∞ [f(x) - (ax + b)] = 0 hoặc limx→-∞ [f(x) - (ax + b)] = 0.
3. Phương Pháp Tìm Đường Tiệm Cận
a. Tiệm Cận Đứng
Để tìm tiệm cận đứng, ta tìm các giá trị x sao cho mẫu số của hàm số bằng 0 và tử số khác 0.
Ví dụ: Hàm số y = 1/(x-2). Mẫu số bằng 0 khi x = 2. Vậy đường tiệm cận đứng là x = 2.
b. Tiệm Cận Ngang
Để tìm tiệm cận ngang, ta tính giới hạn của hàm số khi x tiến tới vô cùng và âm vô cùng.
Ví dụ: Hàm số y = (2x + 1)/(x - 1). limx→+∞ (2x + 1)/(x - 1) = 2. Vậy đường tiệm cận ngang là y = 2.
c. Tiệm Cận Xiên
Để tìm tiệm cận xiên, ta thực hiện các bước sau:
- Tính a = limx→+∞ f(x)/x hoặc limx→-∞ f(x)/x.
- Tính b = limx→+∞ [f(x) - ax] hoặc limx→-∞ [f(x) - ax].
- Đường tiệm cận xiên có phương trình y = ax + b.
Ví dụ: Hàm số y = (x2 + 1)/x. a = limx→+∞ (x2 + 1)/x = +∞. Do đó, hàm số không có tiệm cận xiên.
4. Bài Tập Vận Dụng
Tìm đường tiệm cận của các hàm số sau:
- y = (x + 3)/(x - 1)
- y = (2x2 - 1)/(x2 + 2)
- y = (x3)/(x2 - 4)
5. Lưu Ý Quan Trọng
Không phải hàm số nào cũng có đường tiệm cận. Một hàm số có thể có một, hai hoặc ba loại đường tiệm cận khác nhau. Việc xác định đúng loại đường tiệm cận và phương trình của nó là rất quan trọng để vẽ đồ thị hàm số chính xác.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết đường tiệm cận của đồ thị hàm số Toán 12 Kết Nối Tri Thức. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức này nhé!