Giải bài tập 16 trang 92 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 16 Trang 92 Toán 12 Tập 2 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 16 trang 92 SGK Toán 12 tập 2 - Kết nối tri thức trên tusach.vn. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và nắm vững kiến thức liên quan đến bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) \(y = {x^3} - 3{x^2}\); b) \(y = \frac{{2x + 1}}{{x + 2}}\); c) \(y = \frac{{2{x^2} + x - 2}}{{x - 1}}\).
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = {x^3} - 3{x^2}\);
b) \(y = \frac{{2x + 1}}{{x + 2}}\);
c) \(y = \frac{{2{x^2} + x - 2}}{{x - 1}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số để khảo sát và vẽ đồ thị hàm số:
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực. Chỉ ra các đường tiệm cận (nếu có) của đồ thị hàm số
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết
a) 1. Tập xác định: \(D = \mathbb{R}\).
2. Sự biến thiên:
Ta có: \(y' = 3{x^2} - 6x,y' = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\)
Trên khoảng \(\left( {0;2} \right)\), \(y' < 0\) nên hàm số nghịch biến. Trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến trên mỗi khoảng đó.
Hàm số đạt cực đại tại \(x = 0\), giá trị cực đại . Hàm số đạt cực tiểu tại \(x = 2\), giá trị cực tiểu \({y_{CT}} = - 4\).
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} - 3x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^3}\left( {1 - \frac{3}{x}} \right)} \right] = - \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} - 3x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^3}\left( {1 - \frac{3}{x}} \right)} \right] = + \infty \)
Bảng biến thiên:

3. Đồ thị:
Giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2}\) với trục tung là (0; 0). \({x^3} - 3{x^2} = 0 \Leftrightarrow {x^2}\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.\) Giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2}\) với trục hoành là (0; 0); (3; 0) Đồ thị hàm số có tâm đối xứng là điểm \(\left( {1; - 2} \right)\). |

b) 1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ { - 2} \right\}\)
2. Sự biến thiên:
\(y' = \frac{3}{{{{\left( {x + 2} \right)}^2}}} > 0\forall x \ne - 2\)
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x + 2}} = 2;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 1}}{{x + 2}} = 2\). \(\mathop {\lim }\limits_{x \to - {2^ - }} y = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{2x + 1}}{{x + 2}} = + \infty ;\mathop {\lim }\limits_{x \to - {2^ + }} y = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{2x + 1}}{{x + 2}} = - \infty \).
Do đó, đồ thị hàm số nhận đường thẳng \(x = - 2\) làm tiệm cận đứng và đường thẳng \(y = 2\) làm tiệm cận ngang.
Bảng biến thiên:

3. Đồ thị: Giao điểm của đồ thị hàm số với trục tung là \(\left( {0;\frac{1}{2}} \right)\).
\(y = 0 \Leftrightarrow \frac{{2x + 1}}{{x + 2}} = 0 \Leftrightarrow x = \frac{{ - 1}}{2}\)
Giao điểm của đồ thị hàm số với trục hoành là \(\left( {\frac{{ - 1}}{2};0} \right)\).
Đồ thị hàm số nhận giao điểm \(I\left( { - 2;2} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.

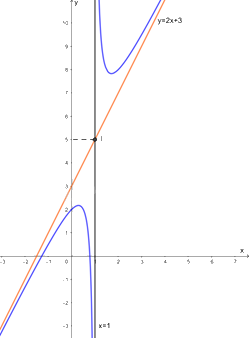
c) 1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ 1 \right\}\)
2. Sự biến thiên:
Ta có: \(y = \frac{{2{x^2} + x - 2}}{{x - 1}} = 2x + 3 + \frac{1}{{x - 1}}\)
\(y' = 2 - \frac{1}{{{{\left( {x - 1} \right)}^2}}},y' = 0 \Leftrightarrow x = \frac{{\sqrt 2 + 2}}{2}\) hoặc \(x = \frac{{ - \sqrt 2 + 2}}{2}\)
Trong khoảng \(\left( { - \infty ;\frac{{ - \sqrt 2 + 2}}{2}} \right)\) và \(\left( {\frac{{\sqrt 2 + 2}}{2}; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Trong khoảng \(\left( {\frac{{ - \sqrt 2 + 2}}{2};1} \right)\) và \(\left( {1;\frac{{\sqrt 2 + 2}}{2}} \right)\), \(y' < 0\) nên hàm số nghịch biến.
Hàm số đạt cực đại tại \(x = \frac{{ - \sqrt 2 + 2}}{2}\), giá trị cực đại .
Hàm số đạt cực tiểu tại \(x = \frac{{2 + \sqrt 2 }}{2}\), giá trị cực đại \({y_{CT}} = 5 + 2\sqrt 2 \).
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} + x - 2}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} + x - 2}}{{x - 1}} = - \infty \) \(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{2{x^2} + x - 2}}{{x - 1}} = - \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2{x^2} + x - 2}}{{x - 1}} = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {2x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( {2x + 3 + \frac{1}{{x - 1}} - \left( {2x + 3} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 1}} = 0\)
\(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {2x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {2x + 3 + \frac{1}{{x - 1}} - \left( {2x + 3} \right)} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 1}} = 0\)
Do đó, đồ thị hàm số nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = 2x + 3\) làm tiệm cận xiên.
Bảng biến thiên:

3. Đồ thị: Giao điểm của đồ thị hàm số với trục tung là \[\left( {0; - 2} \right).\]
\(\frac{{2{x^2} + x - 2}}{{x - 1}} = 0 \Leftrightarrow x = \frac{{ - 1 - \sqrt {17} }}{4}\) hoặc \(x = \frac{{ - 1 + \sqrt {17} }}{4}\)
Giao điểm của đồ thị hàm số với trục hoành là \(\left( {\frac{{ - 1 - \sqrt {17} }}{4};0} \right)\) và \(\left( {\frac{{ - 1 + \sqrt {17} }}{4};0} \right)\)
Đồ thị hàm số nhận giao điểm \[I\left( {1;5} \right)\] của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Giải Bài Tập 16 Trang 92 Toán 12 Tập 2 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 16 trang 92 SGK Toán 12 tập 2 - Kết nối tri thức thuộc chương trình học về tích phân. Đây là một dạng bài tập quan trọng, thường xuyên xuất hiện trong các đề thi. Để giải quyết bài tập này một cách hiệu quả, các em cần nắm vững các kiến thức cơ bản về tích phân, bao gồm:
- Định nghĩa tích phân: Hiểu rõ khái niệm tích phân, tích phân bất định và tích phân xác định.
- Nguyên hàm: Biết cách tìm nguyên hàm của một hàm số.
- Các phương pháp tính tích phân: Nắm vững các phương pháp tính tích phân như đổi biến số, tích phân từng phần.
- Ứng dụng của tích phân: Hiểu cách sử dụng tích phân để tính diện tích, thể tích và các đại lượng khác.
Nội Dung Bài Tập 16 Trang 92
Bài tập 16 thường yêu cầu tính tích phân xác định của một hàm số trên một khoảng cho trước. Để giải bài tập này, các em có thể thực hiện theo các bước sau:
- Tìm nguyên hàm: Tìm nguyên hàm F(x) của hàm số f(x).
- Tính giá trị của nguyên hàm tại cận trên và cận dưới: Tính F(b) và F(a), trong đó b là cận trên và a là cận dưới của tích phân.
- Tính hiệu: Tính hiệu F(b) - F(a). Kết quả này chính là giá trị của tích phân xác định.
Ví Dụ Minh Họa
Giả sử bài tập yêu cầu tính tích phân ∫01 x2 dx. Ta thực hiện như sau:
- Tìm nguyên hàm: Nguyên hàm của x2 là (1/3)x3.
- Tính giá trị của nguyên hàm tại cận trên và cận dưới:
- F(1) = (1/3)(1)3 = 1/3
- F(0) = (1/3)(0)3 = 0
- Tính hiệu: F(1) - F(0) = 1/3 - 0 = 1/3. Vậy, ∫01 x2 dx = 1/3.
Lưu Ý Quan Trọng
Khi giải bài tập tích phân, các em cần chú ý đến các dấu và giới hạn tích phân. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn - Đồng Hành Cùng Học Sinh
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng và lời giải bài tập môn Toán 12. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất!
Bảng Tóm Tắt Các Công Thức Tích Phân Quan Trọng
| Công Thức | Mô Tả |
|---|---|
| ∫ xn dx = (1/(n+1))xn+1 + C | Tích phân của x mũ n |
| ∫ sin(x) dx = -cos(x) + C | Tích phân của sin(x) |
| ∫ cos(x) dx = sin(x) + C | Tích phân của cos(x) |
Hy vọng bài viết này sẽ giúp các em giải quyết bài tập 16 trang 92 SGK Toán 12 tập 2 - Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc các em học tốt!