Giải bài tập 5.23 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 5.23 Trang 53 Toán 12 Tập 2 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 2 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 5.23 trang 53 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S. ABCD, có đáy là hình vuông với cạnh dài 230m, các cạnh bên bằng nhau và dài 219m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC).
Đề bài
Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S. ABCD, có đáy là hình vuông với cạnh dài 230m, các cạnh bên bằng nhau và dài 219m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC).

Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)
Lời giải chi tiết
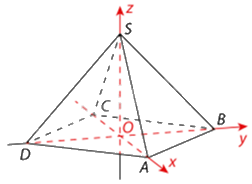
Gọi O là giao điểm của AC và BD, khi đó ta tính được \(OA = OB = OC = OD = 115\sqrt 2 \)
Vì \(SA = SB = SC = SD\) nên tam giác SAC và SBD là các tam giác cân tại S. Do đó, SO vừa là đường trung tuyến vừa là đường cao của các tam giác SAC và SBD. Do đó, \(SO \bot AC,SO \bot BD\) nên \(SO \bot \left( {ABCD} \right)\).
Tam giác SOA vuông tại O nên \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{{219}^2} - {{\left( {115\sqrt 2 } \right)}^2}} = 7\sqrt {439} \)
Chọn hệ trục tọa độ Oxyz có gốc tọa độ trùng với O như hình vẽ.
Khi đó, \(S\left( {0;0;7\sqrt {439} } \right),A\left( {115\sqrt 2 ;0;0} \right);B\left( {0;115\sqrt 2 ;0} \right),C\left( { - 115\sqrt 2 ;0;0} \right)\)
Suy ra: \(\overrightarrow {SA} \left( {115\sqrt 2 ;0; - 7\sqrt {439} } \right),\overrightarrow {AB} \left( { - 115\sqrt 2 ;115\sqrt 2 ;0} \right) \Rightarrow \overrightarrow m = \frac{1}{{115\sqrt 2 }}\overrightarrow {AB} = \left( { - 1;1;0} \right)\),
\(,\overrightarrow {SB} \left( {0;115\sqrt 2 ; - 7\sqrt {439} } \right)\), \(\overrightarrow {BC} \left( { - 115\sqrt 2 ; - 115\sqrt 2 ;0} \right) \Rightarrow \overrightarrow v = \frac{1}{{ - 115\sqrt 2 }}\overrightarrow {BC} = \left( {1;1;0} \right)\)
\(\left[ {\overrightarrow {SA} ,\overrightarrow m } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 7\sqrt {439} }\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 7\sqrt {439} }&{115\sqrt 2 }\\0&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{115\sqrt 2 }&0\\{ - 1}&1\end{array}} \right|} \right)\)\( = \left( {7\sqrt {439} ;7\sqrt {439} ;115\sqrt 2 } \right)\)
Mặt phẳng (SAB) nhận \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {SA} ,\overrightarrow m } \right] = \left( {7\sqrt {439} ;7\sqrt {439} ;115\sqrt 2 } \right)\) làm vectơ pháp tuyến.
\(\left[ {\overrightarrow {SB} ,\overrightarrow v } \right] = \left( {\left| {\begin{array}{*{20}{c}}{115\sqrt 2 }&{ - 7\sqrt {439} }\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 7\sqrt {439} }&0\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{115\sqrt 2 }\\1&1\end{array}} \right|} \right)\)\( = \left( {7\sqrt {439} ; - 7\sqrt {439} ; - 115\sqrt 2 } \right)\)
Mặt phẳng (SBC) nhận \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {SB} ,\overrightarrow v } \right] = \left( {7\sqrt {439} ; - 7\sqrt {439} ; - 115\sqrt 2 } \right)\) làm vectơ pháp tuyến.
Ta có: \(\left( {\left( {SAB} \right),\left( {SBC} \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\)
\( = \frac{{\left| {{{\left( {7\sqrt {439} } \right)}^2} - {{\left( {7\sqrt {439} } \right)}^2} - {{\left( {115\sqrt 2 } \right)}^2}} \right|}}{{\sqrt {{{\left( {7\sqrt {439} } \right)}^2} + {{\left( {7\sqrt {439} } \right)}^2} + {{\left( {115\sqrt 2 } \right)}^2}} .\sqrt {{{\left( {7\sqrt {439} } \right)}^2} + {{\left( { - 7\sqrt {439} } \right)}^2} + {{\left( { - 115\sqrt 2 } \right)}^2}} }}\)
\( = \frac{{{{\left( {115\sqrt 2 } \right)}^2}}}{{69\;472}} = \frac{{13225}}{{34736}} \Rightarrow \left( {\left( {SAB} \right),\left( {SBC} \right)} \right) \approx 67,{6^o}\)
Vậy góc giữa hai mặt phẳng (SAB) và (SBC) bằng \(67,{6^o}\).
Giải Bài Tập 5.23 Trang 53 Toán 12 Tập 2 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 5.23 trang 53 SGK Toán 12 tập 2 Kết nối tri thức thuộc chương trình học về Đạo hàm của hàm số hợp. Để giải bài tập này, chúng ta cần nắm vững các kiến thức về quy tắc đạo hàm của hàm hợp, đạo hàm của các hàm số cơ bản và các kỹ năng biến đổi đại số.
Nội dung bài tập 5.23:
(Đề bài cụ thể của bài tập 5.23 sẽ được trình bày tại đây. Ví dụ: Cho hàm số y = f(x) = sin(x^2 + 1). Tính f'(x).)
Lời giải chi tiết:
Để giải bài tập này, ta áp dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x)
- Xác định hàm u(v) và v(x): Trong trường hợp này, ta có u(v) = sin(v) và v(x) = x^2 + 1.
- Tính đạo hàm của u(v) và v(x):
- u'(v) = cos(v)
- v'(x) = 2x
- Áp dụng quy tắc đạo hàm hàm hợp:
f'(x) = u'(v(x)) * v'(x) = cos(x^2 + 1) * 2x = 2x * cos(x^2 + 1)
Kết luận:
Vậy, đạo hàm của hàm số y = f(x) = sin(x^2 + 1) là f'(x) = 2x * cos(x^2 + 1).
Các dạng bài tập tương tự và phương pháp giải
Ngoài bài tập 5.23, chương trình học về đạo hàm hàm hợp còn có nhiều dạng bài tập khác. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
- Dạng 1: Đạo hàm của hàm hợp nhiều lớp: Ví dụ: y = cos(sin(x)). Cần áp dụng quy tắc đạo hàm hàm hợp nhiều lần.
- Dạng 2: Đạo hàm của hàm số có chứa căn thức: Ví dụ: y = √(x^2 + 1). Cần biến đổi căn thức về dạng lũy thừa trước khi áp dụng quy tắc đạo hàm.
- Dạng 3: Đạo hàm của hàm số có chứa hàm mũ và logarit: Ví dụ: y = e^(x^2). Cần sử dụng các công thức đạo hàm của hàm mũ và logarit.
Mẹo giải nhanh:
Để giải nhanh các bài tập về đạo hàm hàm hợp, bạn nên:
- Nắm vững quy tắc đạo hàm hàm hợp.
- Thực hành nhiều bài tập để làm quen với các dạng bài khác nhau.
- Sử dụng các công thức đạo hàm cơ bản một cách linh hoạt.
Bài tập luyện tập:
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
- Tính đạo hàm của hàm số y = tan(x^3).
- Tính đạo hàm của hàm số y = e^(sin(x)).
- Tính đạo hàm của hàm số y = ln(x^2 + 1).
tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, bạn đã có thể hiểu rõ cách giải bài tập 5.23 trang 53 SGK Toán 12 tập 2 Kết nối tri thức. Chúc bạn học tập tốt!
| Công thức | Mô tả |
|---|---|
| (u(v(x)))' | Đạo hàm của hàm hợp |
| u'(v(x)) * v'(x) | Công thức tính đạo hàm hàm hợp |