Giải bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 1.9 Trang 14 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.9 trang 14 SGK Toán 12 tập 1 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các tài liệu học tập hữu ích khác.
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số (fleft( t right) = frac{{5;000}}{{1 + 5{e^{ - t}}}},t ge 0,) trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Đề bài
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = \frac{{5\;000}}{{1 + 5{e^{ - t}}}},t \ge 0,\) trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết
Ta có: \(f'\left( t \right) = \frac{{ - 5000\left( {1 + 5{e^{ - t}}} \right)'}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}} = \frac{{25\;000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\)
Tốc độ bán hàng là lớn nhất khi \(f'\left( t \right)\) lớn nhất.
Đặt \(h\left( t \right) = \frac{{25\;000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\).
\(h'\left( t \right) = \frac{{ - 25\;000{e^{ - t}}{{\left( {1 + 5{e^{ - t}}} \right)}^2} - 2.\left( { - 5{e^{ - t}}} \right).\left( {1 + 5{e^{ - t}}} \right).25\;000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}}\)
\( = \frac{{ - 25\;000{e^{ - t}}\left( {1 + 5{e^{ - t}}} \right)\left( {1 + 5{e^{ - t}} - 10{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}} = \frac{{ - 25\;000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}}\)
\(h'\left( t \right) = 0 \Leftrightarrow \frac{{ - 25\;000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}} = 0 \Leftrightarrow 1 - 5{e^{ - t}} = 0 \Leftrightarrow {e^{ - t}} = \frac{1}{5} \Leftrightarrow t = \ln 5\) (tm)
Ta có bảng biến thiên với \(t \in \left[ {0; + \infty } \right)\):
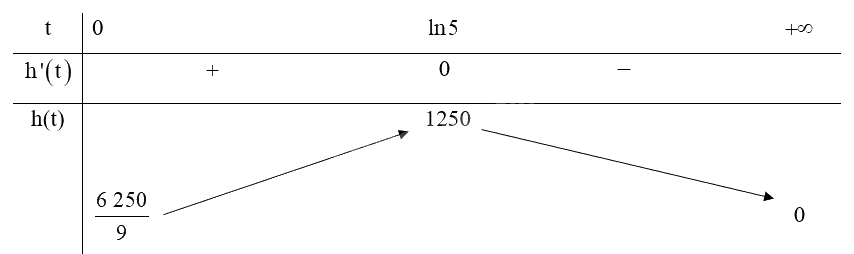
Vậy sau khi phát hành khoảng \(\ln 5 \approx 1,6\) năm thì thì tốc độ bán hàng là lớn nhất.
Giải Bài Tập 1.9 Trang 14 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 1.9 trang 14 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu chúng ta vận dụng kiến thức về đạo hàm của hàm số để giải quyết một bài toán cụ thể. Để hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích đề bài, xác định các bước giải và đưa ra lời giải chi tiết.
Đề Bài:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Lời Giải:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính đạo hàm cấp một của hàm số.
- Bước 3: Tìm các điểm làm đạo hàm cấp một bằng 0.
- Bước 4: Lập bảng biến thiên của hàm số.
- Bước 5: Kết luận về các điểm cực trị.
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
f'(x) = 3x2 - 6x
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
⇔ x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Dựa vào bảng biến thiên, ta thấy:
Lưu Ý Quan Trọng:
Khi giải các bài toán về cực trị của hàm số, cần lưu ý các bước sau:
- Xác định đúng tập xác định của hàm số.
- Tính đạo hàm cấp một một cách chính xác.
- Giải phương trình f'(x) = 0 để tìm các điểm nghi ngờ là cực trị.
- Lập bảng biến thiên hoặc sử dụng dấu của đạo hàm cấp một để xác định loại cực trị.
Bài Tập Tương Tự:
Để củng cố kiến thức về cực trị của hàm số, các em có thể tự giải các bài tập sau:
- Bài 1.10 trang 14 SGK Toán 12 tập 1 Kết nối tri thức.
- Bài 1.11 trang 15 SGK Toán 12 tập 1 Kết nối tri thức.
Tổng Kết:
Bài tập 1.9 trang 14 SGK Toán 12 tập 1 Kết nối tri thức là một bài tập cơ bản về cực trị của hàm số. Việc nắm vững các bước giải và các lưu ý quan trọng sẽ giúp các em tự tin giải quyết các bài toán tương tự trong các kỳ thi sắp tới. Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp ích cho các em trong quá trình học tập.