Giải Bài Tập 2.28 Trang 73 Toán 12 Tập 1 - Kết Nối Tri Thức

Giải bài tập 2.28 trang 73 SGK Toán 12 tập 1 - Kết nối tri thức

Giải Bài Tập 2.28 Trang 73 Toán 12 Tập 1 - Kết Nối Tri Thức

Bài tập 2.28 trang 73 SGK Toán 12 tập 1 - Kết nối tri thức là một bài toán quan trọng trong chương trình học. Bài viết này của tusach.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải toán.

Chúng tôi sẽ trình bày đầy đủ các bước giải, phân tích rõ ràng từng bước để các em có thể tự tin áp dụng vào các bài tập tương tự.

Cho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằng A. \(\frac{{{a^2}}}{4}\). B. \(\frac{{{a^2}}}{2}\). C. \(\frac{{{a^2}}}{3}\). D. \({a^2}\).

Đề bài

Cho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằngA. \(\frac{{{a^2}}}{4}\).B. \(\frac{{{a^2}}}{2}\).C. \(\frac{{{a^2}}}{3}\).D. \({a^2}\).

Phương pháp giải - Xem chi tiết Giải bài tập 2.28 trang 73 SGK Toán 12 tập 1 - Kết nối tri thức 1

Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).

Lời giải chi tiết

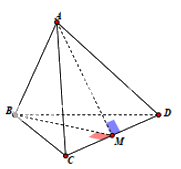
Giải bài tập 2.28 trang 73 SGK Toán 12 tập 1 - Kết nối tri thức 2

Tam giác ACD có ba cạnh bằng a nên tam giác ACD đều, AM là đường trung tuyến đồng thời là đường cao nên \(AM = \frac{{a\sqrt 3 }}{2}\).

Tam giác CBD có ba cạnh bằng a nên tam giác CBD đều, BM là đường trung tuyến đồng thời là đường cao nên \(BM = \frac{{a\sqrt 3 }}{2}\).

Áp dụng định côsin vào tam giác ABM ta có:

\(\cos \widehat {BAM} = \frac{{A{M^2} + A{B^2} - M{B^2}}}{{2AB.MB}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {a^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}{{2.\frac{{a\sqrt 3 }}{2}.a}} = \frac{{\sqrt 3 }}{3}\)

\(\overrightarrow {AB} .\overrightarrow {AM} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AM} } \right) = a.\frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{3} = \frac{{{a^2}}}{2}\)

Chọn B

Giải Bài Tập 2.28 Trang 73 SGK Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết

Bài tập 2.28 trang 73 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết. Dưới đây là lời giải chi tiết và các lưu ý quan trọng:

Đề Bài

Cho hàm số y = f(x) = x³ - 3x² + 2. Hãy tính f'(x) và tìm các điểm cực trị của hàm số.

Lời Giải Chi Tiết

Tính đạo hàm f'(x):

Sử dụng quy tắc đạo hàm của tổng và lũy thừa, ta có:

f'(x) = 3x² - 6x

Tìm các điểm cực trị:

Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:

3x² - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2

Xác định loại cực trị:

Ta xét dấu của f'(x) trên các khoảng:

Khoảng (-∞, 0): Chọn x = -1, f'(-1) = 3(-1)² - 6(-1) = 9 > 0, hàm số đồng biến.
Khoảng (0, 2): Chọn x = 1, f'(1) = 3(1)² - 6(1) = -3 < 0, hàm số nghịch biến.
Khoảng (2, +∞): Chọn x = 3, f'(3) = 3(3)² - 6(3) = 9 > 0, hàm số đồng biến.

Vậy:

Tại x = 0, hàm số đạt cực đại. Giá trị cực đại là f(0) = 0³ - 3(0)² + 2 = 2.
Tại x = 2, hàm số đạt cực tiểu. Giá trị cực tiểu là f(2) = 2³ - 3(2)² + 2 = 0.

Kết Luận

Hàm số y = f(x) = x³ - 3x² + 2 đạt cực đại tại điểm (0, 2) và đạt cực tiểu tại điểm (2, 0).

Lưu Ý Quan Trọng

Luôn kiểm tra lại các bước tính đạo hàm để tránh sai sót.
Khi xét dấu của đạo hàm, chọn các điểm đại diện trong từng khoảng để đảm bảo tính chính xác.
Hiểu rõ ý nghĩa của đạo hàm trong việc xác định tính đơn điệu và cực trị của hàm số.

Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK và sách bài tập Toán 12 tập 1 - Kết nối tri thức.

Tusach.vn - Đồng Hành Cùng Học Sinh

Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1 - Kết nối tri thức. Hãy truy cập tusach.vn để học Toán 12 hiệu quả hơn!

Điểm	Giá trị
Cực đại	(0, 2)
Cực tiểu	(2, 0)
Bảng tóm tắt các điểm cực trị

Giải bài tập 2.28 trang 73 SGK Toán 12 tập 1 - Kết nối tri thức