Giải mục 3 trang 8,9,10 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Mục 3 Trang 8,9,10 SGK Toán 12 Tập 2 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết Mục 3 trang 8,9,10 SGK Toán 12 tập 2 - Kết Nối Tri Thức trên tusach.vn. Chúng tôi hiểu rằng việc tự học và làm bài tập đôi khi gặp nhiều khó khăn.
Do đó, đội ngũ giáo viên giàu kinh nghiệm của tusach.vn đã biên soạn bộ giải bài tập này với mục đích giúp các em hiểu rõ bản chất bài học, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi.
Nguyên hàm của một số hàm số thường gặp
?
Trả lời câu hỏi ? trang 8 SGK Toán 12 Kết nối tri thức
Bằng cách viết lại các hàm số sau dưới dạng lũy thừa \(y = {x^\alpha }\left( {x > 0} \right)\), hãy tính đạo hàm của các hàm số sau với \(x > 0\): \(y = \frac{1}{{{x^4}}},y = {x^{\sqrt 2 }},y = \frac{1}{{\sqrt[3]{x}}}\).
Phương pháp giải:
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
Ta có: \(y = \frac{1}{{{x^4}}} = {x^{ - 4}}\) nên \(y' = - 4{x^{ - 5}}\); \(y = {x^{\sqrt 2 }} = {x^{\frac{1}{2}}}\) nên \(y' = \frac{1}{2}{x^{ - \frac{1}{2}}} = \frac{1}{{2\sqrt x }}\), \(y = \frac{1}{{\sqrt[3]{x}}} = {x^{\frac{{ - 1}}{3}}}\) nên \(y' = \frac{{ - 1}}{3}{x^{\frac{{ - 4}}{3}}} = \frac{{ - 1}}{{3{x^{\frac{4}{3}}}}}\).
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 8 SGK Toán 12 Kết nối tri thức
a) Với \(\alpha \ne - 1\), tính đạo hàm của hàm số \(y = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}\left( {x > 0} \right)\).
b) Cho hàm số \(y = \ln \left| x \right|\left( {x \ne 0} \right)\). Tính đạo hàm của hàm số này trong hai trường hợp: \(x > 0\) và \(x < 0\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
a) Vì \(y' = {\left( {\frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} \right)'} = \frac{{\left( {\alpha + 1} \right){x^\alpha }}}{{\alpha + 1}} = {x^\alpha }\) với mọi \(x > 0\), \(\alpha \ne - 1\).
b) Ta có: \(y' = \left( {\ln \left| x \right|} \right)' = \frac{1}{{\left| x \right|}}\).
Với \(x > 0\) thì \(y' = \frac{1}{x}\).
Với \(x < 0\) thì \(y' = \frac{1}{{ - x}}\).
LT5
Trả lời câu hỏi Luyện tập 5 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\frac{1}{{{x^4}}}dx} \);
b) \(\int {x\sqrt x dx\left( {x > 0} \right)} \);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx\left( {x > 0} \right)} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lũy thừa để tính:
\(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\left( {\alpha \ne - 1} \right)\)
Lời giải chi tiết:
a) \(\int {\frac{1}{{{x^4}}}dx} = \int {{x^{ - 4}}dx} = \frac{{{x^{ - 4 + 1}}}}{{ - 4 + 1}} + C = \frac{{{x^{ - 3}}}}{{ - 3}} + C = \frac{{ - 1}}{{3{x^3}}} + C\);
b) \(\int {x\sqrt x dx = } \int {{x^{\frac{3}{2}}}dx = } \frac{{{x^{\frac{3}{2} + 1}}}}{{\frac{3}{2} + 1}} + C = \frac{2}{5}{x^2}\sqrt x + C\);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx = \int {\frac{3}{x}dx - \int {5\sqrt[3]{x}} dx = 3\int {\frac{1}{x}dx - 5\int {{x^{\frac{1}{3}}}} dx = 3\ln \left| x \right| - 5.\frac{{{x^{\frac{4}{3}}}}}{{\frac{4}{3}}} + C} } } \)
\( = 3\ln \left| x \right| - \frac{{15x\sqrt[3]{x}}}{4} + C\).
LT6
Trả lời câu hỏi Luyện tập 6 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} \);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lượng giác để tính:
\(\int {\cos x} dx = \sin x + C,\int {\sin x} dx = - \cos x + C,\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C,\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\)
Lời giải chi tiết:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} = 3\int {\cos x} dx - 4\int {\sin x} dx = 3\sin x + 4\cos x + C\);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} = \int {\frac{1}{{{{\cos }^2}x}}} dx - \int {\frac{1}{{{{\sin }^2}x}}} dx = \tan x + \cot x + C\).
LT7
Trả lời câu hỏi Luyện tập 7 trang 10 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {{4^x}dx} \);
b) \(\int {\frac{1}{{{e^x}}}dx} \);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số mũ để tính:
\(\int {{e^x}dx} = {e^x} + C,\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\left( {0 < a \ne 1} \right)\)
Lời giải chi tiết:
a) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\);
b) \(\int {\frac{1}{{{e^x}}}dx} = \int {{{\left( {\frac{1}{e}} \right)}^x}dx} = \frac{{{{\left( {\frac{1}{e}} \right)}^x}}}{{\ln \frac{1}{e}}} + C = - {e^{ - x}} + C\);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} = 2\int {{3^x}} dx - \frac{1}{3}\int {{7^x}} dx = \frac{{{{2.3}^x}}}{{\ln 3}} - \frac{{{7^x}}}{{3\ln 7}} + C\).
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 9 SGK Toán 12 Kết nối tri thức
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
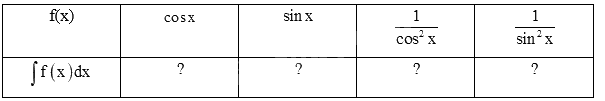
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số lượng giác để tính:
\(\left( {\sin x} \right)' = \cos x,\left( {\cos x} \right)' = - \sin x,\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}},\left( {\cot x} \right)' = \frac{{ - 1}}{{{{\sin }^2}x}}\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)

b)
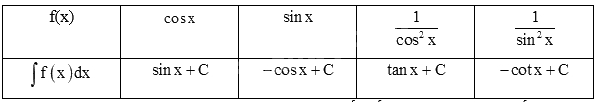
HĐ7
Trả lời câu hỏi Hoạt động 7 trang 10 SGK Toán 12 Kết nối tri thức
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
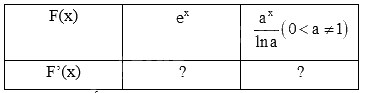
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
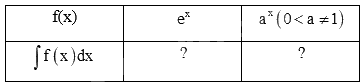
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số mũ để tính: \(\left( {{e^x}} \right)' = {e^x},\left( {{a^x}} \right)' = {a^x}.\ln a\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)
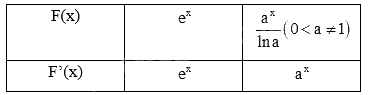
b)

- ?
- HĐ5
- LT5
- HĐ6
- LT6
- HĐ7
- LT7
Trả lời câu hỏi ? trang 8 SGK Toán 12 Kết nối tri thức
Bằng cách viết lại các hàm số sau dưới dạng lũy thừa \(y = {x^\alpha }\left( {x > 0} \right)\), hãy tính đạo hàm của các hàm số sau với \(x > 0\): \(y = \frac{1}{{{x^4}}},y = {x^{\sqrt 2 }},y = \frac{1}{{\sqrt[3]{x}}}\).
Phương pháp giải:
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
Ta có: \(y = \frac{1}{{{x^4}}} = {x^{ - 4}}\) nên \(y' = - 4{x^{ - 5}}\); \(y = {x^{\sqrt 2 }} = {x^{\frac{1}{2}}}\) nên \(y' = \frac{1}{2}{x^{ - \frac{1}{2}}} = \frac{1}{{2\sqrt x }}\), \(y = \frac{1}{{\sqrt[3]{x}}} = {x^{\frac{{ - 1}}{3}}}\) nên \(y' = \frac{{ - 1}}{3}{x^{\frac{{ - 4}}{3}}} = \frac{{ - 1}}{{3{x^{\frac{4}{3}}}}}\).
Trả lời câu hỏi Hoạt động 5 trang 8 SGK Toán 12 Kết nối tri thức
a) Với \(\alpha \ne - 1\), tính đạo hàm của hàm số \(y = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}\left( {x > 0} \right)\).
b) Cho hàm số \(y = \ln \left| x \right|\left( {x \ne 0} \right)\). Tính đạo hàm của hàm số này trong hai trường hợp: \(x > 0\) và \(x < 0\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
a) Vì \(y' = {\left( {\frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} \right)'} = \frac{{\left( {\alpha + 1} \right){x^\alpha }}}{{\alpha + 1}} = {x^\alpha }\) với mọi \(x > 0\), \(\alpha \ne - 1\).
b) Ta có: \(y' = \left( {\ln \left| x \right|} \right)' = \frac{1}{{\left| x \right|}}\).
Với \(x > 0\) thì \(y' = \frac{1}{x}\).
Với \(x < 0\) thì \(y' = \frac{1}{{ - x}}\).
Trả lời câu hỏi Luyện tập 5 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\frac{1}{{{x^4}}}dx} \);
b) \(\int {x\sqrt x dx\left( {x > 0} \right)} \);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx\left( {x > 0} \right)} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lũy thừa để tính:
\(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\left( {\alpha \ne - 1} \right)\)
Lời giải chi tiết:
a) \(\int {\frac{1}{{{x^4}}}dx} = \int {{x^{ - 4}}dx} = \frac{{{x^{ - 4 + 1}}}}{{ - 4 + 1}} + C = \frac{{{x^{ - 3}}}}{{ - 3}} + C = \frac{{ - 1}}{{3{x^3}}} + C\);
b) \(\int {x\sqrt x dx = } \int {{x^{\frac{3}{2}}}dx = } \frac{{{x^{\frac{3}{2} + 1}}}}{{\frac{3}{2} + 1}} + C = \frac{2}{5}{x^2}\sqrt x + C\);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx = \int {\frac{3}{x}dx - \int {5\sqrt[3]{x}} dx = 3\int {\frac{1}{x}dx - 5\int {{x^{\frac{1}{3}}}} dx = 3\ln \left| x \right| - 5.\frac{{{x^{\frac{4}{3}}}}}{{\frac{4}{3}}} + C} } } \)
\( = 3\ln \left| x \right| - \frac{{15x\sqrt[3]{x}}}{4} + C\).
Trả lời câu hỏi Hoạt động 6 trang 9 SGK Toán 12 Kết nối tri thức
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
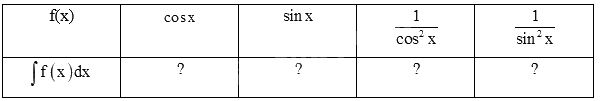
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số lượng giác để tính:
\(\left( {\sin x} \right)' = \cos x,\left( {\cos x} \right)' = - \sin x,\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}},\left( {\cot x} \right)' = \frac{{ - 1}}{{{{\sin }^2}x}}\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)

b)
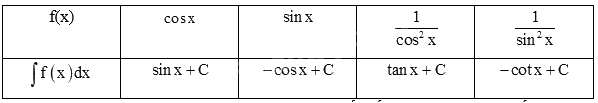
Trả lời câu hỏi Luyện tập 6 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} \);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lượng giác để tính:
\(\int {\cos x} dx = \sin x + C,\int {\sin x} dx = - \cos x + C,\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C,\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\)
Lời giải chi tiết:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} = 3\int {\cos x} dx - 4\int {\sin x} dx = 3\sin x + 4\cos x + C\);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} = \int {\frac{1}{{{{\cos }^2}x}}} dx - \int {\frac{1}{{{{\sin }^2}x}}} dx = \tan x + \cot x + C\).
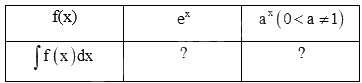
Trả lời câu hỏi Hoạt động 7 trang 10 SGK Toán 12 Kết nối tri thức
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
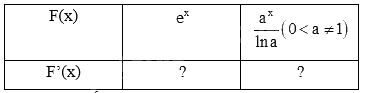
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số mũ để tính: \(\left( {{e^x}} \right)' = {e^x},\left( {{a^x}} \right)' = {a^x}.\ln a\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)
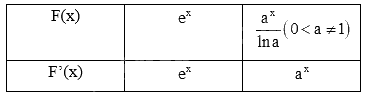
b)

Trả lời câu hỏi Luyện tập 7 trang 10 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {{4^x}dx} \);
b) \(\int {\frac{1}{{{e^x}}}dx} \);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số mũ để tính:
\(\int {{e^x}dx} = {e^x} + C,\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\left( {0 < a \ne 1} \right)\)
Lời giải chi tiết:
a) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\);
b) \(\int {\frac{1}{{{e^x}}}dx} = \int {{{\left( {\frac{1}{e}} \right)}^x}dx} = \frac{{{{\left( {\frac{1}{e}} \right)}^x}}}{{\ln \frac{1}{e}}} + C = - {e^{ - x}} + C\);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} = 2\int {{3^x}} dx - \frac{1}{3}\int {{7^x}} dx = \frac{{{{2.3}^x}}}{{\ln 3}} - \frac{{{7^x}}}{{3\ln 7}} + C\).
Giải Mục 3 Trang 8,9,10 SGK Toán 12 Tập 2 - Kết Nối Tri Thức: Tổng Quan và Phương Pháp Giải
Mục 3 trong SGK Toán 12 tập 2 - Kết Nối Tri Thức tập trung vào các kiến thức về Đường Thẳng và Mặt Phẳng trong Không Gian. Đây là một phần quan trọng, nền tảng cho việc học tập các kiến thức hình học không gian ở các lớp trên. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Nội Dung Chính của Mục 3
- Vị trí tương đối của hai đường thẳng trong không gian: Song song, cắt nhau, chéo nhau.
- Góc giữa hai đường thẳng trong không gian: Cách tính góc, ứng dụng trong giải bài tập.
- Vị trí tương đối của đường thẳng và mặt phẳng trong không gian: Nằm trong mặt phẳng, song song với mặt phẳng, cắt mặt phẳng.
- Góc giữa đường thẳng và mặt phẳng trong không gian: Cách tính góc, ứng dụng trong giải bài tập.
- Khoảng cách từ một điểm đến mặt phẳng: Công thức tính, ứng dụng trong giải bài tập.
Giải Chi Tiết Các Bài Tập Trang 8,9,10
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 3 trang 8,9,10 SGK Toán 12 tập 2 - Kết Nối Tri Thức:
Bài 1 (Trang 8)
Đề bài: (Đề bài cụ thể của bài 1)
Lời giải: (Lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng và sử dụng hình vẽ minh họa nếu cần thiết)
Bài 2 (Trang 9)
Đề bài: (Đề bài cụ thể của bài 2)
Lời giải: (Lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng và sử dụng hình vẽ minh họa nếu cần thiết)
Bài 3 (Trang 10)
Đề bài: (Đề bài cụ thể của bài 3)
Lời giải: (Lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng và sử dụng hình vẽ minh họa nếu cần thiết)
Phương Pháp Giải Bài Tập Hiệu Quả
Để giải các bài tập về đường thẳng và mặt phẳng trong không gian một cách hiệu quả, các em cần nắm vững các phương pháp sau:
- Sử dụng các định lý và tính chất: Áp dụng các định lý và tính chất đã học để chứng minh các mối quan hệ giữa các đường thẳng và mặt phẳng.
- Vẽ hình: Vẽ hình chính xác và trực quan giúp các em hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng hệ tọa độ: Sử dụng hệ tọa độ để biểu diễn các điểm, đường thẳng và mặt phẳng trong không gian, từ đó giải quyết bài toán bằng phương pháp đại số.
- Phân tích bài toán: Đọc kỹ đề bài, xác định các yếu tố đã cho và yêu cầu của bài toán.
Lưu Ý Quan Trọng
Khi giải các bài tập về hình học không gian, các em cần chú ý:
- Kiểm tra lại các điều kiện của bài toán.
- Sử dụng đúng các công thức và định lý.
- Biểu diễn kết quả một cách chính xác và rõ ràng.
Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả này, các em sẽ tự tin hơn trong việc học tập và giải bài tập Mục 3 trang 8,9,10 SGK Toán 12 tập 2 - Kết Nối Tri Thức. Chúc các em học tốt!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.