Đề bài
Cho hàm số \(y = f\left( x \right) = \left| x \right|\).a) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\) và \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\). Từ đó suy ra hàm số không có đạo hàm tại \(x = 0\).b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại \(x = 0\). (Xem Hình 1.4)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cực trị hàm số để tìm cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\). Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết
a) \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left| x \right| - 0}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{x} = 1\)
\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\left| x \right| - 0}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - x}}{x} = - 1\)
Vì \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} \ne \mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\) nên hàm số không có đạo hàm tại \(x = 0\).
b) Đồ thị hàm số \(y = f\left( x \right) = \left| x \right|\):
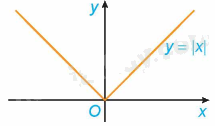
Ta có: \(y = f\left( x \right) = \left| x \right| = \left\{ \begin{array}{l} - x\;khi\;x \in \left( { - \infty ;0} \right)\\x\;\;\;khi\;x \in \left( {0; + \infty } \right)\end{array} \right.\)
Hàm số \(y = f\left( x \right) = \left| x \right|\) liên tục và xác định trên \(\left( { - \infty ; + \infty } \right)\)
Với số \(h > 0\) ta có: Với \(x \in \left( { - h;h} \right) \subset \left( { - \infty ; + \infty } \right)\) và \(x \ne 0\) thì \(y = f\left( x \right) = \left| x \right| > 0 = f\left( 0 \right)\)
Do đó, hàm số \(y = f\left( x \right) = \left| x \right|\) có cực tiểu là \(x = 0\).

