Giải bài tập 3.5 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 3.5 Trang 84 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3.5 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi hai phân xưởng được cho như sau: Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm và nhận xét về độ phân tán của tuổi thọ các linh kiện điện tử được sản xuất bởi mỗi phân xưởng.
Đề bài
Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi hai phân xưởng được cho như sau:
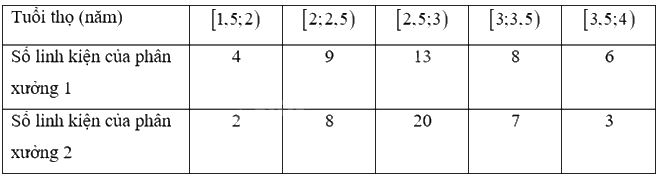
Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm và nhận xét về độ phân tán của tuổi thọ các linh kiện điện tử được sản xuất bởi mỗi phân xưởng.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Sử dụng kiến thức về ý nghĩa của độ lệch chuẩn để nhận xét: Độ lệch chuẩn dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Lời giải chi tiết
Ta có bảng số liệu với giá trị đại diện:

Phân xưởng 1: Tổng số linh kiện: \(4 + 9 + 13 + 8 + 6 = 40\)
Giá trị trung bình \(\overline {{x_1}} = \frac{{1,75.4 + 2,25.9 + 2,75.13 + 3,25.8 + 3,75.6}}{{4 + 9 + 13 + 8 + 6}} = \frac{{223}}{{80}}\)
Phương sai: \(s_1^2 = \frac{1}{{40}}\left( {1,{{75}^2}.4 + 2,{{25}^2}.9 + 2,{{75}^2}.13 + 3,{{25}^2}.8 + 3,{{75}^2}.6} \right) - {\left( {\frac{{223}}{{80}}} \right)^2} = \frac{{2271}}{{6400}}\)
Độ lệch chuẩn: \({s_1} = \sqrt {\frac{{2271}}{{6400}}} \approx 0,6\)
Phân xưởng 2: Tổng số linh kiện: \(2 + 8 + 20 + 7 + 3 = 40\)
Giá trị trung bình \(\overline {{x_2}} = \frac{{1,75.2 + 2,25.8 + 2,75.20 + 3,25.7 + 3,75.3}}{{2 + 8 + 20 + 7 + 3}} = \frac{{221}}{{80}}\)
Phương sai: \(s_2^2 = \frac{1}{{40}}\left( {1,{{75}^2}.2 + 2,{{25}^2}.8 + 2,{{75}^2}.20 + 3,{{25}^2}.7 + 3,{{75}^2}.3} \right) - {\left( {\frac{{221}}{{80}}} \right)^2} = \frac{{1399}}{{6400}}\)
Độ lệch chuẩn: \({s_2} = \sqrt {\frac{{1399}}{{6400}}} \approx 0,47\)
Vì \(0,6 > 0,47\) nên độ phân tán của phân xưởng 1 lớn hơn độ phân tán của phân xưởng 2.
Giải Bài Tập 3.5 Trang 84 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 3.5 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này thường liên quan đến việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Đề Bài:
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Lời Giải:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính đạo hàm cấp một của hàm số.
- Bước 3: Tìm các điểm dừng của hàm số.
- Bước 4: Lập bảng biến thiên.
- Bước 5: Kết luận.
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Hàm số y = x3 - 3x2 + 2 có tập xác định là D = ℝ.
y' = 3x2 - 6x
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Dựa vào bảng biến thiên, ta thấy:
Lưu Ý Quan Trọng:
Khi giải các bài toán về cực trị của hàm số, các em cần lưu ý:
- Kiểm tra tập xác định của hàm số.
- Tính đạo hàm cấp một và đạo hàm cấp hai (nếu cần).
- Tìm các điểm dừng của hàm số.
- Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến và các điểm cực trị.
Các Bài Tập Tương Tự:
Để củng cố kiến thức, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 - Kết nối tri thức và các tài liệu ôn tập khác.
Tusach.vn - Đồng Hành Cùng Các Em
Tusach.vn hy vọng rằng với hướng dẫn chi tiết này, các em sẽ hiểu rõ cách giải bài tập 3.5 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!