Lý thuyết Phương sai và độ lệch chuẩn Toán 12 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Phương sai và Độ lệch chuẩn Toán 12 Kết nối tri thức
Phương sai và độ lệch chuẩn là những khái niệm quan trọng trong chương trình Toán 12, đặc biệt trong phần Thống kê và Xác suất. Chúng giúp đo lường mức độ phân tán của một tập dữ liệu so với giá trị trung bình.
Hiểu rõ lý thuyết này là nền tảng để giải quyết các bài toán thực tế và chuẩn bị cho kỳ thi THPT Quốc gia. Tusach.vn cung cấp tài liệu học tập đầy đủ và dễ hiểu về chủ đề này.
1. Phương sai và độ lệch chuẩn
1. Phương sai và độ lệch chuẩn
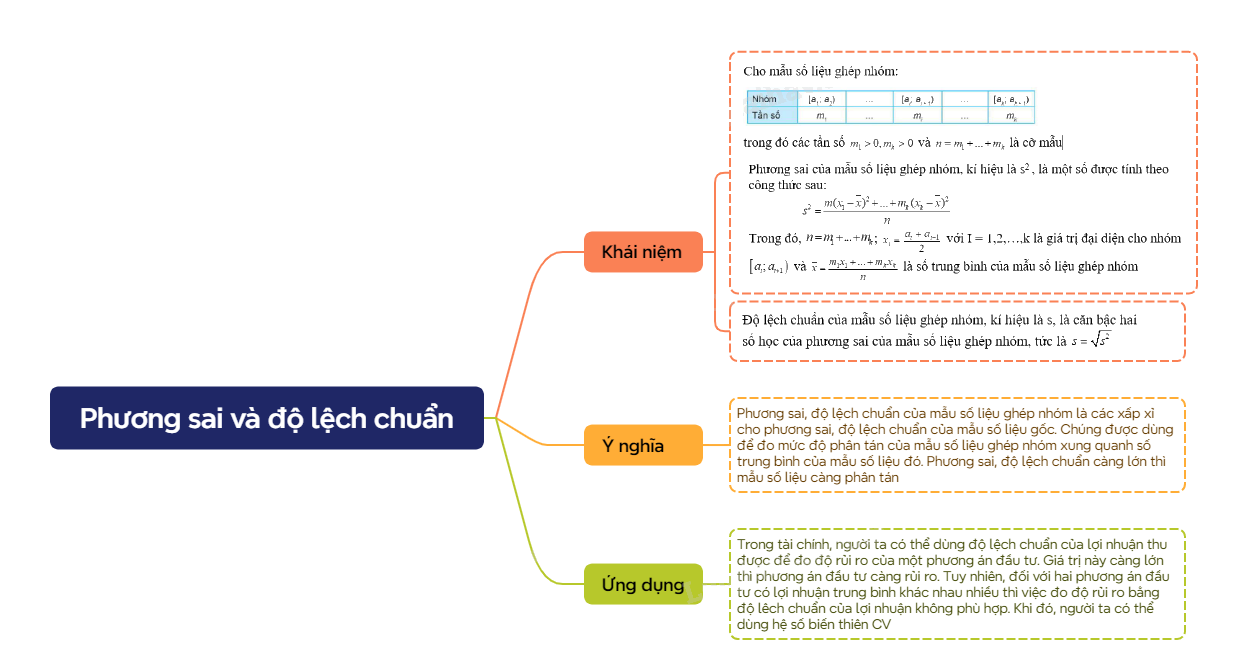
Cho mẫu số liệu ghép nhóm:

trong đó các tần số \({m_1} > 0,{m_k} > 0\) và \(n = {m_1} + ... + {m_k}\) là cỡ mẫu
Phương sai của mẫu số liệu ghép nhóm, kí hiệu là s2 , là một số được tính theo công thức sau: \[{s^2} = \frac{{m{{({x_1} - \overline x )}^2} + ... + {m_k}{{({x_k} - \overline x )}^2}}}{n}\] Trong đó, \(n = {m_1} + ... + {m_k}\); \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) với I = 1,2,…,k là giá trị đại diện cho nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) và \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm. Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \). |
Ý nghĩa: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Phương sai, độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán
2. Sử dụng phương sai, độ lệch chuẩn đo độ rủi ro
Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?
Giải:
Chọn giá trị đại diện cho các nhóm số liệu ta có:

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:
\(\overline {{x_A}} = \frac{1}{{60}}(5.7,5 + ... + 5.27,5) = 17,5\) (triệu đồng)
\(\overline {{x_B}} = \frac{1}{{60}}(20.7,5 + ... + 20.27,5) = 17,5\) (triệu đồng)
Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau
Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:
\({s_A} = \sqrt {\frac{1}{{60}}(5.7,{5^2} + ... + 5.27,{5^2} - 17,{5^2}} = 5\)
\({s_B} = \sqrt {\frac{1}{{60}}(20.7,{5^2} + ... + 20.27,{5^2} - 17,{5^2}} \approx 8,42\)
Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn
Lý thuyết Phương sai và Độ lệch chuẩn Toán 12 Kết nối tri thức: Giải thích chi tiết
Trong chương trình Toán 12 Kết nối tri thức, kiến thức về Phương sai và Độ lệch chuẩn đóng vai trò then chốt trong việc hiểu và ứng dụng các khái niệm thống kê. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết này, bao gồm định nghĩa, công thức, tính chất và các ứng dụng thực tế.
1. Biến ngẫu nhiên và các đặc trưng số đo
Trước khi đi sâu vào Phương sai và Độ lệch chuẩn, chúng ta cần ôn lại khái niệm về biến ngẫu nhiên. Biến ngẫu nhiên là một biến có giá trị phụ thuộc vào kết quả của một thí nghiệm ngẫu nhiên. Các đặc trưng số đo quan trọng của biến ngẫu nhiên bao gồm:
- Giá trị kỳ vọng (E(X)): Giá trị trung bình của biến ngẫu nhiên.
- Phương sai (Var(X)): Đo lường mức độ phân tán của biến ngẫu nhiên so với giá trị kỳ vọng.
- Độ lệch chuẩn (σ): Căn bậc hai của phương sai, cũng đo lường mức độ phân tán nhưng có đơn vị giống với biến ngẫu nhiên.
2. Định nghĩa và Công thức tính Phương sai
Định nghĩa: Phương sai của một biến ngẫu nhiên rời rạc X, ký hiệu là Var(X), là giá trị trung bình của bình phương độ lệch của các giá trị của X so với giá trị kỳ vọng E(X).
Công thức:
- Với biến ngẫu nhiên rời rạc: Var(X) = E[(X - E(X))2] = Σ[(xi - E(X))2 * P(X = xi)]
- Với mẫu số liệu: s2 = Σ[(xi - x̄)2] / (n - 1) (trong đó x̄ là trung bình mẫu, n là kích thước mẫu)
3. Định nghĩa và Công thức tính Độ lệch chuẩn
Định nghĩa: Độ lệch chuẩn của một biến ngẫu nhiên X, ký hiệu là σ, là căn bậc hai của phương sai Var(X).
Công thức: σ = √Var(X)
4. Tính chất của Phương sai và Độ lệch chuẩn
- Var(X) ≥ 0
- Var(aX + b) = a2Var(X) (với a, b là hằng số)
- σ ≥ 0
5. Ứng dụng của Phương sai và Độ lệch chuẩn
Phương sai và Độ lệch chuẩn có nhiều ứng dụng trong thực tế, bao gồm:
- Đánh giá rủi ro trong tài chính: Đo lường mức độ biến động của giá cổ phiếu, tỷ giá hối đoái,...
- Kiểm soát chất lượng trong sản xuất: Đánh giá mức độ đồng đều của sản phẩm.
- Nghiên cứu khoa học: Phân tích dữ liệu và đưa ra kết luận.
6. Ví dụ minh họa
Giả sử ta có một biến ngẫu nhiên X với các giá trị và xác suất như sau:
| xi | P(X = xi) |
|---|---|
| 1 | 0.2 |
| 2 | 0.3 |
| 3 | 0.5 |
Tính E(X), Var(X) và σ.
Giải:
E(X) = 1*0.2 + 2*0.3 + 3*0.5 = 2.3
Var(X) = (1-2.3)2*0.2 + (2-2.3)2*0.3 + (3-2.3)2*0.5 = 0.59
σ = √0.59 ≈ 0.768
7. Luyện tập và Bài tập
Để nắm vững kiến thức về Phương sai và Độ lệch chuẩn, bạn nên luyện tập thêm các bài tập khác. Tusach.vn cung cấp nhiều bài tập có đáp án để bạn tự kiểm tra và nâng cao kỹ năng.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về Lý thuyết Phương sai và Độ lệch chuẩn Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!