Giải bài tập 5.8 trang 39 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 5.8 Trang 39 Toán 12 Tập 2 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 5.8 trang 39 SGK Toán 12 tập 2 Kết nối tri thức. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn cung cấp lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?
Đề bài
Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?

Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc để chứng minh: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với hai vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right) \bot \left( \beta \right) \Leftrightarrow \overrightarrow n \bot \overrightarrow {n'} \Leftrightarrow AA' + BB' + CC' = 0\)
Lời giải chi tiết
Đặt tên bốn mái của ngôi nhà và chọn hệ trục tọa độ như hình sau:
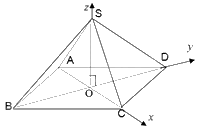
Giả sử hình vuông ABCD cạnh a và các cạnh bên bằng nhau có độ dài là b.
Vì ABCD là hình vuông, O là giao điểm của AC và BD nên \(OC = OD = OB = \frac{{a\sqrt 2 }}{2}\)
Tam giác SOC vuông tại O nên \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{2}} = \sqrt {\frac{{2{b^2} - {a^2}}}{2}} \)
Khi đó, \(O\left( {0;0;0} \right),C\left( {\frac{{a\sqrt 2 }}{2};0;0} \right),D\left( {0;\frac{{a\sqrt 2 }}{2};0} \right),B\left( {0;\frac{{ - a\sqrt 2 }}{2};0} \right),S\left( {0;0;\sqrt {\frac{{2{b^2} - {a^2}}}{2}} } \right)\)
\(\overrightarrow {SC} \left( {\frac{{a\sqrt 2 }}{2};0; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} } \right),\overrightarrow {DC} \left( {\frac{{a\sqrt 2 }}{2};\frac{{ - a\sqrt 2 }}{2};0} \right),\overrightarrow {BC} \left( {\frac{{a\sqrt 2 }}{2};\frac{{a\sqrt 2 }}{2};0} \right)\)
\(\left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {DC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }\\{ - 1}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }&{\frac{{a\sqrt 2 }}{2}}\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{\frac{{a\sqrt 2 }}{2}}&0\\1&{ - 1}\end{array}} \right|} \right)\) \( = \left( { - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{ - a\sqrt 2 }}{2}} \right)\)
\(\left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {BC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }\\1&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }&{\frac{{a\sqrt 2 }}{2}}\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{\frac{{a\sqrt 2 }}{2}}&0\\1&1\end{array}} \right|} \right) = \left( {\sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{a\sqrt 2 }}{2}} \right)\)
Mặt phẳng (SCD) nhận \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {DC} } \right] = \left( { - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{ - a\sqrt 2 }}{2}} \right)\) làm một vectơ pháp tuyến.
Mặt phẳng (SCB) nhận \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {BC} } \right] = \left( {\sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{a\sqrt 2 }}{2}} \right)\) làm một vectơ pháp tuyến.
Ta có: \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} .\sqrt {\frac{{2{b^2} - {a^2}}}{2}} + \sqrt {\frac{{2{b^2} - {a^2}}}{2}} .\sqrt {\frac{{2{b^2} - {a^2}}}{2}} + \frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^2}}}{2} \ne 0\)
Do đó, hai mặt phẳng (SCD) và (SCB) không vuông góc với nhau.
Vậy không thể thực hiện được ý tưởng trên.
Giải Bài Tập 5.8 Trang 39 Toán 12 Tập 2 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 5.8 trang 39 SGK Toán 12 tập 2 Kết nối tri thức yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Đề Bài Bài Tập 5.8
Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy:
- Xác định các khoảng đơn điệu của hàm số.
- Tìm tọa độ các điểm cực trị của hàm số.
Lời Giải Chi Tiết
Bước 1: Tính đạo hàm cấp nhất f'(x)
f'(x) = 3x2 - 6x
Bước 2: Tìm các điểm dừng (điểm mà f'(x) = 0 hoặc không xác định)
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 3: Lập bảng xét dấu f'(x)
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 4: Kết luận về khoảng đơn điệu
- Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Hàm số nghịch biến trên khoảng (0; 2).
Bước 5: Xác định tọa độ các điểm cực trị
Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên hàm số đạt cực đại tại x = 0.
f(0) = 03 - 3(0)2 + 2 = 2
Vậy, điểm cực đại là (0; 2).
Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên hàm số đạt cực tiểu tại x = 2.
f(2) = 23 - 3(2)2 + 2 = 8 - 12 + 2 = -2
Vậy, điểm cực tiểu là (2; -2).
Kết Luận
Hàm số y = x3 - 3x2 + 2:
- Đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Nghịch biến trên khoảng (0; 2).
- Điểm cực đại là (0; 2).
- Điểm cực tiểu là (2; -2).
Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 5.8 trang 39 SGK Toán 12 tập 2 Kết nối tri thức. Hãy luyện tập thêm nhiều bài tập tương tự để củng cố kiến thức nhé!
Ngoài ra, các em có thể tham khảo thêm các bài giải khác tại tusach.vn. Chúc các em học tốt!