Lý thuyết Phương trình đường thẳng Toán 12 Kết nối tri thức
Tổng quan nội dung
Lý Thuyết Phương Trình Đường Thẳng Toán 12 Kết Nối Tri Thức
Phương trình đường thẳng là một trong những kiến thức trọng tâm của chương trình Toán 12 Kết Nối Tri Thức. Việc nắm vững lý thuyết và các dạng bài tập liên quan là vô cùng quan trọng để đạt kết quả cao trong các kỳ thi. Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu về lý thuyết phương trình đường thẳng, cùng với các ví dụ minh họa chi tiết.
Chúng ta sẽ cùng tìm hiểu về các phương trình đường thẳng khác nhau, cách xác định các yếu tố của đường thẳng và ứng dụng của chúng trong giải toán.
1. Phương trình đường thẳng a) Vecto chỉ phương của đường thẳng
1. Phương trình đường thẳng
a) Vecto chỉ phương của đường thẳng
| Vecto \(\overrightarrow u \ne \overrightarrow 0 \) được gọi là vecto chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \). |
b) Phương trình tham số của đường thẳng
Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\). Hệ phương trình: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) được gọi là phương trình tham số của đường thẳng \(\Delta \) (t là tham số, \(t \in R\)). |
c) Phương trình chính tắc của đường thẳng
Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) với a, b, c là các số khác 0. Hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \). |
d) Lập phương trình đường thẳng đi qua hai điểm
Trong không gian Oxyz, cho hai điểm phân biệt \({A_1}({x_1};{y_1};{z_1})\) và \({A_2}({x_2};{y_2};{z_2})\). Đường thẳng \({A_1}{A_2}\) có vecto chỉ phương \(\overrightarrow {{A_1}{A_2}} = ({x_2} - {x_1};{y_2} - {y_1};{z_2} - {z_1})\)
|
2. Hai đường thẳng vuông góc
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) tương ứng có vecto chỉ phương \(\overrightarrow {{u_1}} ({x_1};{y_1};{z_1})\), \(\overrightarrow {{u_2}} ({x_2};{y_2};{z_2})\). Khi đó: \({\Delta _1} \bot {\Delta _2} \Leftrightarrow \overrightarrow {{u_1}} \cdot \overrightarrow {{u_2}} = 0 \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2} = 0\). |
3. Vị trí tương đối giữa hai đường thẳng
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}({x_1};{y_1};{z_1})\), \({A_2}({x_2};{y_2};{z_2})\) và tương ứng có vecto chỉ phương \(\overrightarrow {{u_1}} ({x_1};{y_1};{z_1})\), \(\overrightarrow {{u_2}} ({x_2};{y_2};{z_2})\). Khi đó:
|
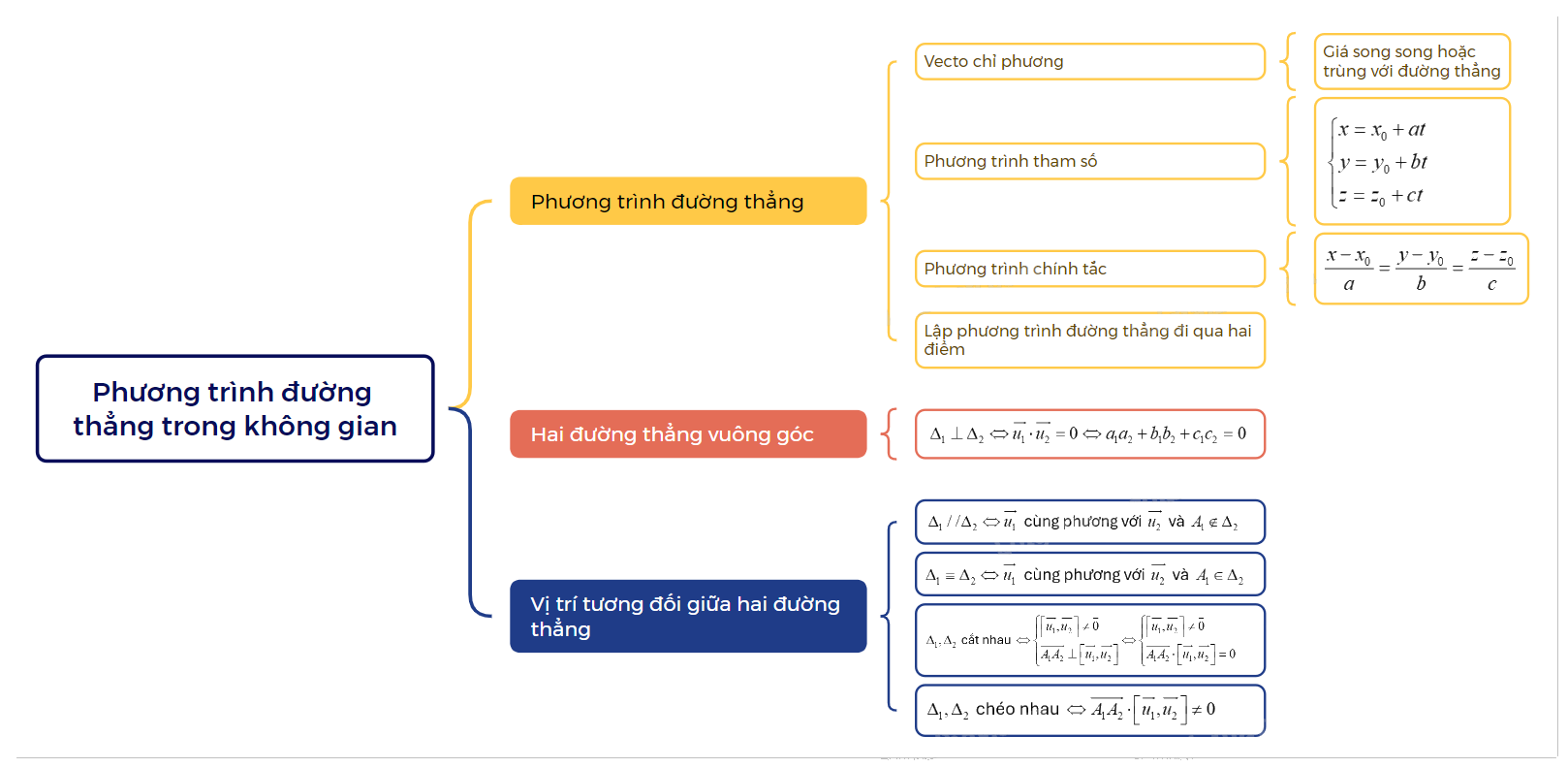
Lý Thuyết Phương Trình Đường Thẳng Toán 12 Kết Nối Tri Thức: Tổng Quan
Trong chương trình Toán 12 Kết Nối Tri Thức, phương trình đường thẳng đóng vai trò then chốt trong việc giải quyết các bài toán về hình học giải tích. Hiểu rõ các khái niệm và công thức liên quan đến phương trình đường thẳng là nền tảng để tiếp cận các chủ đề phức tạp hơn như đường thẳng và mặt phẳng trong không gian.
1. Các Dạng Phương Trình Đường Thẳng
Có ba dạng phương trình đường thẳng phổ biến:
- Phương trình tổng quát: ax + by + c = 0 (với a, b không đồng thời bằng 0)
- Phương trình tham số:
- x = x0 + at
- y = y0 + bt
- Phương trình chính tắc: (x - x0)/a = (y - y0)/b
2. Vectơ Chỉ Phương và Vectơ Pháp Tuyến
Vectơ chỉ phương của đường thẳng là một vectơ song song với đường thẳng đó. Nếu (a, b) là vectơ chỉ phương của đường thẳng ax + by + c = 0 thì (b, -a) là một vectơ pháp tuyến của đường thẳng.
3. Điều Kiện Song Song và Vuông Góc của Hai Đường Thẳng
Cho hai đường thẳng:
- d1: a1x + b1y + c1 = 0
- d2: a2x + b2y + c2 = 0
d1 song song với d2 khi và chỉ khi: a1/a2 = b1/b2 và c1/c2 ≠ a1/a2
d1 vuông góc với d2 khi và chỉ khi: a1a2 + b1b2 = 0
4. Khoảng Cách Từ Một Điểm Đến Một Đường Thẳng
Khoảng cách d từ điểm M(x0, y0) đến đường thẳng Δ: ax + by + c = 0 được tính theo công thức:
d = |ax0 + by0 + c| / √(a2 + b2)
5. Các Dạng Bài Tập Thường Gặp
Một số dạng bài tập thường gặp liên quan đến phương trình đường thẳng:
- Tìm phương trình đường thẳng đi qua hai điểm: Sử dụng công thức tính vectơ chỉ phương và phương trình tham số.
- Tìm phương trình đường thẳng đi qua một điểm và song song/vuông góc với một đường thẳng cho trước: Sử dụng điều kiện song song/vuông góc và phương trình điểm - dốc.
- Tìm giao điểm của hai đường thẳng: Giải hệ phương trình hai ẩn.
- Tính khoảng cách từ một điểm đến một đường thẳng: Sử dụng công thức tính khoảng cách.
6. Ví Dụ Minh Họa
Ví dụ 1: Tìm phương trình đường thẳng đi qua điểm A(1, 2) và song song với đường thẳng 2x - y + 3 = 0.
Giải: Vì đường thẳng cần tìm song song với 2x - y + 3 = 0 nên nó có dạng 2x - y + c = 0. Thay tọa độ điểm A(1, 2) vào phương trình, ta được: 2(1) - 2 + c = 0 => c = 0. Vậy phương trình đường thẳng cần tìm là 2x - y = 0.
7. Luyện Tập và Ôn Tập
Để nắm vững kiến thức về phương trình đường thẳng, bạn nên luyện tập thường xuyên các bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập và các trang web học trực tuyến. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn.
Chúc bạn học tốt môn Toán 12!