Lý Thuyết Giá Trị Lớn Nhất, Nhỏ Nhất Hàm Số Toán 12 - Kết Nối Tri Thức

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức

Đây là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 12, giúp học sinh nắm vững kiến thức về cực trị hàm số và ứng dụng vào giải quyết các bài toán thực tế.

Tusach.vn cung cấp tài liệu học tập đầy đủ, chi tiết, giúp bạn hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan đến giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

1. Định nghĩa Khái niệm GTLN, GTNN của hàm số

1. Định nghĩa

Khái niệm GTLN, GTNN của hàm số

Cho hàm số y = f(x) xác định trên tập D.

- Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) $ \le $ M với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = M.

Kí hiệu M = $\mathop {\max }\limits_{x \in D} f(x)$ hoặc M = $\underset{D}{\mathop{\max }}\,f(x)$

- Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) $ \ge $ m với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = m.

Kí hiệu m = $\mathop {\min }\limits_{x \in D} f(x)$ hoặc m = $\mathop {\min }\limits_D f(x)$

Ví dụ: Tìm GTLN, GTNN của hàm số $y = f(x) = \sqrt {1 - {x^2}} $

Tập xác định của hàm số là $\left[ { - 1;1} \right]$

Ta có:

$f(x) = \sqrt {1 - {x^2}} $ $ \ge $ 0; dấu bằng xảy ra khi $1 - {x^2} = 0$, tức x = -1 hoặc x = 1.

Do đó $\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f( - 1) = f(1) = 0$

$f(x) = \sqrt {1 - {x^2}} $ $ \le 1$; dấu bằng xảy ra khi $1 - {x^2} = 1$, tức x = 0.

Do đó $\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f(0) = 1$

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Giả sử y = f(x) là hàm số liên tục trên $\left[ {a;b} \right]$ và có đạo hàm trên (a;b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn $\left[ {a;b} \right]$ mà đạo hàm f’(x) = 0.

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn $\left[ {a;b} \right]$:

Tìm các điểm ${x_1},{x_2},...,{x_n} \in (a;b)$, tại đó f’(x) = 0 hoặc không tồn tại
Tính $f({x_1}),f({x_2}),...,f({x_n}),f(a)$ và $f(b)$
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

M = $\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)$; m = $\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)$

Ví dụ: Tìm GTLN và GTNN của hàm số $y = {x^4} - 4{x^2} + 3$ trên đoạn $\left[ {0;4} \right]$

Ta có: $y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0$ hoặc $x = \sqrt 2 $ (vì $x \in \left[ {0;4} \right]$)

y(0) = 3; y(4) = 195; y($\sqrt 2 $) = -1

Do đó: $\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195$; $\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) = - 1$

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức 1

Lý Thuyết Giá Trị Lớn Nhất và Giá Trị Nhỏ Nhất của Hàm Số Toán 12 - Kết Nối Tri Thức

Chủ đề giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số là một phần quan trọng trong chương trình Toán 12, đặc biệt là chương trình Kết nối tri thức. Nó không chỉ là kiến thức nền tảng cho các bài toán về cực trị hàm số mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác của toán học và khoa học kỹ thuật.

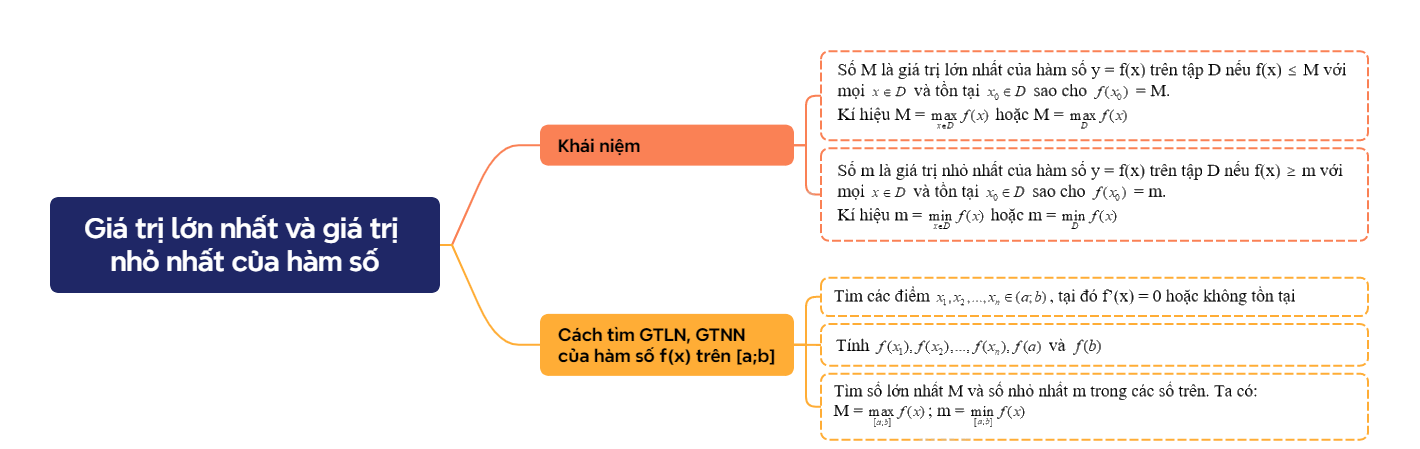
1. Khái niệm cơ bản

Giá trị lớn nhất của hàm số f(x) trên một khoảng (hoặc tập hợp) D là giá trị M sao cho f(x) ≤ M với mọi x thuộc D và tồn tại x₀ thuộc D sao cho f(x₀) = M.

Giá trị nhỏ nhất của hàm số f(x) trên một khoảng (hoặc tập hợp) D là giá trị m sao cho f(x) ≥ m với mọi x thuộc D và tồn tại x₀ thuộc D sao cho f(x₀) = m.

2. Điều kiện để hàm số đạt GTLN, GTNN trên một khoảng kín [a, b]

Nếu hàm số f(x) liên tục trên [a, b] thì:

f(x) đạt GTLN và GTNN trên [a, b]
GTLN và GTNN có thể đạt tại các điểm:
- Các điểm mà f'(x) = 0 (điểm dừng)
- Các điểm mà f'(x) không tồn tại
- Các mút của khoảng [a, b]

3. Phương pháp tìm GTLN, GTNN của hàm số

Tìm tập xác định của hàm số.
Tính đạo hàm f'(x).
Tìm các điểm dừng (f'(x) = 0) và các điểm mà f'(x) không tồn tại.
Tính giá trị của hàm số tại các điểm dừng, điểm mà đạo hàm không tồn tại và các mút của khoảng (nếu có).
So sánh các giá trị tìm được để xác định GTLN và GTNN.

4. Ví dụ minh họa

Ví dụ 1: Tìm GTLN và GTNN của hàm số f(x) = x³ - 3x² + 2 trên đoạn [-1, 3].

Giải:

f'(x) = 3x² - 6x
f'(x) = 0 ⇔ 3x² - 6x = 0 ⇔ x = 0 hoặc x = 2
f(-1) = 0
f(0) = 2
f(2) = -2
f(3) = 2

Vậy GTLN của f(x) trên [-1, 3] là 2, đạt tại x = 0 và x = 3. GTNN của f(x) trên [-1, 3] là -2, đạt tại x = 2.

5. Lưu ý quan trọng

Khi tìm GTLN và GTNN của hàm số, cần chú ý đến tập xác định của hàm số và kiểm tra xem hàm số có liên tục trên khoảng đang xét hay không. Ngoài ra, cần xem xét kỹ các điểm mà đạo hàm không tồn tại, vì đây cũng có thể là điểm đạt GTLN hoặc GTNN.

6. Bài tập áp dụng

Để củng cố kiến thức, bạn có thể thực hành giải các bài tập sau:

Tìm GTLN và GTNN của hàm số f(x) = x² - 4x + 3 trên đoạn [0, 4].
Tìm GTLN và GTNN của hàm số f(x) = sinx trên khoảng [0, π].

Tusach.vn hy vọng với những kiến thức và ví dụ trên, bạn sẽ nắm vững lý thuyết về giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức

Lý Thuyết Giá Trị Lớn Nhất và Giá Trị Nhỏ Nhất của Hàm Số Toán 12 - Kết Nối Tri Thức

1. Khái niệm cơ bản

2. Điều kiện để hàm số đạt GTLN, GTNN trên một khoảng kín [a, b]

3. Phương pháp tìm GTLN, GTNN của hàm số

4. Ví dụ minh họa

5. Lưu ý quan trọng

6. Bài tập áp dụng

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN