Giải bài tập 3.17 trang 86 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 3.17 Trang 86 Toán 12 Tập 1 - Kết Nối Tri Thức
Bài tập 3.17 trang 86 SGK Toán 12 tập 1 Kết nối tri thức là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau: Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả số đo của An và Bình. Từ đó kết luận xem vôn kết của bạn nào cho kết quả ổn định hơn.
Đề bài
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau: 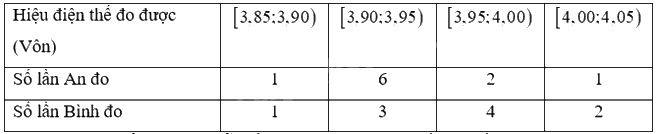
Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả số đo của An và Bình. Từ đó kết luận xem vôn kết của bạn nào cho kết quả ổn định hơn.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
+ Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \).
+ Sử dụng kiến thức về nghĩa của độ lệch chuẩn để đưa ra kết luận: Nếu độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Lời giải chi tiết
Mẫu số liệu với giá trị đại diện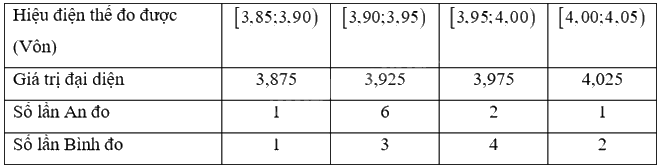
Kết quả đo của An:
Giá trị trung bình: \(\overline {{x_1}} = \frac{1}{{10}}\left( {3,875.1 + 3,925.6 + 3,975.2 + 4,025.1} \right) = 3,94\)
Phương sai của mẫu số liệu:
\({s_1}^2 = \frac{1}{{10}}\left( {3,{{875}^2}.1 + 3,{{925}^2}.6 + 3,{{975}^2}.2 + 4,{{025}^2}.1} \right) - 3,{94^2} = 0,001525\)
Độ lệch chuẩn của mẫu số liệu: \({s_1} = \sqrt {0,001525} \approx 0,039\)
Kết quả đo của Bình:
Giá trị trung bình: \(\overline {{x_1}} = \frac{1}{{10}}\left( {3,875.1 + 3,925.3 + 3,975.4 + 4,025.4} \right) = 3,96\)
Phương sai của mẫu số liệu:
\({s_2}^2 = \frac{1}{{10}}\left( {3,{{875}^2}.1 + 3,{{925}^2}.3 + 3,{{975}^2}.4 + 4,{{025}^2}.2} \right) - 3,{96^2} = 0,002025\)
Độ lệch chuẩn của mẫu số liệu: \({s_2} = \sqrt {0,002025} \approx 0,045\)
Vì \({s_2} > {s_1}\) nên Vôn kế của bạn An cho kết quả ổn định hơn.
Giải Bài Tập 3.17 Trang 86 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 3.17 trang 86 SGK Toán 12 tập 1 Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
- Định nghĩa đạo hàm
- Các quy tắc tính đạo hàm (quy tắc tổng, hiệu, tích, thương, hàm hợp)
- Đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit)
- Ứng dụng của đạo hàm để giải các bài toán thực tế
Nội Dung Bài Tập 3.17
Bài tập 3.17 thường yêu cầu học sinh thực hiện các thao tác sau:
- Tính đạo hàm của hàm số cho trước.
- Tìm điểm cực trị của hàm số.
- Khảo sát sự biến thiên của hàm số.
- Giải các bài toán liên quan đến ứng dụng của đạo hàm (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước).
Lời Giải Chi Tiết Bài Tập 3.17
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập 3.17, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu chúng ta tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1.
Bước 1: Tính đạo hàm f'(x)
Áp dụng quy tắc tính đạo hàm của hàm đa thức, ta có:
f'(x) = 3x2 - 6x + 2
Bước 2: Tìm điểm cực trị
Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x + 2 = 0
Sử dụng công thức nghiệm của phương trình bậc hai, ta tìm được hai nghiệm:
x1 = (6 + √12) / 6 = 1 + √3/3
x2 = (6 - √12) / 6 = 1 - √3/3
Bước 3: Xác định loại điểm cực trị
Ta xét dấu của đạo hàm bậc hai f''(x) tại các điểm cực trị:
f''(x) = 6x - 6
f''(x1) = 6(1 + √3/3) - 6 = 2√3 > 0, do đó x1 là điểm cực tiểu.
f''(x2) = 6(1 - √3/3) - 6 = -2√3 < 0, do đó x2 là điểm cực đại.
Lưu Ý Khi Giải Bài Tập
Khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:
- Nắm vững các quy tắc tính đạo hàm.
- Kiểm tra kỹ các bước tính toán để tránh sai sót.
- Vận dụng linh hoạt các kiến thức đã học để giải quyết các bài toán khác nhau.
- Thực hành giải nhiều bài tập để rèn luyện kỹ năng.
Tổng Kết
Bài tập 3.17 trang 86 SGK Toán 12 tập 1 Kết nối tri thức là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ bạn!