Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 1.39 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức
SGK Toán 12 - Kết nối tri thức
Giải Toán 12 tập 1 - Kết nối tri thức
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Bài tập cuối chương 1

Giải bài tập 1.39 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức

Giải Bài Tập 1.39 Trang 43 Toán 12 Tập 1 - Kết Nối Tri Thức

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài tập 1.39 trang 43 một cách dễ hiểu nhất.

Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

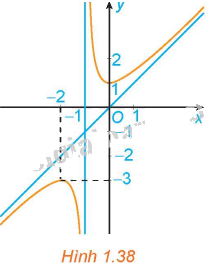
Đồ thị trong Hình 1.38 là đồ thị của hàm số: A. \(y = x - \frac{1}{{x + 1}}\). B. \(y = \frac{{2x + 1}}{{x + 1}}\). C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\). D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).

Đề bài

Đồ thị trong Hình 1.38 là đồ thị của hàm số:

Giải bài tập 1.39 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức 1 A. \(y = x - \frac{1}{{x + 1}}\).B. \(y = \frac{{2x + 1}}{{x + 1}}\).C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\).D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).

Phương pháp giải - Xem chi tiếtGiải bài tập 1.39 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức 2

Sử dụng kiến thức về điểm thuộc đồ thị hàm số, dạng của đồ thị hàm số, tiệm cận của đồ thị hàm số để tìm đồ thị hàm số đúng.

Lời giải chi tiết

Đồ thị hàm số trong hình 1.38 có dạng: \(y = \frac{{a{x^2} + bx + c}}{{px + q}}\left( {a \ne 0,p \ne 0} \right)\) và đa thức tử không chia hết cho đa thức mẫu. Do đó, loại đáp án B.

Đồ thị hàm số trong hình 1.38 đi qua điểm \[\left( { - 2; - 3} \right)\]. Do đó, loại đáp án C.

Đồ thị hàm số trong hình 1.38 đi qua điểm (0; 1). Do đó, loại đáp án A.

Hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}} = x + \frac{1}{{x + 1}}\) có:

+ \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{{x^2} + x + 1}}{{x + 1}} = + \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + x + 1}}{{x + 1}} = - \infty \) nên đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị hàm số.

+ \(\mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 1}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x + 1}} = 0\) nên đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số.

Chọn D

Giải Bài Tập 1.39 Trang 43 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết

Bài tập 1.39 trang 43 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu chúng ta vận dụng kiến thức về đạo hàm của hàm số để giải quyết. Dưới đây là lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp và áp dụng vào các bài tập tương tự.

Đề Bài:

Cho hàm số f(x) = x3 - 3x2 + 2. Tìm đạo hàm f'(x) và xác định các điểm cực trị của hàm số.

Lời Giải:

  1. Tính đạo hàm f'(x):

    2. Sử dụng quy tắc đạo hàm của tổng và lũy thừa, ta có:

    f'(x) = 3x2 - 6x

  2. Tìm điểm cực trị:

    3. Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:

    3x2 - 6x = 0

    3x(x - 2) = 0

    Vậy, x = 0 hoặc x = 2

  3. Xác định loại điểm cực trị:

    4. Ta xét dấu của f'(x) trên các khoảng:

    • Khoảng (-∞, 0): Chọn x = -1, f'(-1) = 3(-1)2 - 6(-1) = 9 > 0, hàm số đồng biến.
    • Khoảng (0, 2): Chọn x = 1, f'(1) = 3(1)2 - 6(1) = -3 < 0, hàm số nghịch biến.
    • Khoảng (2, +∞): Chọn x = 3, f'(3) = 3(3)2 - 6(3) = 9 > 0, hàm số đồng biến.

    Vậy:

    • Tại x = 0, hàm số đạt cực đại. Giá trị cực đại là f(0) = 03 - 3(0)2 + 2 = 2.
    • Tại x = 2, hàm số đạt cực tiểu. Giá trị cực tiểu là f(2) = 23 - 3(2)2 + 2 = 0.

Kết Luận:

Hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại điểm (0, 2) và đạt cực tiểu tại điểm (2, 0).

Lưu Ý Quan Trọng:

Khi giải các bài tập về đạo hàm và cực trị, bạn cần nắm vững các quy tắc đạo hàm cơ bản và phương pháp xét dấu đạo hàm để xác định đúng loại điểm cực trị.

Các Bài Tập Tương Tự:

Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 Kết nối tri thức và các tài liệu luyện thi THPT Quốc gia.

Tusach.vn - Đồng Hành Cùng Bạn Trên Con Đường Học Tập

Tusach.vn luôn cập nhật lời giải các bài tập mới nhất và cung cấp nhiều tài liệu học tập hữu ích khác. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập của bạn!

Bài TậpTrang
Bài 1.3843
Bài 1.4043

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN