Giải mục 1 trang 54,55,56 SGK Toán 12 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 54,55,56 SGK Toán 12 tập 2 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 54, 55, 56 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Chúng tôi hiểu rằng việc tự học và làm bài tập có thể gặp nhiều khó khăn. Vì vậy, tusach.vn luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ các em học tập hiệu quả.
PHƯƠNG TRÌNH MẶT CẦU
LT2
Trả lời câu hỏi Luyện tập 2 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:
a) Tâm là gốc tọa độ, bán kính \(R = 1\).
b) Đường kính AB, với \(A\left( {1; - 1;2} \right),B\left( {2; - 3; - 1} \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để viết phương trình mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Lời giải chi tiết:
a) Mặt cầu (S) có tâm \(O\left( {0;0;0} \right)\), bán kính \(R = 1\) nên có phương trình là: \({x^2} + {y^2} + {z^2} = 1\)
b) Đoạn thẳng AB có trung điểm là \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\).
Mặt cầu (S) có bán kính \(R = \frac{1}{2}AB = \frac{1}{2}\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( { - 3 + 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \frac{{\sqrt {14} }}{2}\) và tâm \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\). Do đó, (S): \({\left( {x - \frac{3}{2}} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{7}{2}\)
LT1
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \({\left( {x + 2} \right)^2} + {y^2} + {\left( {z + \frac{1}{2}} \right)^2} = \frac{9}{4}\).
a) Xác định tâm và bán kính của (S).
b) Hỏi điểm \(M\left( {2;0;1} \right)\) nằm trong, nằm ngoài hay thuộc mặt cầu (S)?
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để xác định tâm và bán kính của mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Sử dụng kiến thức về phương trình mặt cầu để xác định vị trí của điểm so với mặt cầu: Cho mặt cầu (S) tâm I, bán kính R và điểm M bất kì trong không gian:
+ Nếu \(IM = R\) thì M nằm trên mặt cầu (S) tâm I.
+ Nếu \(IM > R\) thì M nằm ngoài mặt cầu (S) tâm I.
+ Nếu \(IM < R\) thì M nằm trong mặt cầu (S) tâm I.
Lời giải chi tiết:
a) Ta viết lại phương trình mặt cầu (S) dưới dạng:
\({\left[ {x - \left( { - 2} \right)} \right]^2} + {\left( {y - 0} \right)^2} + {\left[ {z - \left( { - \frac{1}{2}} \right)} \right]^2} = {\left( {\frac{3}{2}} \right)^2}\)
Do đó, mặt cầu (S) có tâm \(I\left( { - 2;0;\frac{{ - 1}}{2}} \right)\) và bán kính \(R = \frac{3}{2}\).
b) Ta có: \(MI = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {0 - 0} \right)}^2} + {{\left( {\frac{{ - 1}}{2} - 1} \right)}^2}} = \frac{{\sqrt {73} }}{2} > \frac{3}{2} = R\) nên điểm \(M\left( {2;0;1} \right)\) nằm ngoài mặt cầu (S).
LT3
Trả lời câu hỏi Luyện tập 3 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho (S) là tập hợp các điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) có tọa độ thỏa mãn phương trình: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\). Chứng minh rằng (S) là một mặt cầu. Xác định tâm và bán kính của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để chứng minh: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;b;c} \right),\) bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
Lời giải chi tiết:
Ta có: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\)
\( \Leftrightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) + {z^2} = 25\)\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = {5^2}\)
Do đó, (S) là mặt cầu có tâm \(I\left( {2; - 3;0} \right)\) và bán kính \(R = 5\).
LT4
Trả lời câu hỏi Luyện tập 4 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình:
\({x^2} + {y^2} + {z^2} + 4x - 5y + 6z + \frac{{25}}{4} = 0\).
Xác định tâm, tính bán kính của (S).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để tính: Với a, b, c, d là các hằng số, phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có thể viết lại thành \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {a^2} + {b^2} + {c^2} - d\) và là phương trình của một mặt cầu (S) khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\). Khi đó, (S) có tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Lời giải chi tiết:
Phương trình mặt cầu (S) đã cho tương ứng với \(a = - 2;b = \frac{5}{2};c = - 3,d = \frac{{25}}{4}\)
Nên mặt cầu (S) có tâm \(I\left( { - 2;\frac{5}{2}; - 3} \right)\), bán kính \(R = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( { - 3} \right)}^2} - \frac{{25}}{4}} = \sqrt {13} \)
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Kết nối tri thức
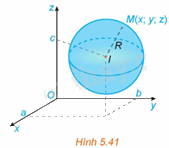
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?
Phương pháp giải:
Sử dụng kiến thức về mặt cầu tâm để tìm điều kiện:
+ Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
+ Mỗi đường thẳng đi qua tâm mặt cầu đều cắt mặt cầu tại hai điểm phân biệt, đoạn thẳng nối hai điểm đó được gọi là đường kính mặt cầu. Mỗi đường kính của mặt cầu đều có trung điểm là tâm mặt cầu và có độ dài bằng hai lần bán kính mặt cầu.
Lời giải chi tiết:
Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
Do đó, điểm thuộc mặt cầu (S) khi và chỉ khi .
- HĐ1
- LT1
- LT2
- LT3
- LT4
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?

Phương pháp giải:
Sử dụng kiến thức về mặt cầu tâm để tìm điều kiện:
+ Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
+ Mỗi đường thẳng đi qua tâm mặt cầu đều cắt mặt cầu tại hai điểm phân biệt, đoạn thẳng nối hai điểm đó được gọi là đường kính mặt cầu. Mỗi đường kính của mặt cầu đều có trung điểm là tâm mặt cầu và có độ dài bằng hai lần bán kính mặt cầu.
Lời giải chi tiết:
Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
Do đó, điểm thuộc mặt cầu (S) khi và chỉ khi .
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \({\left( {x + 2} \right)^2} + {y^2} + {\left( {z + \frac{1}{2}} \right)^2} = \frac{9}{4}\).
a) Xác định tâm và bán kính của (S).
b) Hỏi điểm \(M\left( {2;0;1} \right)\) nằm trong, nằm ngoài hay thuộc mặt cầu (S)?
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để xác định tâm và bán kính của mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Sử dụng kiến thức về phương trình mặt cầu để xác định vị trí của điểm so với mặt cầu: Cho mặt cầu (S) tâm I, bán kính R và điểm M bất kì trong không gian:
+ Nếu \(IM = R\) thì M nằm trên mặt cầu (S) tâm I.
+ Nếu \(IM > R\) thì M nằm ngoài mặt cầu (S) tâm I.
+ Nếu \(IM < R\) thì M nằm trong mặt cầu (S) tâm I.
Lời giải chi tiết:
a) Ta viết lại phương trình mặt cầu (S) dưới dạng:
\({\left[ {x - \left( { - 2} \right)} \right]^2} + {\left( {y - 0} \right)^2} + {\left[ {z - \left( { - \frac{1}{2}} \right)} \right]^2} = {\left( {\frac{3}{2}} \right)^2}\)
Do đó, mặt cầu (S) có tâm \(I\left( { - 2;0;\frac{{ - 1}}{2}} \right)\) và bán kính \(R = \frac{3}{2}\).
b) Ta có: \(MI = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {0 - 0} \right)}^2} + {{\left( {\frac{{ - 1}}{2} - 1} \right)}^2}} = \frac{{\sqrt {73} }}{2} > \frac{3}{2} = R\) nên điểm \(M\left( {2;0;1} \right)\) nằm ngoài mặt cầu (S).
Trả lời câu hỏi Luyện tập 2 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:
a) Tâm là gốc tọa độ, bán kính \(R = 1\).
b) Đường kính AB, với \(A\left( {1; - 1;2} \right),B\left( {2; - 3; - 1} \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để viết phương trình mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Lời giải chi tiết:
a) Mặt cầu (S) có tâm \(O\left( {0;0;0} \right)\), bán kính \(R = 1\) nên có phương trình là: \({x^2} + {y^2} + {z^2} = 1\)
b) Đoạn thẳng AB có trung điểm là \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\).
Mặt cầu (S) có bán kính \(R = \frac{1}{2}AB = \frac{1}{2}\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( { - 3 + 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \frac{{\sqrt {14} }}{2}\) và tâm \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\). Do đó, (S): \({\left( {x - \frac{3}{2}} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{7}{2}\)
Trả lời câu hỏi Luyện tập 3 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho (S) là tập hợp các điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) có tọa độ thỏa mãn phương trình: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\). Chứng minh rằng (S) là một mặt cầu. Xác định tâm và bán kính của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để chứng minh: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;b;c} \right),\) bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
Lời giải chi tiết:
Ta có: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\)
\( \Leftrightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) + {z^2} = 25\)\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = {5^2}\)
Do đó, (S) là mặt cầu có tâm \(I\left( {2; - 3;0} \right)\) và bán kính \(R = 5\).
Trả lời câu hỏi Luyện tập 4 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình:
\({x^2} + {y^2} + {z^2} + 4x - 5y + 6z + \frac{{25}}{4} = 0\).
Xác định tâm, tính bán kính của (S).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để tính: Với a, b, c, d là các hằng số, phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có thể viết lại thành \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {a^2} + {b^2} + {c^2} - d\) và là phương trình của một mặt cầu (S) khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\). Khi đó, (S) có tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Lời giải chi tiết:
Phương trình mặt cầu (S) đã cho tương ứng với \(a = - 2;b = \frac{5}{2};c = - 3,d = \frac{{25}}{4}\)
Nên mặt cầu (S) có tâm \(I\left( { - 2;\frac{5}{2}; - 3} \right)\), bán kính \(R = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( { - 3} \right)}^2} - \frac{{25}}{4}} = \sqrt {13} \)
Giải mục 1 trang 54,55,56 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 54, 55, 56 SGK Toán 12 tập 2 Kết nối tri thức tập trung vào việc ôn tập chương 3: Đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, đòi hỏi học sinh phải nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm để giải quyết các bài toán thực tế.
Nội dung chính của Mục 1
- Ôn tập lý thuyết: Các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm, ứng dụng của đạo hàm trong việc tìm cực trị, điểm uốn, và khảo sát hàm số.
- Bài tập vận dụng: Các bài tập áp dụng các kiến thức đã học để giải quyết các bài toán cụ thể, giúp học sinh rèn luyện kỹ năng và hiểu sâu hơn về đạo hàm.
- Bài tập trắc nghiệm: Các bài tập trắc nghiệm giúp học sinh kiểm tra kiến thức và đánh giá khả năng tự giải quyết vấn đề.
Giải chi tiết các bài tập trong Mục 1
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 54, 55, 56 SGK Toán 12 tập 2 Kết nối tri thức:
Bài 1: Tính đạo hàm của các hàm số sau
a) y = x3 - 2x2 + 5x - 1
Lời giải: y' = 3x2 - 4x + 5
b) y = (x2 + 1)(x - 2)
Lời giải: y' = 2x(x - 2) + (x2 + 1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Bài 2: Tìm đạo hàm của hàm số y = sin(2x)
Lời giải: y' = cos(2x) * 2 = 2cos(2x)
Bài 3: Tìm đạo hàm của hàm số y = ex + ln(x)
Lời giải: y' = ex + 1/x
Bài 4: Tìm đạo hàm cấp hai của hàm số y = x4
Lời giải:
- y' = 4x3
- y'' = 12x2
Mẹo học tập hiệu quả
Để học tốt môn Toán 12, đặc biệt là phần đạo hàm, các em cần:
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên các bài tập để rèn luyện kỹ năng.
- Hiểu rõ bản chất của các khái niệm và ứng dụng của đạo hàm.
- Sử dụng các tài liệu tham khảo và công cụ hỗ trợ học tập.
Kết luận
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 54, 55, 56 SGK Toán 12 tập 2 Kết nối tri thức. Chúc các em học tập tốt!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.