Giải bài tập 3.7 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 3.7 Trang 84 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3.7 trang 84 SGK Toán 12 tập 1 Kết nối tri thức. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn sẽ cung cấp lời giải bài tập này một cách dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Thời gian chạy tập luyện cự li 100m của hai vận động viên được cho trong bảng sau: Dựa trên độ lệch chuẩn của mẫu số liệu ghép nhóm, hãy cho biết vận động viên nào có thành tích luyện tập ổn định hơn.
Đề bài
Thời gian chạy tập luyện cự li 100m của hai vận động viên được cho trong bảng sau: 
Dựa trên độ lệch chuẩn của mẫu số liệu ghép nhóm, hãy cho biết vận động viên nào có thành tích luyện tập ổn định hơn.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
b) Sử dụng kiến thức về ý nghĩa của độ lệch chuẩn để nhận xét: Độ lệch chuẩn dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Lời giải chi tiết
Ta có bảng số liệu với giá trị đại diện: 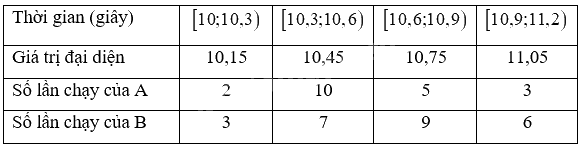
Vận động viên A:
Giá trị trung bình \(\overline {{x_A}} = \frac{{10,15.2 + 10,45.10 + 10,75.5 + 11,05.3}}{{2 + 10 + 5 + 3}} = \frac{{2117}}{{200}}\)
Phương sai: \(s_A^2 = \frac{1}{{20}}\left( {10,{{15}^2}.2 + 10,{{45}^2}.10 + 10,{{75}^2}.5 + 11,{{05}^2}.3} \right) - {\left( {\frac{{2117}}{{200}}} \right)^2} = \frac{{2691}}{{40000}}\)
Độ lệch chuẩn: \({s_A} = \sqrt {\frac{{2691}}{{40000}}} \approx 0,26\)
Vận động viên B:
Giá trị trung bình \(\overline {{x_B}} = \frac{{10,15.3 + 10,45.7 + 10,75.9 + 11,05.6}}{{3 + 7 + 9 + 6}} = \frac{{5333}}{{500}}\)
Phương sai: \(s_B^2 = \frac{1}{{25}}\left( {10,{{15}^2}.3 + 10,{{45}^2}.7 + 10,{{75}^2}.9 + 11,{{05}^2}.6} \right) - {\left( {\frac{{5333}}{{500}}} \right)^2} = \frac{{1296}}{{15625}}\)
Độ lệch chuẩn: \({s_B} = \sqrt {\frac{{1296}}{{15625}}} = 0,288\)
Vì \({s_A} < {s_B}\) nên vận động viên A có thành tích luyện tập ổn định hơn.
Giải Bài Tập 3.7 Trang 84 Toán 12 Tập 1 - Kết Nối Tri Thức: Chi Tiết và Dễ Hiểu
Bài tập 3.7 trang 84 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Đề Bài Bài Tập 3.7
Cho hàm số y = x3 - 3x2 + 2. Hãy:
- Xác định các khoảng đơn điệu của hàm số.
- Tìm tọa độ các điểm cực trị của hàm số.
Lời Giải Chi Tiết
Bước 1: Tính đạo hàm cấp nhất
y' = 3x2 - 6x
Bước 2: Tìm các điểm dừng
y' = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, các điểm dừng là x = 0 và x = 2.
Bước 3: Lập bảng xét dấu đạo hàm cấp nhất
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | ĐB | NB |
(NB: Đồng biến, ĐB: Nghịch biến)
Bước 4: Kết luận về khoảng đơn điệu
- Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Hàm số nghịch biến trên khoảng (0; 2).
Bước 5: Tìm tọa độ các điểm cực trị
Tại x = 0, y = 03 - 3(0)2 + 2 = 2. Vậy điểm cực đại là (0; 2).
Tại x = 2, y = 23 - 3(2)2 + 2 = 8 - 12 + 2 = -2. Vậy điểm cực tiểu là (2; -2).
Kết Luận
Hàm số y = x3 - 3x2 + 2:
- Đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Nghịch biến trên khoảng (0; 2).
- Điểm cực đại là (0; 2).
- Điểm cực tiểu là (2; -2).
Các Bài Tập Tương Tự
Để củng cố kiến thức về khảo sát hàm số, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 Kết nối tri thức và các tài liệu luyện tập khác. Tusach.vn sẽ tiếp tục cập nhật lời giải chi tiết cho các bài tập còn lại.
Hy vọng lời giải chi tiết bài tập 3.7 trang 84 SGK Toán 12 tập 1 Kết nối tri thức này sẽ giúp các em hiểu rõ hơn về phương pháp giải và tự tin hơn trong quá trình học tập. Chúc các em học tốt!