Giải mục 3 trang 70, 71 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 3 trang 70, 71 SGK Toán 12 tập 1 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 70, 71 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ lý thuyết và phương pháp giải các bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của các em.
Vận dụng tọa độ của vectơ trong một số bài toán có liên quan đến thực tiễn
LT5
Trả lời câu hỏi Luyện tập 5 trang 76SGK Toán 12 Kết nối tri thức
Với các giả thiết như trong Ví dụ 5, hãy xác định tọa độ của các chiếc máy bay sau 10 phút tiếp theo (tính từ thời điểm máy bay ở điểm B).
Phương pháp giải:
Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).
Lời giải chi tiết:
Gọi D(x; y; z) là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm B). Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BD} \) cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ A đến B bằng thời gian bay từ B đến D nên \(AB = BD\). Do đó, \(\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)\).
Mặt khác: \(\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)\) nên \(\left\{ \begin{array}{l}x - 940 = 140\\y - 550 = 50\\z - 8 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\;080\\y = 600\\z = 9\end{array} \right.\)
Vậy D(1 080; 600; 9). Vậy tọa độ của máy bay trong 10 phút tiếp theo là (1 080; 600; 9).
LT7
Trả lời câu hỏi Luyện tập 7 trang 72 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 7, khinh khí cầu thứ nhất hay thứ hai ở xa điểm xuất phát hơn? Giải thích vì sao.
Phương pháp giải:
Sử dụng kiến thức về tính độ dài của vectơ trong không gian: Trong không gian Oxyz, cho \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Lời giải chi tiết:
Theo Ví dụ 7 ta có, khinh khí cầu thứ nhất có tọa độ là A(2; 1; 0,5), khinh khí cầu thứ hai có tọa độ là \(B\left( { - 1; - 1,5;0,8} \right)\).
Ta có: \(OA = \sqrt {{2^2} + {1^2} + 0,{5^2}} = \frac{{\sqrt {21} }}{2}km\), \(OB = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1,5} \right)}^2} + 0,{8^2}} = \frac{{\sqrt {389} }}{{10}}km\).
Vì gốc O đặt tại điểm xuất phát và \(OA > OB\) nên khinh khí cầu thứ hai gần điểm xuất phát hơn.
LT1
Trả lời câu hỏi Luyện tập 6 trang 71SGK Toán 12 Kết nối tri thức
Trong tình huống mở đầu, hãy tính độ lớn của góc \(\alpha \).
Phương pháp giải:
Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính: Nếu \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) là hai vectơ khác \(\overrightarrow 0 \) thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{xx' + yy' + zz'}}{{\sqrt {{x^2} + {y^2} + {z^2}} .\sqrt {x{'^2} + y{'^2} + z{'^2}} }}\)
Lời giải chi tiết:
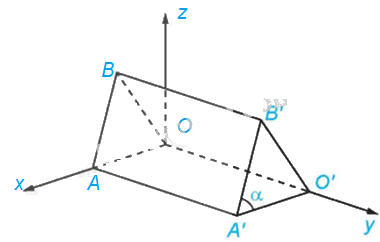
Theo Ví dụ 6 ta có: \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right);\left| {\overrightarrow {A'B'} } \right| = 60\sqrt {29} cm,O'\left( {0;450;0} \right),\)\(A'\left( {240;450;0} \right)\)
Do đó, \(\overrightarrow {A'O'} = \left( { - 240;0;0} \right) \Rightarrow \left| {\overrightarrow {A'O'} } \right| = 240cm\)
Ta có: \(\cos \left( {\overrightarrow {A'B'} ;\overrightarrow {A'O'} } \right) = \frac{{\overrightarrow {A'B'} .\overrightarrow {A'O'} }}{{\left| {\overrightarrow {A'B'} } \right|.\left| {\overrightarrow {A'O'} } \right|}} = \frac{{\left( { - 120} \right)\left( { - 240} \right) + 0.0 + 300.0}}{{60\sqrt {29} .240}} = \frac{{2\sqrt {29} }}{{29}}\)
\( \Rightarrow \widehat {B'A'O'} \approx {68^0}\). Vậy \(\alpha \approx {68^0}\)
- LT5
- LT1
- LT7
Trả lời câu hỏi Luyện tập 5 trang 76SGK Toán 12 Kết nối tri thức
Với các giả thiết như trong Ví dụ 5, hãy xác định tọa độ của các chiếc máy bay sau 10 phút tiếp theo (tính từ thời điểm máy bay ở điểm B).
Phương pháp giải:
Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).
Lời giải chi tiết:
Gọi D(x; y; z) là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm B). Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BD} \) cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ A đến B bằng thời gian bay từ B đến D nên \(AB = BD\). Do đó, \(\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)\).
Mặt khác: \(\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)\) nên \(\left\{ \begin{array}{l}x - 940 = 140\\y - 550 = 50\\z - 8 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\;080\\y = 600\\z = 9\end{array} \right.\)
Vậy D(1 080; 600; 9). Vậy tọa độ của máy bay trong 10 phút tiếp theo là (1 080; 600; 9).
Trả lời câu hỏi Luyện tập 6 trang 71SGK Toán 12 Kết nối tri thức
Trong tình huống mở đầu, hãy tính độ lớn của góc \(\alpha \).
Phương pháp giải:
Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính: Nếu \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) là hai vectơ khác \(\overrightarrow 0 \) thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{xx' + yy' + zz'}}{{\sqrt {{x^2} + {y^2} + {z^2}} .\sqrt {x{'^2} + y{'^2} + z{'^2}} }}\)
Lời giải chi tiết:
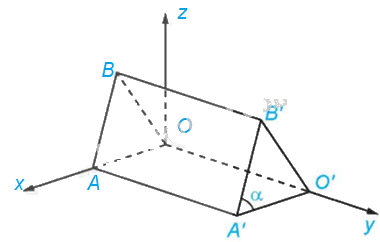
Theo Ví dụ 6 ta có: \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right);\left| {\overrightarrow {A'B'} } \right| = 60\sqrt {29} cm,O'\left( {0;450;0} \right),\)\(A'\left( {240;450;0} \right)\)
Do đó, \(\overrightarrow {A'O'} = \left( { - 240;0;0} \right) \Rightarrow \left| {\overrightarrow {A'O'} } \right| = 240cm\)
Ta có: \(\cos \left( {\overrightarrow {A'B'} ;\overrightarrow {A'O'} } \right) = \frac{{\overrightarrow {A'B'} .\overrightarrow {A'O'} }}{{\left| {\overrightarrow {A'B'} } \right|.\left| {\overrightarrow {A'O'} } \right|}} = \frac{{\left( { - 120} \right)\left( { - 240} \right) + 0.0 + 300.0}}{{60\sqrt {29} .240}} = \frac{{2\sqrt {29} }}{{29}}\)
\( \Rightarrow \widehat {B'A'O'} \approx {68^0}\). Vậy \(\alpha \approx {68^0}\)
Trả lời câu hỏi Luyện tập 7 trang 72 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 7, khinh khí cầu thứ nhất hay thứ hai ở xa điểm xuất phát hơn? Giải thích vì sao.
Phương pháp giải:
Sử dụng kiến thức về tính độ dài của vectơ trong không gian: Trong không gian Oxyz, cho \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Lời giải chi tiết:
Theo Ví dụ 7 ta có, khinh khí cầu thứ nhất có tọa độ là A(2; 1; 0,5), khinh khí cầu thứ hai có tọa độ là \(B\left( { - 1; - 1,5;0,8} \right)\).
Ta có: \(OA = \sqrt {{2^2} + {1^2} + 0,{5^2}} = \frac{{\sqrt {21} }}{2}km\), \(OB = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1,5} \right)}^2} + 0,{8^2}} = \frac{{\sqrt {389} }}{{10}}km\).
Vì gốc O đặt tại điểm xuất phát và \(OA > OB\) nên khinh khí cầu thứ hai gần điểm xuất phát hơn.
Giải mục 3 trang 70, 71 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 3 trang 70, 71 SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương 1: Giới hạn. Đây là một phần quan trọng trong chương trình Toán 12, đặt nền móng cho các kiến thức về đạo hàm và tích phân trong các chương tiếp theo. Việc nắm vững các khái niệm và phương pháp giải bài tập trong mục này là vô cùng cần thiết để đạt kết quả tốt trong các kỳ thi.
Nội dung chính của Mục 3
- Ôn tập khái niệm giới hạn: Nhắc lại định nghĩa giới hạn của hàm số tại một điểm và giới hạn vô cực.
- Các dạng bài tập thường gặp: Tính giới hạn của hàm số, chứng minh sự tồn tại giới hạn, và ứng dụng giới hạn trong việc giải các bài toán thực tế.
- Phương pháp giải bài tập: Sử dụng các định lý về giới hạn, biến đổi đại số, và áp dụng quy tắc L'Hopital (nếu cần thiết).
Giải chi tiết các bài tập trong Mục 3
Dưới đây là lời giải chi tiết cho các bài tập trong mục 3 trang 70, 71 SGK Toán 12 tập 1 - Kết nối tri thức:
Bài 1: Tính các giới hạn sau
a) lim (x→2) (x^2 - 4) / (x - 2)
Lời giải: Ta có thể phân tích tử số thành (x - 2)(x + 2). Khi đó:
lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 4
b) lim (x→∞) (2x + 1) / (x - 3)
Lời giải: Chia cả tử và mẫu cho x, ta được:
lim (x→∞) (2x + 1) / (x - 3) = lim (x→∞) (2 + 1/x) / (1 - 3/x) = 2/1 = 2
Bài 2: Chứng minh rằng lim (x→0) sin(x) / x = 1
Lời giải: Đây là một giới hạn lượng giác cơ bản. Có nhiều cách để chứng minh, ví dụ sử dụng định lý kẹp hoặc quy tắc L'Hopital.
Bài 3: Ứng dụng giới hạn để giải bài toán về tốc độ thay đổi
Bài toán: Một vật chuyển động theo phương trình s(t) = t^2 + 2t. Tính vận tốc trung bình của vật trong khoảng thời gian từ t = 1 đến t = 3.
Lời giải: Vận tốc trung bình được tính bằng công thức (s(3) - s(1)) / (3 - 1). Thay các giá trị vào, ta được:
(s(3) - s(1)) / (3 - 1) = (3^2 + 2*3 - (1^2 + 2*1)) / 2 = (9 + 6 - 1 - 2) / 2 = 12 / 2 = 6
Mẹo học tốt và giải bài tập hiệu quả
- Nắm vững định nghĩa và các định lý về giới hạn.
- Luyện tập thường xuyên với nhiều dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học.
- Tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn.
Kết luận
Hy vọng rằng lời giải chi tiết và các hướng dẫn trên sẽ giúp các em học sinh hiểu rõ hơn về Mục 3 trang 70, 71 SGK Toán 12 tập 1 - Kết nối tri thức và tự tin giải các bài tập liên quan. Chúc các em học tập tốt!