Giải bài tập 3.14 trang 86 SGK Toán 12 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải Bài Tập 3.14 Trang 86 Toán 12 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với lời giải chi tiết bài tập 3.14 trang 86 SGK Toán 12 tập 1 Kết nối tri thức trên tusach.vn. Bài viết này sẽ cung cấp cho bạn phương pháp giải bài tập một cách dễ hiểu, cùng với đáp án chính xác.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, giúp các bạn học sinh học tập hiệu quả và đạt kết quả tốt nhất trong môn Toán.
Để đánh giá chất lượng một loại pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả như sau: Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Đề bài
Để đánh giá chất lượng một loại pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả như sau:
Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng biến thiên của mẫu số liệu ghép nhóm để tính:
Cho mẫu số liệu ghép nhóm:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = {a_{k + 1}} - {a_1}\).
+Sử dụng kiến thức về tính chất về nhóm chứa tứ phân vị của mẫu số liệu để tính: Ta có thể xác định nhóm chứa tứ phân vị thứ r nhờ tính chất: có khoảng \(\left( {\frac{{r.n}}{4}} \right)\) giá trị nhỏ hơn tứ phân vị này.
+ Sử dụng kiến thức về khoảng tứ phân vị của mẫu số liệu ghép nhóm để tính: Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
+ Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
+ Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \).
Lời giải chi tiết
Khoảng biến thiên: \(R = 7,5 - 5 = 2,5\)
Cỡ mẫu: \(n = 2 + 8 + 15 + 10 + 5 = 40\)
Tứ phân vị thứ nhất của mẫu số liệu là: \(\frac{{{x_{10}} + {x_{11}}}}{2}\), vì \({x_{10}} \in \left[ {5,5;6} \right),{x_{11}} \in \left[ {6;6,5} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 6\).
Tứ phân vị thứ ba của mẫu số liệu là: \(\frac{{{x_{30}} + {x_{31}}}}{2}\) thuộc nhóm \(\left[ {6,5;7} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 6,5 + \frac{{\frac{{3.40}}{4} - \left( {2 + 8 + 15} \right)}}{{10}}.0,5 = 6,75\).
Khoảng biến thiên: \({\Delta _Q} = {Q_3} - {Q_1} = 6,75 - 6 = 0,75\)
Chọn giá trị đại diện cho các nhóm số liệu, ta có: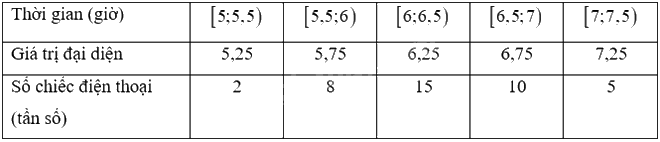
Thời gian trung bình nghe nhạc liên tục của điện thoại là: \(\overline x = \frac{1}{{40}}\left( {5,25.2 + 5,75.8 + 6,25.15 + 6,75.10 + 7,25.5} \right) = 6,35\)
Phương sai của mẫu số liệu là:
\({s^2} = \frac{1}{{40}}\left( {5,{{25}^2}.2 + 5,{{75}^2}.8 + 6,{{25}^2}.15 + 6,{{75}^2}.10 + 7,{{25}^2}.5} \right) - 6,{35^2} = 0,2775\)
Độ lệch chuẩn của mẫu số liệu là: \(\sqrt {0,2775} = \frac{{\sqrt {111} }}{{20}} \approx 0,53\)
Giải Bài Tập 3.14 Trang 86 Toán 12 Tập 1 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Bài tập 3.14 trang 86 SGK Toán 12 tập 1 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này thường liên quan đến việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Nội dung bài tập 3.14 trang 86 SGK Toán 12 Tập 1 - Kết Nối Tri Thức
(Giả sử nội dung bài tập là: Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Phương pháp giải
- Bước 1: Tìm tập xác định của hàm số. Trong trường hợp này, hàm số f(x) = x3 - 3x2 + 2 có tập xác định là R (tập hợp tất cả các số thực).
- Bước 2: Tính đạo hàm cấp một f'(x). f'(x) = 3x2 - 6x
- Bước 3: Tìm các điểm làm đạo hàm bằng 0 hoặc không xác định. Giải phương trình f'(x) = 0: 3x2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2.
- Bước 4: Lập bảng biến thiên. Xác định dấu của f'(x) trên các khoảng xác định bởi các điểm tìm được ở bước 3.
- Bước 5: Kết luận về các điểm cực trị. Dựa vào bảng biến thiên, xác định các điểm cực đại, cực tiểu của hàm số.
Lời giải chi tiết
Áp dụng các bước trên, ta có:
- Tập xác định: R
- Đạo hàm cấp một: f'(x) = 3x2 - 6x
- Các điểm làm đạo hàm bằng 0: x = 0 và x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Từ bảng biến thiên, ta thấy:
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu ý quan trọng
Khi giải các bài tập về đạo hàm, cần chú ý:
- Xác định đúng tập xác định của hàm số.
- Tính đạo hàm chính xác.
- Lập bảng biến thiên một cách cẩn thận.
- Kết luận đúng về các điểm cực trị.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 12 tập 1 Kết nối tri thức hoặc các đề thi thử.
Hy vọng bài giải này sẽ giúp bạn hiểu rõ hơn về cách giải bài tập 3.14 trang 86 SGK Toán 12 tập 1 Kết nối tri thức. Chúc bạn học tập tốt!