Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Lý thuyết Phương trình mặt phẳng Toán 12 Kết nối tri thức
SGK Toán 12 - Kết nối tri thức
Giải Toán 12 tập 2 - Kết nối tri thức
Chương 5. Phương pháp tọa độ trong không gian
Bài 14. Phương trình mặt phẳng

Lý thuyết Phương trình mặt phẳng Toán 12 Kết nối tri thức

Lý Thuyết Phương Trình Mặt Phẳng Toán 12 Kết Nối Tri Thức

Phương trình mặt phẳng là một trong những kiến thức quan trọng trong chương trình Toán 12 Kết Nối Tri Thức.

Nắm vững lý thuyết này giúp học sinh giải quyết các bài toán về hình học không gian một cách hiệu quả.

Tusach.vn cung cấp tài liệu học tập đầy đủ và dễ hiểu về phương trình mặt phẳng, giúp bạn tự tin chinh phục kỳ thi.

1. Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng a) Khái niệm vecto pháp tuyến

1. Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng

a) Khái niệm vecto pháp tuyến

Vecto \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vecto pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).

b) Tích có hướng của hai vecto

Trong không gian Oxyz, cho hai vecto \(\overrightarrow u = (a;b;c)\) và \(\overrightarrow v = (a';b';c')\). Khi đó vecto vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).

c) Cặp vecto chỉ phương

Trong không gian Oxyz, hai vecto \(\overrightarrow u \), \(\overrightarrow v \) được gọi là cặp vecto chỉ phương của mặt phẳng (P) nếu chúng không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P)

Nếu \(\overrightarrow u \), \(\overrightarrow v \) là cặp vecto chỉ phương của (P) thì \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) là một vecto pháp tuyến của (P).

2. Phương trình tổng quát của mặt phẳng

Trong không gian Oxyz, mỗi mặt phẳng đều có phương trình dạng Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng đó.

3. Lập phương trình tổng quát của mặt phẳng

Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\) có phương trình là:

\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0 \Leftrightarrow Ax + By + Cz + D = 0\), với \(D = - (A{x_0} + B{y_0} + C{z_0})\)

Bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vecto chỉ phương:

Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vecto chỉ phương \(\overrightarrow u \), \(\overrightarrow v \) có thể thực hiện theo các bước sau:

  • Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
  • Lập phương trình tổng quát của mặt phẳng đi qua M và biết vecto pháp tuyến \(\overrightarrow n \)

Bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng:

Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:

  • Tìm cặp vecto chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \).
  • Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
  • Lập phương trình tổng quát của mặt phẳng đi qua A và biết vecto pháp tuyến \(\overrightarrow n \)

4. Điều kiện để hai mặt phẳng vuông góc với nhau

Trong không gian Oxyz, cho hai mặt phẳng:

\(\left( \alpha \right):Ax + By + Cz + D = 0,\left( \beta \right):A'x + B'y + C'z + D' = 0,\) với hai vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\) tương ứng. Khi đó:

\(\left( \alpha \right) \bot \left( \beta \right) \Leftrightarrow \overrightarrow n \bot \overrightarrow {n'} \Leftrightarrow AA' + BB' + CC' = 0\).

5. Điều kiện để hai mặt phẳng song song với nhau

Trong không gian Oxyz, cho hai mặt phẳng:

\(\left( \alpha \right):Ax + By + Cz + D = 0,\left( \beta \right):A'x + B'y + C'z + D' = 0,\) với hai vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\) tương ứng. Khi đó:

\(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó.

6. Khoảng cách từ một điểm đến một mặt phẳng

Trong không gian Oxyz, khoảng cách từ điểm \({M_0}({x_0};{y_0};{z_0})\) đến mặt phẳng (P): Ax + By + Cz + D = 0 là:

\(d(M,(P)) = \frac{{\left| {A{x_0}{\rm{ }} + {\rm{ }}B{y_0}{\rm{ }} + {\rm{ }}C{z_0}{\rm{ }} + {\rm{ }}D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)

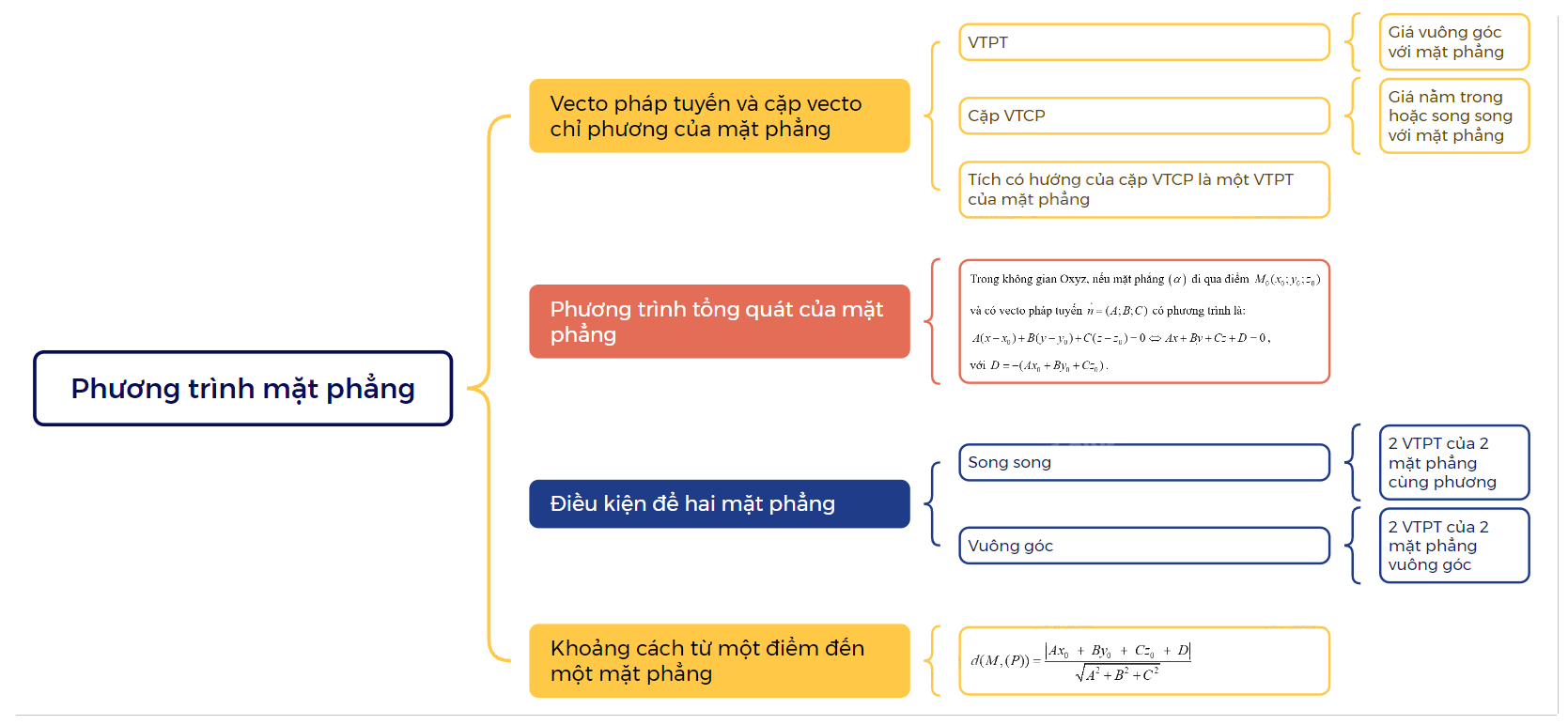
Lý thuyết Phương trình mặt phẳng Toán 12 Kết nối tri thức 1

Lý Thuyết Phương Trình Mặt Phẳng Toán 12 Kết Nối Tri Thức: Tổng Quan

Trong không gian Oxyz, một mặt phẳng được xác định duy nhất bởi một điểm thuộc mặt phẳng và một vectơ pháp tuyến của mặt phẳng đó. Phương trình mặt phẳng là một công cụ quan trọng để mô tả và nghiên cứu các mặt phẳng trong không gian.

1. Vectơ Pháp Tuyến của Mặt Phẳng

Vectơ pháp tuyến của mặt phẳng là một vectơ vuông góc với mọi vectơ nằm trong mặt phẳng. Nếu n = (a; b; c) là một vectơ pháp tuyến của mặt phẳng, thì phương trình của mặt phẳng có dạng:

a(x - x0) + b(y - y0) + c(z - z0) = 0

Trong đó (x0; y0; z0) là tọa độ của một điểm thuộc mặt phẳng.

2. Các Dạng Phương Trình Mặt Phẳng

  • Phương trình tổng quát của mặt phẳng: Ax + By + Cz + D = 0 (với A, B, C không đồng thời bằng 0).
  • Phương trình mặt phẳng khi biết một điểm và vectơ pháp tuyến: a(x - x0) + b(y - y0) + c(z - z0) = 0
  • Phương trình mặt phẳng khi biết ba điểm không thẳng hàng: Sử dụng định thức để tìm vectơ pháp tuyến.

3. Điều Kiện Mặt Phẳng Chứa Đường Thẳng

Để mặt phẳng (P): Ax + By + Cz + D = 0 chứa đường thẳng (d): {x = x0 + at, y = y0 + bt, z = z0 + ct}, cần và đủ là:

A(x0 + at) + B(y0 + bt) + C(z0 + ct) + D = 0 với mọi t.

Điều này tương đương với hệ phương trình:

  • Ax0 + By0 + Cz0 + D = 0
  • Aa + Bb + Cc = 0

4. Góc Giữa Hai Mặt Phẳng

Cho hai mặt phẳng (P1): A1x + B1y + C1z + D1 = 0 và (P2): A2x + B2y + C2z + D2 = 0. Gọi φ là góc giữa hai vectơ pháp tuyến n1 = (A1; B1; C1) và n2 = (A2; B2; C2). Khi đó:

cos φ = |n1 . n2| / (||n1|| . ||n2||)

Góc giữa hai mặt phẳng là góc nhọn hoặc góc tù nhỏ hơn hoặc bằng 90o.

5. Bài Tập Vận Dụng

Bài 1: Viết phương trình mặt phẳng đi qua điểm A(1; 2; 3) và có vectơ pháp tuyến n = (4; -5; 6).

Giải: Phương trình mặt phẳng là: 4(x - 1) - 5(y - 2) + 6(z - 3) = 0 <=> 4x - 5y + 6z - 15 = 0

Kết Luận

Lý thuyết phương trình mặt phẳng là nền tảng quan trọng để giải quyết các bài toán hình học không gian trong chương trình Toán 12 Kết Nối Tri Thức. Việc nắm vững các khái niệm, công thức và kỹ năng vận dụng sẽ giúp bạn đạt kết quả tốt trong các kỳ thi.

Tusach.vn hy vọng với tài liệu này, bạn sẽ học tập hiệu quả và tự tin hơn với môn Toán.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN