Xác suất có điều kiện
Cho hai biến cố A và B. Xác suất của biến cố A khi biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B và kí hiệu là P(A|B). Cho hai biến cố A và B bất kì, với P(B) > 0. Khi đó: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\) |
Ví dụ 1: Một hộp có 5 viên bi cùng kích thước và khối lượng, trong đó có 3 viên bi màu đỏ và 2 viên bi màu xanh. Lấy ngẫu nhiên lần lượt 2 viên bi và không hoàn lại. Tính xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ.
Giải:
GọiA là biến cố "Lấy được viên bi thứ hai có màu xanh";
B là biến cố "Lấy được viên bi thứ nhất có màu đỏ".
Khi đột xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ chính là xác suất của A với điều kiện B.
Vì một viên bi đỏ đã được lấy ra ở lần thứ nhất nên trong hợp còn lại 4 viên bi, trong đó có 2 viên bi xanh.
Từ đó ta có: \(P(A\mid B) = \frac{2}{4} = 0,5\).
Vậy xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ là 0,5.
Ví dụ 2: Trong cuộc khảo sát trên một nhóm học sinh gồm các bạn thích trà sữa hoặc kem, người ta có được kết quả sau: Có 56% số học sinh thích kem, 68% số học sinh thích trà sữa, 24% số học sinh thích cả trà sữa và kem. Chọn ngẫu nhiên một bạn học sinh trong nhóm được khảo sát này. Tính xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa.
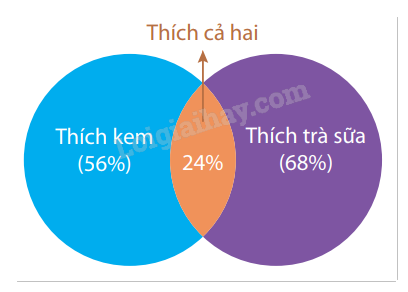
Giải:
Gọi: A là biến cố "Chọn được học sinh thích kem";
B là biến cố "Chọn được học sinh thích trà sữa".
Khi đó xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa chính là xác suất của A với điều kiện B.
Vì có 68% số học sinh thích trà sữa trong nhóm khảo sát nên P(B) = 68% = 0,68.
Ta có AB là biến cố "Chọn được học sinh thích cả trà sữa và kem".
Vì có 24% số học sinh thích cả trà sữa và kem nên P(AB) = 24% = 0,24.
Vì thế ta có: \(P(A\mid B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,24}}{{0,68}} = 0,35\).
Vậy xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa là 0,35.
Công thức nhân xác suất
Với hai biến cố A và B bất kì, ta có: \(P(AB) = P(B).P(A|B) = P(A).P(B|A)\) |
Ví dụ 3: Theo kết quả từ trạm nghiên cứu khí hậu tại địa phương T, xác suất để một ngày có gió là 0,6; nếu ngày có gió thì xác suất có mưa là 0,4; nếu ngày không có gió thì xác suất có mưa là 0,2. Gọi G là biến cố "Ngày có gió" và M là biến cố "Ngày có mưa".
a) Vẽ lại sơ đồ hình cây sau và điền vào ô ? các giá trị xác suất tương ứng:
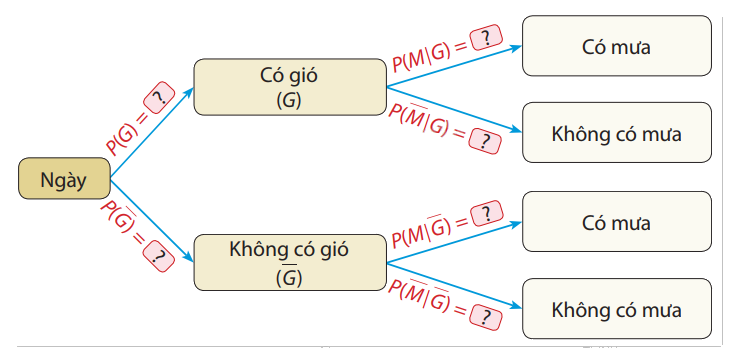
b) Tính xác suất P(GM) và \(P(G\overline M )\). Nêu ý nghĩa của các xác suất này.
Giải:
Theo đề bài, nếu ngày có gió thì xác suất có mưa là 0,4 nên \(P(M\mid G) = 0,4\). Suy ra: \(P(\overline M \mid G) = 1 - 0,4 = 0,6\).
Ngày không có gió thì xác suất có mưa là 0,2 nên \(P(M\mid \overline G ) = 0,2\).
Suy ra: \(P(\overline M \mid \overline G ) = 1 - 0,2 = 0,8\).
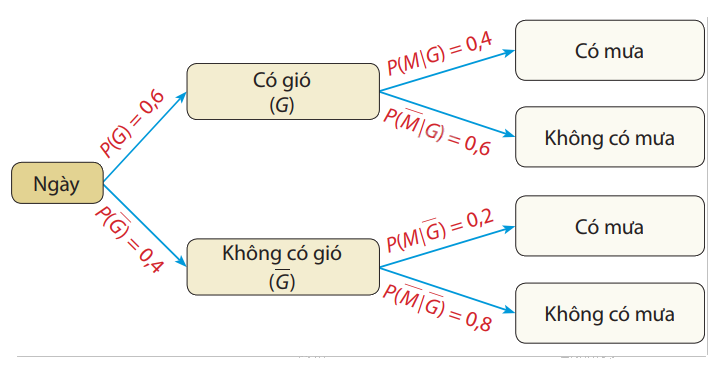
b) \(P(M\mid G) = P\left( G \right).P(M\mid G) = 0,6.0,4 = 0,24.\)
\(P(M\mid \overline G ) = P\left( G \right) \cdot P(M\mid G) = 0,6 \cdot 0,6 = 0,36.\)
Điều này có nghĩa là tại địa phương T, trong một ngày, xác suất để trời vừa có gió và vừa có mưa là 0,24; xác suất để trời có gió nhưng không có mưa là 0,36.
Nhận xét: Xác suất ở mỗi nhánh kể từ đỉnh thứ hai của sơ đồ hình cây là xác suất có điều kiện.
