Giải mục 3 trang 69, 70 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 69, 70 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết Giải mục 3 trang 69, 70 SGK Toán 12 tập 2. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu, giúp các em tự tin hơn trong quá trình học tập môn Toán.
Tusach.vn luôn đồng hành cùng các em, cung cấp tài liệu học tập chất lượng và hỗ trợ tối đa để các em đạt kết quả tốt nhất.
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
LT3
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa mặt phẳng \((\alpha ):\sqrt 3 x - y + 2 = 0\) và các mặt phẳng toạ độ \((Oxy)\), \((Oxz)\), \((Oyz)\).
Phương pháp giải:
- Xác định vectơ pháp tuyến của mặt phẳng \((\alpha )\).
- Góc giữa hai mặt phẳng là góc giữa các vectơ pháp tuyến của chúng:
\(\cos \theta = \frac{{{{\vec n}_1} \cdot {{\vec n}_2}}}{{|{{\vec n}_1}||{{\vec n}_2}|}}\)
Trong đó, \({\vec n_1} \cdot {\vec n_2}\) là tích vô hướng, \(|{\vec n_1}|\) và \(|{\vec n_2}|\) là độ lớn của các vectơ.
Lời giải chi tiết:
Cho mặt phẳng \((\alpha )\): \(\sqrt 3 x - y + 2 = 0\).
Vectơ pháp tuyến của mặt phẳng \(\alpha \): \({\vec n_\alpha } = (\sqrt 3 , - 1,0)\).
Góc giữa mặt phẳng \((\alpha )\) và Oxy:
- Vectơ pháp tuyến của Oxy: \({\vec n_{Oxy}} = (0,0,1)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxy}} = \sqrt 3 .0 + ( - 1).0 + 0.1 = 0\)
Độ lớn:
\(|{\vec n_\alpha }| = \sqrt {3 + 1 + 0} = 2,\quad |{\vec n_{Oxy}}| = \sqrt {0 + 0 + 1} = 1\)
\(\cos \theta = \frac{0}{{2 \times 1}} = 0\quad \Rightarrow \theta = {90^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oxz:
- Vectơ pháp tuyến của Oxz: \({\vec n_{Oxz}} = (0,1,0)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxz}} = \sqrt 3 .0 + ( - 1).1 + 0.0 = - 1\)
Độ lớn:
\(|{\vec n_{Oxz}}| = \sqrt {0 + 1 + 0} = 1\)
\(\cos \theta = \frac{{ - 1}}{{2 \times 1}} = - \frac{1}{2}\quad \Rightarrow \theta = {120^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oyz:
- Vectơ pháp tuyến của Oyz: \({\vec n_{Oyz}} = (1,0,0)\). Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oyz}} = \sqrt 3 .1 + ( - 1).0 + 0.0 = \sqrt 3 \)
Độ lớn:
\(|{\vec n_{Oyz}}| = \sqrt {1 + 0 + 0} = 1\)
\(\cos \theta = \frac{{\sqrt 3 }}{{2 \times 1}} = \frac{{\sqrt 3 }}{2}\quad \Rightarrow \theta = {30^\circ }\)
VD
Trả lời câu hỏi Vận dụng trang 70 SGK Toán 12 Cùng khám phá
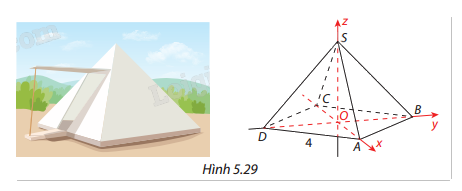
Để chuẩn bị cho chuyến đi dã ngoại, nhóm bạn Đức thiết kế lều cắm trại dạng hình chóp từ giác đều có đáy là hình vuông cạnh 4m. Theo bản vẽ thiết kế thì góc giữa hai mặt bên của lều bằng 60°. Bằng phương pháp tọa độ, hãy tính chiều cao của lều này.
Phương pháp giải:
- Xây dựng hệ tọa độ và xác định tọa độ các điểm
- Xác định vector pháp tuyến của các mặt bên
- Sử dụng công thức tính góc giữa hai mặt phẳng qua vector pháp tuyến
- Giải phương trình để tìm chiều cao
Lời giải chi tiết:
Gọi h là chiều cao cần tìm của hình chóp S.ABCD.
Do mặt đáy là hình vuông cạnh 4m nên \(OA = OB = OC = OD = 2\sqrt 2 \)
Toạ độ các điểm là \(A(2\sqrt 2 ;0;0)\), \(B(0;2\sqrt 2 ;0)\), \(C( - 2\sqrt 2 ;0;0)\), \(D(0; - 2\sqrt 2 ;0)\) và \(S(0;0;h)\).
Vectơ chỉ phương của mặt phẳng SAB là \(\overrightarrow {AB} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SA} = (2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SAB là
\(\overrightarrow {{n_{SAB}}} = \overrightarrow {AB} .\overrightarrow {SA} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.2\sqrt 2 - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .2\sqrt 2 = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h; - 8)\)
Vectơ chỉ phương của mặt phẳng SCD là \(\overrightarrow {DC} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SC} = ( - 2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SCD là
\(\overrightarrow {{n_{SCD}}} = \overrightarrow {DC} .\overrightarrow {SC} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.( - 2\sqrt 2 ) - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .( - 2\sqrt 2 )) = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h;8)\)
Ta có:
\(\overrightarrow {{n_{SAB}}} .\overrightarrow {{n_{SCD}}} = 8{h^2} + 8{h^2} - 64 = 16{h^2} - 64 = 16({h^2} - 4)\)
\(\left| {\overrightarrow {{n_{SAB}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
\(\left| {\overrightarrow {{n_{SCD}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
Góc giữa hai mặt phẳng SAB và SCD bằng 60° nên suy ra:
\(\cos 60^\circ = \frac{{16({h^2} - 4)}}{{4\sqrt {{h^2} + 4} .4\sqrt {{h^2} + 4} }} = \frac{{16({h^2} - 4)}}{{16({h^2} + 4)}} = \frac{{{h^2} - 4}}{{{h^2} + 4}} = \frac{1}{2}\)
\( \Leftrightarrow 2{h^2} - 8 = {h^2} + 4\)
\( \Leftrightarrow {h^2} = 12\)
\( \Leftrightarrow h = \sqrt {12} = 2\sqrt 3 \)
Vậy chiều cao của lều là \(2\sqrt 3 \)m.
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 69 SGK Toán 12 Cùng khám phá
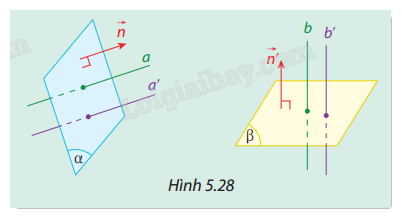
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
Phương pháp giải:
Sử dụng tính chất góc giữa hai đường thẳng sẽ bằng góc giữa hai vectơ chỉ phương của chúng.
Lời giải chi tiết:
Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\vec n\), và của mặt phẳng \((\beta )\) là \(\vec n'\).
Nếu hai đường thẳng \(a\) và \(a'\) vuông góc với \((\alpha )\), và \(b\) và \(b'\) vuông góc với \((\beta )\), thì hai vectơ \(\vec n\) và \(\vec n'\)lần lượt là hai vectơ chỉ phương của \(a\) và \(a'\), \(b\) và \(b'\).
Mà góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của chúng nên
\((a,b) = (a',b')\) do cùng bằng với góc \((\overrightarrow n ,\overrightarrow {n'} )\).
Vậy nếu \(\vec a\) vuông góc với \((\alpha )\) và \(\vec b\) vuông góc với \((\beta )\), thì hai góc \((a,b)\) và \((a',b')\) sẽ bằng nhau vì cùng liên quan đến vectơ pháp tuyến \(\vec n\) và \(\vec n'\).
- HĐ3
- LT3
- VD
Trả lời câu hỏi Hoạt động 3 trang 69 SGK Toán 12 Cùng khám phá
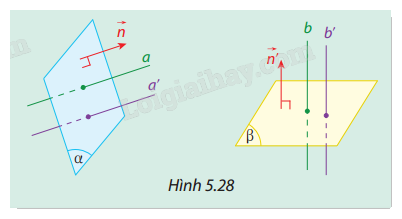
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
Phương pháp giải:
Sử dụng tính chất góc giữa hai đường thẳng sẽ bằng góc giữa hai vectơ chỉ phương của chúng.
Lời giải chi tiết:
Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\vec n\), và của mặt phẳng \((\beta )\) là \(\vec n'\).
Nếu hai đường thẳng \(a\) và \(a'\) vuông góc với \((\alpha )\), và \(b\) và \(b'\) vuông góc với \((\beta )\), thì hai vectơ \(\vec n\) và \(\vec n'\)lần lượt là hai vectơ chỉ phương của \(a\) và \(a'\), \(b\) và \(b'\).
Mà góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của chúng nên
\((a,b) = (a',b')\) do cùng bằng với góc \((\overrightarrow n ,\overrightarrow {n'} )\).
Vậy nếu \(\vec a\) vuông góc với \((\alpha )\) và \(\vec b\) vuông góc với \((\beta )\), thì hai góc \((a,b)\) và \((a',b')\) sẽ bằng nhau vì cùng liên quan đến vectơ pháp tuyến \(\vec n\) và \(\vec n'\).
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa mặt phẳng \((\alpha ):\sqrt 3 x - y + 2 = 0\) và các mặt phẳng toạ độ \((Oxy)\), \((Oxz)\), \((Oyz)\).
Phương pháp giải:
- Xác định vectơ pháp tuyến của mặt phẳng \((\alpha )\).
- Góc giữa hai mặt phẳng là góc giữa các vectơ pháp tuyến của chúng:
\(\cos \theta = \frac{{{{\vec n}_1} \cdot {{\vec n}_2}}}{{|{{\vec n}_1}||{{\vec n}_2}|}}\)
Trong đó, \({\vec n_1} \cdot {\vec n_2}\) là tích vô hướng, \(|{\vec n_1}|\) và \(|{\vec n_2}|\) là độ lớn của các vectơ.
Lời giải chi tiết:
Cho mặt phẳng \((\alpha )\): \(\sqrt 3 x - y + 2 = 0\).
Vectơ pháp tuyến của mặt phẳng \(\alpha \): \({\vec n_\alpha } = (\sqrt 3 , - 1,0)\).
Góc giữa mặt phẳng \((\alpha )\) và Oxy:
- Vectơ pháp tuyến của Oxy: \({\vec n_{Oxy}} = (0,0,1)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxy}} = \sqrt 3 .0 + ( - 1).0 + 0.1 = 0\)
Độ lớn:
\(|{\vec n_\alpha }| = \sqrt {3 + 1 + 0} = 2,\quad |{\vec n_{Oxy}}| = \sqrt {0 + 0 + 1} = 1\)
\(\cos \theta = \frac{0}{{2 \times 1}} = 0\quad \Rightarrow \theta = {90^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oxz:
- Vectơ pháp tuyến của Oxz: \({\vec n_{Oxz}} = (0,1,0)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxz}} = \sqrt 3 .0 + ( - 1).1 + 0.0 = - 1\)
Độ lớn:
\(|{\vec n_{Oxz}}| = \sqrt {0 + 1 + 0} = 1\)
\(\cos \theta = \frac{{ - 1}}{{2 \times 1}} = - \frac{1}{2}\quad \Rightarrow \theta = {120^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oyz:
- Vectơ pháp tuyến của Oyz: \({\vec n_{Oyz}} = (1,0,0)\). Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oyz}} = \sqrt 3 .1 + ( - 1).0 + 0.0 = \sqrt 3 \)
Độ lớn:
\(|{\vec n_{Oyz}}| = \sqrt {1 + 0 + 0} = 1\)
\(\cos \theta = \frac{{\sqrt 3 }}{{2 \times 1}} = \frac{{\sqrt 3 }}{2}\quad \Rightarrow \theta = {30^\circ }\)
Trả lời câu hỏi Vận dụng trang 70 SGK Toán 12 Cùng khám phá
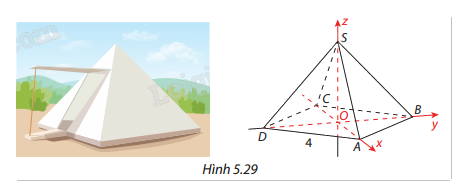
Để chuẩn bị cho chuyến đi dã ngoại, nhóm bạn Đức thiết kế lều cắm trại dạng hình chóp từ giác đều có đáy là hình vuông cạnh 4m. Theo bản vẽ thiết kế thì góc giữa hai mặt bên của lều bằng 60°. Bằng phương pháp tọa độ, hãy tính chiều cao của lều này.
Phương pháp giải:
- Xây dựng hệ tọa độ và xác định tọa độ các điểm
- Xác định vector pháp tuyến của các mặt bên
- Sử dụng công thức tính góc giữa hai mặt phẳng qua vector pháp tuyến
- Giải phương trình để tìm chiều cao
Lời giải chi tiết:
Gọi h là chiều cao cần tìm của hình chóp S.ABCD.
Do mặt đáy là hình vuông cạnh 4m nên \(OA = OB = OC = OD = 2\sqrt 2 \)
Toạ độ các điểm là \(A(2\sqrt 2 ;0;0)\), \(B(0;2\sqrt 2 ;0)\), \(C( - 2\sqrt 2 ;0;0)\), \(D(0; - 2\sqrt 2 ;0)\) và \(S(0;0;h)\).
Vectơ chỉ phương của mặt phẳng SAB là \(\overrightarrow {AB} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SA} = (2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SAB là
\(\overrightarrow {{n_{SAB}}} = \overrightarrow {AB} .\overrightarrow {SA} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.2\sqrt 2 - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .2\sqrt 2 = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h; - 8)\)
Vectơ chỉ phương của mặt phẳng SCD là \(\overrightarrow {DC} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SC} = ( - 2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SCD là
\(\overrightarrow {{n_{SCD}}} = \overrightarrow {DC} .\overrightarrow {SC} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.( - 2\sqrt 2 ) - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .( - 2\sqrt 2 )) = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h;8)\)
Ta có:
\(\overrightarrow {{n_{SAB}}} .\overrightarrow {{n_{SCD}}} = 8{h^2} + 8{h^2} - 64 = 16{h^2} - 64 = 16({h^2} - 4)\)
\(\left| {\overrightarrow {{n_{SAB}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
\(\left| {\overrightarrow {{n_{SCD}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
Góc giữa hai mặt phẳng SAB và SCD bằng 60° nên suy ra:
\(\cos 60^\circ = \frac{{16({h^2} - 4)}}{{4\sqrt {{h^2} + 4} .4\sqrt {{h^2} + 4} }} = \frac{{16({h^2} - 4)}}{{16({h^2} + 4)}} = \frac{{{h^2} - 4}}{{{h^2} + 4}} = \frac{1}{2}\)
\( \Leftrightarrow 2{h^2} - 8 = {h^2} + 4\)
\( \Leftrightarrow {h^2} = 12\)
\( \Leftrightarrow h = \sqrt {12} = 2\sqrt 3 \)
Vậy chiều cao của lều là \(2\sqrt 3 \)m.
Giải mục 3 trang 69, 70 SGK Toán 12 tập 2: Tổng quan và Phương pháp tiếp cận
Mục 3 trang 69, 70 SGK Toán 12 tập 2 thường xoay quanh các chủ đề về Đường thẳng và Mặt phẳng trong không gian, cụ thể là các bài toán liên quan đến quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng. Để giải tốt các bài toán này, học sinh cần nắm vững các kiến thức cơ bản sau:
- Định nghĩa và tính chất của đường thẳng song song, vuông góc với mặt phẳng.
- Điều kiện để hai đường thẳng song song, vuông góc.
- Điều kiện để hai mặt phẳng song song, vuông góc.
- Các định lý về đường thẳng vuông góc với mặt phẳng.
- Phương pháp tìm giao tuyến của hai mặt phẳng.
Giải chi tiết các bài tập trong mục 3 trang 69, 70
Dưới đây là giải chi tiết các bài tập thường gặp trong mục 3 trang 69, 70 SGK Toán 12 tập 2. Lưu ý rằng, mỗi bài tập có thể có nhiều cách giải khác nhau, chúng ta sẽ trình bày một cách giải phổ biến và dễ hiểu nhất.
Bài 1: Chứng minh sự song song
Bài tập thường yêu cầu chứng minh một đường thẳng song song với một mặt phẳng hoặc hai đường thẳng song song với nhau. Để giải quyết bài toán này, học sinh cần sử dụng các định lý và tính chất đã học. Ví dụ:
Đề bài: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM song song với mặt phẳng (SCD).
Lời giải:
- Tìm giao điểm của AM và mặt phẳng (SCD).
- Chứng minh giao điểm này thuộc đường thẳng CD.
- Kết luận AM song song với mặt phẳng (SCD).
Bài 2: Chứng minh sự vuông góc
Bài tập thường yêu cầu chứng minh một đường thẳng vuông góc với một mặt phẳng hoặc hai mặt phẳng vuông góc với nhau. Để giải quyết bài toán này, học sinh cần sử dụng các định lý và tính chất về đường thẳng vuông góc với mặt phẳng.
Đề bài: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Chứng minh rằng SA vuông góc với BC.
Lời giải:
Vì SA vuông góc với mặt phẳng (ABC) và BC là một đường thẳng nằm trong mặt phẳng (ABC) nên SA vuông góc với BC.
Bài 3: Tính góc giữa đường thẳng và mặt phẳng
Bài tập thường yêu cầu tính góc giữa một đường thẳng và một mặt phẳng. Để giải quyết bài toán này, học sinh cần sử dụng công thức tính góc giữa đường thẳng và mặt phẳng.
Công thức: Góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và hình chiếu của d lên mặt phẳng (P).
Mẹo học tập và luyện tập hiệu quả
Để học tốt môn Toán 12, đặc biệt là phần hình học không gian, học sinh cần:
- Nắm vững các định nghĩa, tính chất, định lý.
- Vẽ hình minh họa để hình dung rõ hơn về bài toán.
- Luyện tập thường xuyên các bài tập từ dễ đến khó.
- Tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn.
Tusach.vn – Người bạn đồng hành đáng tin cậy
Tusach.vn tự hào là một trong những website cung cấp tài liệu học tập Toán 12 uy tín và chất lượng nhất. Chúng tôi luôn cập nhật những lời giải chi tiết, dễ hiểu và phương pháp giải bài tập hiệu quả, giúp các em học sinh đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chủ đề | Liên kết |
|---|---|
| Giải Toán 12 tập 1 | Link tập 1 |
| Giải Toán 12 tập 2 | Link tập 2 |