Giải bài tập 1.33 trang 46 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 1.33 Trang 46 Toán 12 Tập 1
Bài tập 1.33 trang 46 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này thường liên quan đến việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và kỹ năng giải toán.
Cho hàm số \(y = \frac{{2{x^2}}}{{{x^2} - 1}}\) có đồ thị là đường cong như Hình 1.67. Xác định các đường tiệm cận đứng, tiệm cận ngang và tiệm cận xiên (nếu có) của đồ thị hàm số đã cho.
Đề bài
Cho hàm số \(y = \frac{{2{x^2}}}{{{x^2} - 1}}\) có đồ thị là đường cong như Hình 1.67. Xác định các đường tiệm cận đứng, tiệm cận ngang và tiệm cận xiên (nếu có) của đồ thị hàm số đã cho.
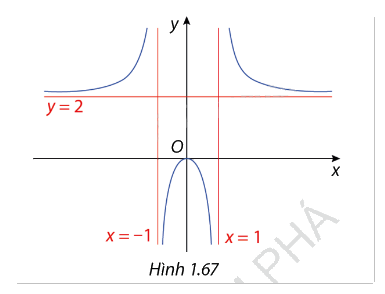
Phương pháp giải - Xem chi tiết
Nhìn vào đồ thị và tìm đường thẳng thoả mãn các điều kiện sau:
- Tiệm cận đứng: Có dạng x = a, giá trị của hàm số sẽ tiến tới vô cực khi x tiến dần đến a.
- Tiệm cận ngang: Có dạng y = k, đồ thị của hàm số tiến dần đến k khi x tiến ra vô cực.
- Tiệm cận xiên: Có dạng y = ax+b, không tồn tại song song với tiệm cận ngang.
Lời giải chi tiết
- Tiệm cận đứng: \(x = \pm 1\)
- Tiệm cận ngang: \(y = 2\)
- Tiệm cận xiên: Không tồn tại vì hàm số đã có tiệm cận ngang.
Giải Bài Tập 1.33 Trang 46 SGK Toán 12 Tập 1: Hướng Dẫn Chi Tiết
Bài tập 1.33 trang 46 SGK Toán 12 tập 1 thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tiếp tuyến của đường cong, cực trị của hàm số, hoặc các bài toán tối ưu hóa. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức đạo hàm cơ bản.
Phân Tích Đề Bài và Xác Định Yêu Cầu
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh những sai sót không đáng có.
Phương Pháp Giải Bài Tập 1.33 Trang 46
Thông thường, để giải bài tập 1.33 trang 46, chúng ta cần thực hiện các bước sau:
- Tính đạo hàm: Tính đạo hàm của hàm số đã cho.
- Tìm điều kiện cần: Tìm các điểm mà đạo hàm bằng 0 hoặc không xác định. Đây là các điểm nghi ngờ là điểm cực trị hoặc điểm uốn.
- Xét dấu đạo hàm: Xét dấu đạo hàm trên các khoảng xác định để xác định khoảng hàm số đồng biến, nghịch biến.
- Kết luận: Dựa vào kết quả xét dấu đạo hàm, kết luận về tính đơn điệu của hàm số và các điểm cực trị.
Ví Dụ Minh Họa (Giả định đề bài cụ thể)
Giả sử đề bài: Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Giải:
- Bước 1: Tính đạo hàm: y' = 3x2 - 6x
- Bước 2: Tìm điều kiện cần: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Bước 3: Xét dấu đạo hàm:
x -∞ 0 2 +∞ y' + - + y Đồng biến Nghịch biến Đồng biến - Bước 4: Kết luận: Hàm số đạt cực đại tại x = 0, ycđ = 2 và đạt cực tiểu tại x = 2, yct = -2.
Lưu Ý Quan Trọng
Khi giải bài tập về đạo hàm, cần chú ý các điểm sau:
- Kiểm tra kỹ điều kiện xác định của hàm số.
- Sử dụng đúng các công thức đạo hàm cơ bản.
- Phân tích kết quả một cách cẩn thận để đưa ra kết luận chính xác.
Tusach.vn - Nguồn Tài Liệu Toán Học Uy Tín
tusach.vn là một nguồn tài liệu toán học uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong SGK Toán 12 tập 1 và các tài liệu tham khảo khác. Chúng tôi hy vọng rằng với những hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán về đạo hàm và đạt kết quả tốt trong môn Toán.
Hãy truy cập tusach.vn thường xuyên để cập nhật những kiến thức và kỹ năng giải toán mới nhất!