Giải mục 3 trang 70, 71, 72 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 70, 71, 72 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 70, 71, 72 SGK Toán 12 tập 1 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, tusach.vn đã biên soạn bộ giải bài tập Toán 12 tập 1 đầy đủ và chính xác.
Trong không gian Oxyz, cho vectơ (vec a). a) Xác định điểm M sao cho (overrightarrow {OM} = vec a). b) Gọi (left( {x;y;z} right)) là toạ độ của điểm M. Hãy biểu diễn (vec a) theo ba vectơ đơn vị (vec i,vec j,vec k).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho vectơ \(\vec a\).
a) Xác định điểm M sao cho \(\overrightarrow {OM} = \vec a\).
b) Gọi \(\left( {x;y;z} \right)\) là toạ độ của điểm M. Hãy biểu diễn \(\vec a\) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\).
Phương pháp giải:
- Giả sử vectơ \(\vec a\) có tọa độ \(({a_1},{a_2},{a_3})\). Điểm \(M\) cần tìm sẽ có tọa độ \(({a_1},{a_2},{a_3})\) để thỏa mãn \(\overrightarrow {OM} = \vec a\).
- Biểu diễn của \(\overrightarrow a \) sẽ giống như biểu diễn \(\overrightarrow {OM} \).
Lời giải chi tiết:
a) Xác định điểm M:
- Vector \(\overrightarrow {OM} \) là vector có điểm đầu tại gốc tọa độ \(O(0,0,0)\) và điểm cuối tại điểm \(M(x,y,z)\). Do đó, \(\overrightarrow {OM} \) có dạng:
\(\overrightarrow {OM} = \overrightarrow {OM} = (x - 0)\vec i + (y - 0)\vec j + (z - 0)\vec k = x\vec i + y\vec j + z\overrightarrow k \)
- Nếu \(\overrightarrow {OM} = \vec a\), thì tọa độ của điểm M chính là các thành phần của vector \(\vec a\). Giả sử vector \(\vec a\) có dạng \(\vec a = \left( {{a_1},{a_2},{a_3}} \right)\), thì: \(M\left( {{a_1},{a_2},{a_3}} \right)\)
- Như vậy, điểm M có tọa độ \(\left( {{a_1},{a_2},{a_3}} \right)\)
b) Biểu diễn \(\vec a\) theo các vector đơn vị \(\vec i,\vec j,\vec k\)
- Gọi \((x,y,z)\) là tọa độ của điểm M. Như đã phân tích ở phần a, vector \(\overrightarrow {OM} \) có dạng: \(\overrightarrow {OM} = x\vec i + y\vec j + z\vec k\)
- Do \(\overrightarrow {OM} = \vec a\), ta có: \(\vec a = x\vec i + y\vec j + z\vec k\)
- Như vậy vector \(\vec a\) có thể biểu diễn theo các vector đơn vị \(\vec i,\vec j,\vec k\) dưới dạng:
\(\vec a = {a_1}\vec i + {a_2}\vec j + {a_3}\vec k\)
LT4
Trả lời câu hỏi Luyện tập 4 trang 71 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba vectơ \(\vec a = \left( { - 1;0;3} \right),\vec b = \left( {2;1;0} \right),\vec c = \left( { - 2;3;5} \right)\). Tìm toạ độ của \(\vec x = 2\vec a - \frac{1}{2}\vec b - 3\vec c\).
Phương pháp giải:
Tính toán các thành phần của vectơ đã cho rồi cộng chúng lại.
Lời giải chi tiết:
Tính toán từng vectơ thành phần của \(\vec x\):\(2\vec a = 2 \times \left( { - 1,0,3} \right) = \left( { - 2,0,6} \right), - \frac{1}{2}\vec b = - \frac{1}{2} \times \left( {2,1,0} \right) = \left( { - 1, - \frac{1}{2},0} \right), - 3\vec c = - 3 \times \left( { - 2,3,5} \right) = \left( {6, - 9, - 15} \right).\)
Cộng các vectơ thành phần để tìm tọa độ của \(\vec x\):
\(\vec x = \left( { - 2,0,6} \right) + \left( { - 1, - \frac{1}{2},0} \right) + \left( {6, - 9, - 15} \right)\).
Tọa độ của \(\vec x\) là:
\(x = - 2 - 1 + 6 = 3,y = 0 - \frac{1}{2} - 9 = - \frac{{19}}{2},z = 6 + 0 - 15 = - 9.\)
Vậy, tọa độ của vectơ \(\vec x\) là \(\left( {3, - \frac{{19}}{2}, - 9} \right)\).
VD
Trả lời câu hỏi Vận dụng trang 72 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz,\),một vật đi từ điểm \(A(2;3;0)\) đến điểm \(B( - 1;1;2)\) rồi tiếp tục đi đến điểm \(C(3; - 2; - 1)\). Tìm vectơ biểu thị độ dịch chuyển của vật khi:
a) Vật đi từ điểm \(A\) đến điểm \(B\);
b) Vật đi từ điểm \(A\) đến điểm \(C\).
Phương pháp giải:
- Để tìm vectơ biểu thị độ dịch chuyển của vật, ta sử dụng công thức tính vectơ từ một điểm này đến một điểm khác trong không gian ba chiều.
- Vectơ độ dịch chuyển từ điểm \(A\) đến điểm \(B\) được tính bằng tọa độ điểm \(B\) trừ đi tọa độ điểm \(A\).
- Tương tự, vectơ độ dịch chuyển từ điểm \(A\) đến điểm \(C\) được tính bằng tọa độ điểm \(C\) trừ đi tọa độ điểm \(A\).
Lời giải chi tiết:
a) Vectơ độ dịch chuyển của vật khi đi từ \(A\) đến \(B\):
Vectơ \(\overrightarrow {AB} \) được tính bằng công thức:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AB} = ( - 1 - 2;1 - 3;2 - 0) = ( - 3; - 2;2)\)
Vậy vectơ độ dịch chuyển từ \(A\) đến \(B\) là \(\overrightarrow {AB} = ( - 3; - 2;2)\).
b) Vectơ độ dịch chuyển của vật khi đi từ \(A\) đến \(C\):
Vectơ \(\overrightarrow {AC} \) được tính bằng công thức:
\(\overrightarrow {AC} = ({x_C} - {x_A};{y_C} - {y_A};{z_C} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AC}= (3 - 2; - 2 - 3; - 1 - 0) = (1; - 5; - 1)\)
Vậy vectơ độ dịch chuyển từ \(A\) đến \(C\) là \(\overrightarrow {AC} = (1; - 5; - 1)\).
LT5
Trả lời câu hỏi Luyện tập 5 trang 72 SGK Toán 12 Cùng khám phá
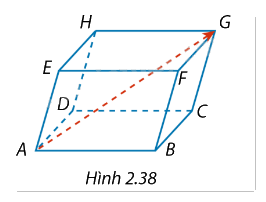
Trong không gian Oxyz, cho hình hộp ABCD.EFGH có A(1; 0; -1), B(2; 1; 3) và H(4; 3; 4) (Hình 2.38).
a) Tìm tọa độ của đỉnh G.
b) Tìm tọa độ của \(\overrightarrow {AG} \).
Phương pháp giải:
- Sử dụng các tính chất của hình hộp chữ nhật trong không gian, đặc biệt là các quy tắc liên quan đến tọa độ của các đỉnh dựa trên tính chất đối xứng và các đường chéo.
- Áp dụng công thức sau để tính toạ độ vectơ trong không gian.
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A}} \right)\)
Lời giải chi tiết:
a) Tìm toạ độ của điểm G
Vì ABCD.EFGH là một hình hộp, nên G là đỉnh đối diện với A và \(\overrightarrow {HG} = \overrightarrow {AB} \).
Mà \(\overrightarrow {HG} = \overrightarrow {OG} - \overrightarrow {OH} \) nên suy ra \(\overrightarrow {OG} = \overrightarrow {AB} + \overrightarrow {OH} \)
Do đó, tọa độ của G được tính bằng cách lấy toạ độ của vectơ \(\overrightarrow {AB} \) cộng tọa độ của điểm H hay nói cách khác là lấy toạ độ của điểm B cộng với tọa độ của điểm H trừ đi tọa độ của điểm A: \(G = B + H - A\)
Tính toán cụ thể: \(G = (2,1,3) + (4,3,4) - (1,0, - 1) = (5,4,8)\)
Vậy tọa độ của điểm \(G\) là \((5,4,8)\).
b) Tìm tọa độ của \(\overrightarrow {AG} \):
Tọa độ của vectơ \(\overrightarrow {AG} \) được tính bằng tọa độ của G trừ tọa độ của A:
\(\overrightarrow {AG} = ({x_G} - {x_A},{y_G} - {y_A},{z_G} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AG} = (5 - 1,4 - 0,8 - ( - 1)) = (4,4,9)\)
Vậy tọa độ của \(\overrightarrow {AG} \) là \((4,4,9)\).
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 71 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hai điểm \(M({x_M},{y_M},{z_M})\) và \(N({x_N},{y_N},{z_N})\) (Hình 2.36).
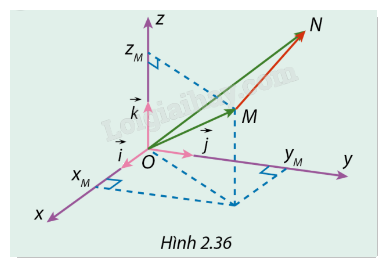
a) Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \).
b) Biểu diễn mỗi vectơ \(\overrightarrow {OM} \), \(\overrightarrow {ON} \) qua các vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\).
c) Chứng minh rằng \(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\).
Phương pháp giải:
- Sử dụng định nghĩa và tính chất của vectơ trong không gian.
- Sử dụng biểu thức của vectơ trong hệ tọa độ Oxyz qua các vectơ đơn vị \(\vec i\), \(\vec j\),\(\vec k\).
Lời giải chi tiết:
a) Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \):
Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \)
b) Biểu diễn mỗi vectơ \(\overrightarrow {OM} \), \(\overrightarrow {ON} \) qua các vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\):
Với các tọa độ đã cho:
\(\overrightarrow {OM} = {x_M}\vec i + {y_M}\vec j + {z_M}\vec k\)
\(\overrightarrow {ON} = {x_N}\vec i + {y_N}\vec j + {z_N}\vec k\)
c) Chứng minh rằng \(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\):
Dùng kết quả của phần (a) và (b): \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = ({x_N}\vec i + {y_N}\vec j + {z_N}\vec k) - ({x_M}\vec i + {y_M}\vec j + {z_M}\vec k)\)
Kết quả:
\(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\)
- HĐ3
- LT4
- HĐ4
- LT5
- VD
Trả lời câu hỏi Hoạt động 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho vectơ \(\vec a\).
a) Xác định điểm M sao cho \(\overrightarrow {OM} = \vec a\).
b) Gọi \(\left( {x;y;z} \right)\) là toạ độ của điểm M. Hãy biểu diễn \(\vec a\) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\).
Phương pháp giải:
- Giả sử vectơ \(\vec a\) có tọa độ \(({a_1},{a_2},{a_3})\). Điểm \(M\) cần tìm sẽ có tọa độ \(({a_1},{a_2},{a_3})\) để thỏa mãn \(\overrightarrow {OM} = \vec a\).
- Biểu diễn của \(\overrightarrow a \) sẽ giống như biểu diễn \(\overrightarrow {OM} \).
Lời giải chi tiết:
a) Xác định điểm M:
- Vector \(\overrightarrow {OM} \) là vector có điểm đầu tại gốc tọa độ \(O(0,0,0)\) và điểm cuối tại điểm \(M(x,y,z)\). Do đó, \(\overrightarrow {OM} \) có dạng:
\(\overrightarrow {OM} = \overrightarrow {OM} = (x - 0)\vec i + (y - 0)\vec j + (z - 0)\vec k = x\vec i + y\vec j + z\overrightarrow k \)
- Nếu \(\overrightarrow {OM} = \vec a\), thì tọa độ của điểm M chính là các thành phần của vector \(\vec a\). Giả sử vector \(\vec a\) có dạng \(\vec a = \left( {{a_1},{a_2},{a_3}} \right)\), thì: \(M\left( {{a_1},{a_2},{a_3}} \right)\)
- Như vậy, điểm M có tọa độ \(\left( {{a_1},{a_2},{a_3}} \right)\)
b) Biểu diễn \(\vec a\) theo các vector đơn vị \(\vec i,\vec j,\vec k\)
- Gọi \((x,y,z)\) là tọa độ của điểm M. Như đã phân tích ở phần a, vector \(\overrightarrow {OM} \) có dạng: \(\overrightarrow {OM} = x\vec i + y\vec j + z\vec k\)
- Do \(\overrightarrow {OM} = \vec a\), ta có: \(\vec a = x\vec i + y\vec j + z\vec k\)
- Như vậy vector \(\vec a\) có thể biểu diễn theo các vector đơn vị \(\vec i,\vec j,\vec k\) dưới dạng:
\(\vec a = {a_1}\vec i + {a_2}\vec j + {a_3}\vec k\)
Trả lời câu hỏi Luyện tập 4 trang 71 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba vectơ \(\vec a = \left( { - 1;0;3} \right),\vec b = \left( {2;1;0} \right),\vec c = \left( { - 2;3;5} \right)\). Tìm toạ độ của \(\vec x = 2\vec a - \frac{1}{2}\vec b - 3\vec c\).
Phương pháp giải:
Tính toán các thành phần của vectơ đã cho rồi cộng chúng lại.
Lời giải chi tiết:
Tính toán từng vectơ thành phần của \(\vec x\):\(2\vec a = 2 \times \left( { - 1,0,3} \right) = \left( { - 2,0,6} \right), - \frac{1}{2}\vec b = - \frac{1}{2} \times \left( {2,1,0} \right) = \left( { - 1, - \frac{1}{2},0} \right), - 3\vec c = - 3 \times \left( { - 2,3,5} \right) = \left( {6, - 9, - 15} \right).\)
Cộng các vectơ thành phần để tìm tọa độ của \(\vec x\):
\(\vec x = \left( { - 2,0,6} \right) + \left( { - 1, - \frac{1}{2},0} \right) + \left( {6, - 9, - 15} \right)\).
Tọa độ của \(\vec x\) là:
\(x = - 2 - 1 + 6 = 3,y = 0 - \frac{1}{2} - 9 = - \frac{{19}}{2},z = 6 + 0 - 15 = - 9.\)
Vậy, tọa độ của vectơ \(\vec x\) là \(\left( {3, - \frac{{19}}{2}, - 9} \right)\).
Trả lời câu hỏi Hoạt động 4 trang 71 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hai điểm \(M({x_M},{y_M},{z_M})\) và \(N({x_N},{y_N},{z_N})\) (Hình 2.36).
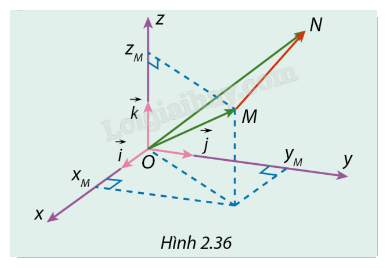
a) Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \).
b) Biểu diễn mỗi vectơ \(\overrightarrow {OM} \), \(\overrightarrow {ON} \) qua các vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\).
c) Chứng minh rằng \(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\).
Phương pháp giải:
- Sử dụng định nghĩa và tính chất của vectơ trong không gian.
- Sử dụng biểu thức của vectơ trong hệ tọa độ Oxyz qua các vectơ đơn vị \(\vec i\), \(\vec j\),\(\vec k\).
Lời giải chi tiết:
a) Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \):
Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \)
b) Biểu diễn mỗi vectơ \(\overrightarrow {OM} \), \(\overrightarrow {ON} \) qua các vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\):
Với các tọa độ đã cho:
\(\overrightarrow {OM} = {x_M}\vec i + {y_M}\vec j + {z_M}\vec k\)
\(\overrightarrow {ON} = {x_N}\vec i + {y_N}\vec j + {z_N}\vec k\)
c) Chứng minh rằng \(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\):
Dùng kết quả của phần (a) và (b): \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = ({x_N}\vec i + {y_N}\vec j + {z_N}\vec k) - ({x_M}\vec i + {y_M}\vec j + {z_M}\vec k)\)
Kết quả:
\(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\)
Trả lời câu hỏi Luyện tập 5 trang 72 SGK Toán 12 Cùng khám phá
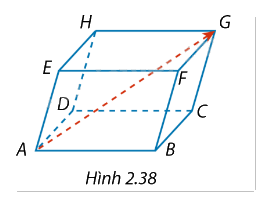
Trong không gian Oxyz, cho hình hộp ABCD.EFGH có A(1; 0; -1), B(2; 1; 3) và H(4; 3; 4) (Hình 2.38).
a) Tìm tọa độ của đỉnh G.
b) Tìm tọa độ của \(\overrightarrow {AG} \).
Phương pháp giải:
- Sử dụng các tính chất của hình hộp chữ nhật trong không gian, đặc biệt là các quy tắc liên quan đến tọa độ của các đỉnh dựa trên tính chất đối xứng và các đường chéo.
- Áp dụng công thức sau để tính toạ độ vectơ trong không gian.
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A}} \right)\)
Lời giải chi tiết:
a) Tìm toạ độ của điểm G
Vì ABCD.EFGH là một hình hộp, nên G là đỉnh đối diện với A và \(\overrightarrow {HG} = \overrightarrow {AB} \).
Mà \(\overrightarrow {HG} = \overrightarrow {OG} - \overrightarrow {OH} \) nên suy ra \(\overrightarrow {OG} = \overrightarrow {AB} + \overrightarrow {OH} \)
Do đó, tọa độ của G được tính bằng cách lấy toạ độ của vectơ \(\overrightarrow {AB} \) cộng tọa độ của điểm H hay nói cách khác là lấy toạ độ của điểm B cộng với tọa độ của điểm H trừ đi tọa độ của điểm A: \(G = B + H - A\)
Tính toán cụ thể: \(G = (2,1,3) + (4,3,4) - (1,0, - 1) = (5,4,8)\)
Vậy tọa độ của điểm \(G\) là \((5,4,8)\).
b) Tìm tọa độ của \(\overrightarrow {AG} \):
Tọa độ của vectơ \(\overrightarrow {AG} \) được tính bằng tọa độ của G trừ tọa độ của A:
\(\overrightarrow {AG} = ({x_G} - {x_A},{y_G} - {y_A},{z_G} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AG} = (5 - 1,4 - 0,8 - ( - 1)) = (4,4,9)\)
Vậy tọa độ của \(\overrightarrow {AG} \) là \((4,4,9)\).
Trả lời câu hỏi Vận dụng trang 72 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz,\),một vật đi từ điểm \(A(2;3;0)\) đến điểm \(B( - 1;1;2)\) rồi tiếp tục đi đến điểm \(C(3; - 2; - 1)\). Tìm vectơ biểu thị độ dịch chuyển của vật khi:
a) Vật đi từ điểm \(A\) đến điểm \(B\);
b) Vật đi từ điểm \(A\) đến điểm \(C\).
Phương pháp giải:
- Để tìm vectơ biểu thị độ dịch chuyển của vật, ta sử dụng công thức tính vectơ từ một điểm này đến một điểm khác trong không gian ba chiều.
- Vectơ độ dịch chuyển từ điểm \(A\) đến điểm \(B\) được tính bằng tọa độ điểm \(B\) trừ đi tọa độ điểm \(A\).
- Tương tự, vectơ độ dịch chuyển từ điểm \(A\) đến điểm \(C\) được tính bằng tọa độ điểm \(C\) trừ đi tọa độ điểm \(A\).
Lời giải chi tiết:
a) Vectơ độ dịch chuyển của vật khi đi từ \(A\) đến \(B\):
Vectơ \(\overrightarrow {AB} \) được tính bằng công thức:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AB} = ( - 1 - 2;1 - 3;2 - 0) = ( - 3; - 2;2)\)
Vậy vectơ độ dịch chuyển từ \(A\) đến \(B\) là \(\overrightarrow {AB} = ( - 3; - 2;2)\).
b) Vectơ độ dịch chuyển của vật khi đi từ \(A\) đến \(C\):
Vectơ \(\overrightarrow {AC} \) được tính bằng công thức:
\(\overrightarrow {AC} = ({x_C} - {x_A};{y_C} - {y_A};{z_C} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AC}= (3 - 2; - 2 - 3; - 1 - 0) = (1; - 5; - 1)\)
Vậy vectơ độ dịch chuyển từ \(A\) đến \(C\) là \(\overrightarrow {AC} = (1; - 5; - 1)\).
Giải mục 3 trang 70, 71, 72 SGK Toán 12 tập 1: Tổng quan và Phương pháp giải
Mục 3 trong SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các dạng bài tập về tính đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, và giải các bài toán liên quan đến đạo hàm. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Nội dung chi tiết Giải mục 3 trang 70, 71, 72
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 3, chúng ta sẽ đi vào phân tích chi tiết từng bài tập cụ thể:
Bài 1: Tính đạo hàm của hàm số
Bài tập này yêu cầu các em vận dụng các quy tắc tính đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, và quy tắc đạo hàm của hàm hợp. Ví dụ:
Cho hàm số y = x3 + 2x2 - 5x + 1. Tính đạo hàm y’.
Lời giải:
y’ = 3x2 + 4x - 5
Bài 2: Khảo sát hàm số bằng đạo hàm
Bài tập này yêu cầu các em sử dụng đạo hàm để xác định các điểm cực trị, khoảng đồng biến, nghịch biến, và vẽ đồ thị hàm số. Ví dụ:
Khảo sát hàm số y = x3 - 3x2 + 2.
Lời giải:
- Tính đạo hàm y’ = 3x2 - 6x
- Giải phương trình y’ = 0 để tìm các điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến và các điểm cực trị.
- Vẽ đồ thị hàm số.
Bài 3: Ứng dụng đạo hàm để giải các bài toán thực tế
Bài tập này yêu cầu các em vận dụng kiến thức về đạo hàm để giải các bài toán liên quan đến vận tốc, gia tốc, tối ưu hóa, và các bài toán thực tế khác. Ví dụ:
Một vật chuyển động với vận tốc v(t) = 3t2 - 6t + 2 (m/s). Tính gia tốc của vật tại thời điểm t = 1s.
Lời giải:
Gia tốc a(t) = v’(t) = 6t - 6. Tại t = 1s, a(1) = 6(1) - 6 = 0 (m/s2).
Phương pháp giải bài tập hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, các em cần:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Hiểu rõ các ứng dụng của đạo hàm trong việc khảo sát hàm số và giải các bài toán thực tế.
- Luyện tập thường xuyên để rèn luyện kỹ năng và tư duy.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra kết quả.
Tại sao nên chọn tusach.vn để học Toán 12?
tusach.vn cung cấp:
- Lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1.
- Đội ngũ giáo viên giàu kinh nghiệm, nhiệt tình hỗ trợ.
- Giao diện thân thiện, dễ sử dụng.
- Cập nhật kiến thức mới nhất.
Hãy truy cập tusach.vn ngay hôm nay để học Toán 12 hiệu quả và đạt kết quả cao!