Lý thuyết Tích phân Toán 12 Cùng khám phá
Tổng quan nội dung
Lý Thuyết Tích Phân Toán 12: Nền Tảng Quan Trọng
Tích phân là một trong những khái niệm cốt lõi của giải tích, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật.
Trong chương trình Toán 12, việc nắm vững lý thuyết tích phân là điều kiện cần thiết để giải quyết các bài toán phức tạp và đạt kết quả cao trong kỳ thi THPT Quốc gia.
tusach.vn xin giới thiệu tài liệu Lý thuyết Tích phân Toán 12, được trình bày một cách dễ hiểu, logic và đầy đủ.
1. Khái niệm tích phân Một số bài toán dẫn đến khái niệm tích phân a) Quãng đường đi được của một vật
1. Khái niệm tích phân
Một số bài toán dẫn đến khái niệm tích phân
a) Quãng đường đi được của một vật
Xét một vật chuyển động thẳng với vận tốc v = v(t) (0 < t < T) và không đổi chiều chuyển động. Gọi F(t) là một nguyên hàm bất kỳ của v(t) trên khoảng (0;T) thì quãng đường vật đi được từ thời điểm t = a đến thời điểm t = b là L = F(b) − F(a) với 0 < a < b < T.
b) Diện tích hình thang cong
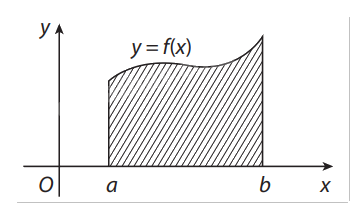
Cho hàm số f(x) liên tục trên đoạn [a;b]. Hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x = a, x = bđược gọi là hình thang cong.
Trong trường hợp tổng quát, cho hàm số y = f(x) liên tục, không âm trên đoạn [a;b], người ta chứng minh được rằng diện tích hình thang cong giới hạn bởi đồ thị hàm số y=f(x), trục hoành và các đường thẳng x = a, x = b bằng F(b) − F(a), với F(x) là một nguyên hàm của f(x) trên đoạn [a;b].
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(f(x) = {x^2} + 1\) và các đường thẳng x = -1, x = 2.
Định nghĩa tích phân
| Cho hàm số f(x) liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\) thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là \(\int\limits_a^b {f(x)dx} \). |
Ta còn dùng ký hiệu F(x) để chỉ hiệu số F(b) − F(a).
Vậy \(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}b\\a\end{array}} \right. = F(b) - F(a)\).
Ta gọi \(\int\limits_a^b {} \) là dấu tích phân, a là cận dưới, b là cận trên, \(f\left( x \right)dx\) là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.
Ghi chú:
- Quy ước: \(\int\limits_a^0 {f(x)dx} = 0\), nếu b > a thì \(\int\limits_b^a {f(x)dx} = - \int\limits_a^b {f(x)dx} \).
- Tích phân chỉ phụ thuộc vào hàm số dưới dấu tích phân và các cận a, b mà không phụ thuộc vào biến x hay t, nghĩa là \(\int\limits_a^b {f(x)dx} = \int\limits_a^b {f(t)dt} \).
- Ý nghĩa hình học của tích phân: Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a;b] thì diện tích S của hình thang cong (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = a, x = blà \(S = \int\limits_a^b {f(x)dx} \).
Ví dụ:
a) \(\int\limits_2^3 {3{x^2}dx} = {x^3}\left| {\begin{array}{*{20}{c}}3\\2\end{array}} \right. = {3^3} - {2^3} = 27 - 8 = 19\).
b) \(\int\limits_2^3 {{e^t}dt} = {e^t}\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right. = {e^1} - {e^0} = e - 1\).
2. Tính chất của tích phân
+ \(\int\limits_a^b {kf(x)dx = k\int\limits_a^b {f(x)dx} } \) (k là hằng số) + \(\int\limits_a^b {\left[ {f(x) + g(x)} \right]} dx = \int\limits_a^b {f(x)dx + \int\limits_a^b {g(x)dx} } \) + \(\int\limits_a^b {\left[ {f(x) - g(x)} \right]} dx = \int\limits_a^b {f(x)dx - \int\limits_a^b {g(x)dx} } \) + \(\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx + \int\limits_c^b {f(x)dx} } } \) (a < c < b) |
Ví dụ:
a) Cho \(\int\limits_0^2 {\sqrt {{e^x}} dx} = 2(e - 1)\). Tính \(\int\limits_0^2 {\frac{{\sqrt {{e^x}} }}{2}dx} \).
Ta có \(\int\limits_0^2 {\frac{{\sqrt {{e^x}} }}{2}dx} = \frac{1}{2}\int\limits_0^2 {\sqrt {{e^x}} dx} = \frac{1}{2}.2(e - 1) = e - 1\).
b) Tính \(\int\limits_0^{\frac{\pi }{2}} {(3\sin x - \cos x)dx} \).
\(\int\limits_0^{\frac{\pi }{2}} {(3\sin x - \cos x)dx} = 3\int\limits_0^{\frac{\pi }{2}} {\sin xdx} - \int\limits_0^{\frac{\pi }{2}} {\cos xdx} \)
\( = ( - 3\cos x)\left| {\begin{array}{*{20}{c}}{\frac{\pi }{2}}\\0\end{array}} \right. - \sin \left| {\begin{array}{*{20}{c}}{\frac{\pi }{2}}\\0\end{array}} \right. = - 3(0 - 1) - (1 - 0) = 2\).
c) Cho các hàm số f(x), g(x) liên tục trên đoạn [1;3] và \(\int\limits_1^2 {f(x)dx} = \frac{1}{2}\), \(\int\limits_2^3 {f(x)dx} = \frac{3}{2}\), \(\int\limits_1^3 {g(x)dx} = - 1\).
Ta có:
\(\int\limits_1^3 {f(x)dx} = \int\limits_1^2 {f(x)dx} + \int\limits_2^3 {f(x)dx} = \frac{1}{2} + \frac{3}{2} = 2\).
\(\int\limits_1^3 {[2f(x) + g(x)]dx} = 2\int\limits_1^3 {f(x)dx} + \int\limits_1^3 {f(x)dx} = 2.2 - 1 = 3\).
3. Tính tích phân trong một số trường hợp đơn giản
a) \(\int\limits_1^2 {{{(2x - 3)}^2}dx} = \int\limits_1^2 {(4{x^2} - 12x + 9)dx} = 4\int\limits_1^2 {{x^2}dx} - 12\int\limits_1^2 {xdx} + \int\limits_1^2 {9dx} \)
\( = \left( {\frac{4}{3}{x^3}} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. - \left( {6{x^2}} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. + (9x)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. = \frac{1}{3}\).
b) \(\int\limits_{ - 1}^0 {{5^{2x - 1}}dx} = \frac{1}{5}\int\limits_{ - 1}^0 {{5^{2x}}dx} = \frac{1}{5}\int\limits_{ - 1}^0 {{{25}^x}dx} = \frac{{{{25}^x}}}{{5\ln 25}}\left| {\begin{array}{*{20}{c}}0\\{ - 1}\end{array}} \right. = \frac{{24}}{{125\ln 25}}\).
c) \(\int\limits_{ - \frac{\pi }{4}}^0 {(2{{\tan }^2}x + 5)dx} = \int\limits_{ - \frac{\pi }{4}}^0 {\left[ {2(1 + {{\tan }^2}x) + 3} \right]dx} = 2\int\limits_{ - \frac{\pi }{4}}^0 {\frac{1}{{{{\cos }^2}x}}dx} + \int\limits_{ - \frac{\pi }{4}}^0 {3dx} \)
\( = 2(\tan x)\left| {\begin{array}{*{20}{c}}0\\{ - \frac{\pi }{4}}\end{array} + (3x)} \right.\left| {\begin{array}{*{20}{c}}0\\{ - \frac{\pi }{4}}\end{array}} \right. = \frac{{3\pi + 8}}{4}\).
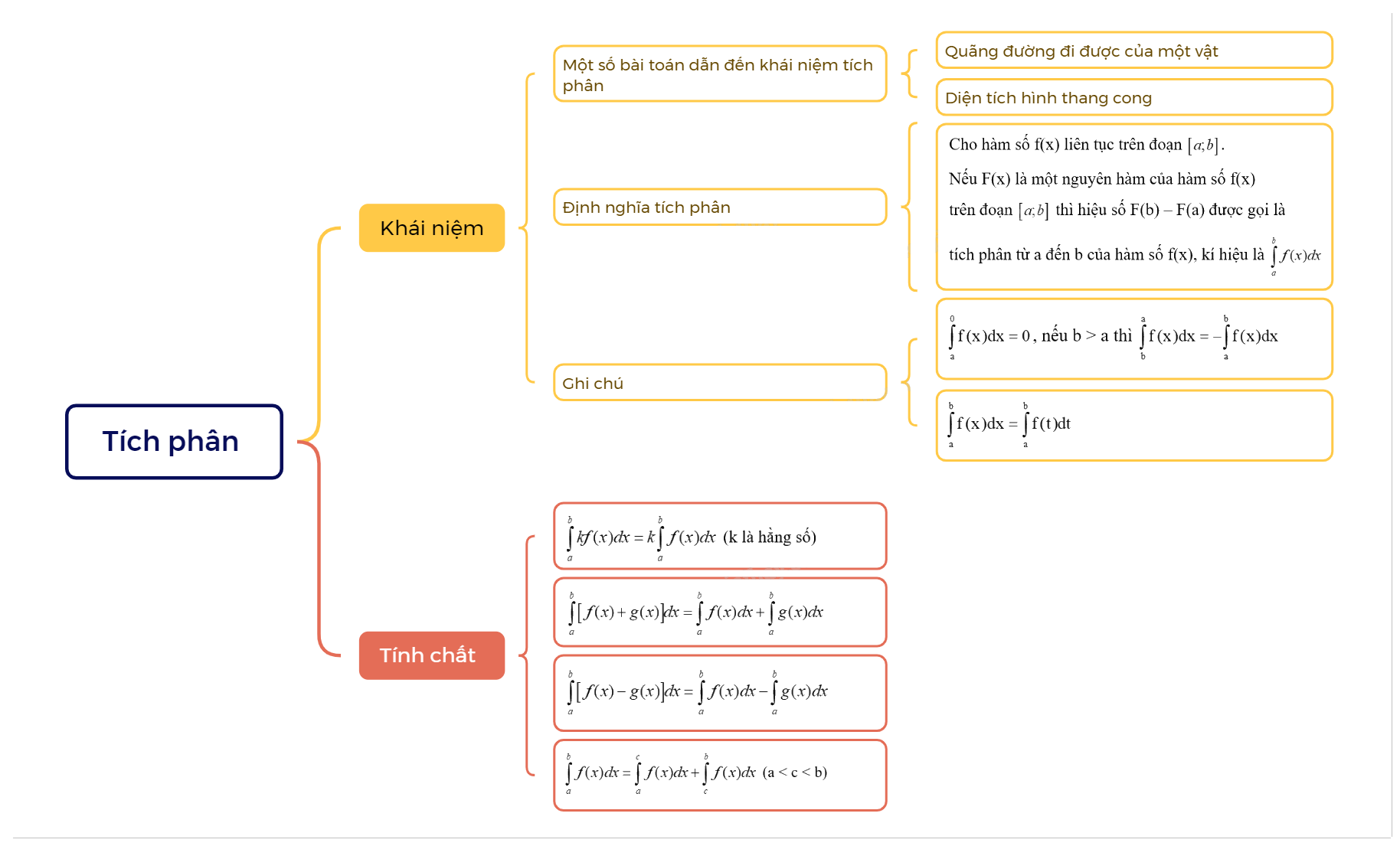
Lý Thuyết Tích Phân Toán 12: Tổng Quan
Tích phân, cùng với đạo hàm, là hai khái niệm nền tảng của giải tích. Về cơ bản, tích phân là quá trình ngược lại của đạo hàm. Trong khi đạo hàm cho biết tốc độ thay đổi của một hàm số, tích phân cho biết sự tích lũy của một hàm số theo một biến số.
1. Nguyên Hàm của Một Hàm Số
Nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x), tức là F'(x) = f(x). Nguyên hàm không duy nhất, vì nếu F(x) là một nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x), với C là một hằng số bất kỳ.
Công thức tính nguyên hàm cơ bản:
- ∫xn dx = (xn+1)/(n+1) + C (với n ≠ -1)
- ∫1/x dx = ln|x| + C
- ∫ex dx = ex + C
- ∫sin(x) dx = -cos(x) + C
- ∫cos(x) dx = sin(x) + C
2. Tích Phân Xác Định và Tích Phân Bất Định
Tích phân bất định là việc tìm nguyên hàm của một hàm số. Kết quả của tích phân bất định là một họ các hàm số khác nhau bởi một hằng số.
Tích phân xác định là việc tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số f(x), trục hoành và hai đường thẳng x = a và x = b. Ký hiệu: ∫ab f(x) dx
Định lý cơ bản của tích phân: ∫ab f(x) dx = F(b) - F(a), trong đó F(x) là một nguyên hàm của f(x).
3. Các Phương Pháp Tính Tích Phân
Có nhiều phương pháp để tính tích phân, tùy thuộc vào dạng của hàm số:
- Phương pháp đổi biến số: Sử dụng để đơn giản hóa tích phân bằng cách thay đổi biến số.
- Phương pháp tích phân từng phần: Sử dụng để tính tích phân của tích hai hàm số. Công thức: ∫u dv = uv - ∫v du
- Phương pháp phân tích thành phân thức đơn giản: Sử dụng để tính tích phân của các hàm số hữu tỉ.
4. Ứng Dụng của Tích Phân
Tích phân có rất nhiều ứng dụng trong thực tế, bao gồm:
- Tính diện tích hình phẳng: Như đã đề cập ở trên.
- Tính thể tích vật thể: Sử dụng tích phân để tính thể tích của các vật thể có hình dạng phức tạp.
- Tính độ dài đường cong: Sử dụng tích phân để tính độ dài của một đường cong.
- Tính công thực hiện bởi một lực: Sử dụng tích phân để tính công thực hiện bởi một lực thay đổi theo vị trí.
Ví Dụ Minh Họa
Ví dụ 1: Tính ∫x2 dx
Giải: ∫x2 dx = (x3)/3 + C
Ví dụ 2: Tính ∫01 x dx
Giải: ∫01 x dx = [x2/2]01 = (12/2) - (02/2) = 1/2
Lời Khuyên Khi Học Lý Thuyết Tích Phân
- Nắm vững các công thức nguyên hàm cơ bản.
- Luyện tập thường xuyên các bài tập về tích phân.
- Hiểu rõ các phương pháp tính tích phân và biết khi nào nên sử dụng phương pháp nào.
- Áp dụng kiến thức tích phân vào giải quyết các bài toán thực tế.
Hy vọng tài liệu Lý thuyết Tích phân Toán 12 này sẽ giúp bạn học tập hiệu quả và đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!