Giải mục 1 trang 72, 73 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 72, 73 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 72, 73 sách giáo khoa Toán 12 tập 2. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những tài liệu và lời giải chính xác, dễ hiểu nhất.
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.
LT1
Trả lời câu hỏi Luyện tập 1 trang 73 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt cầu (S) đi qua gốc toạ độ O, bán kính r = 5. Tìm toạ độ tâm I của (S), biết điểm I thuộc đường thẳng
\(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = t}\\{z = 4 + 2t}\end{array}} \right.\quad (t \in \mathbb{R}).\)
Phương pháp giải:
Gọi \(I(a,b,c)\) là tọa độ của tâm mặt cầu \(S\).
Vì mặt cầu \(S\) đi qua gốc tọa độ \(O(0,0,0)\), nên \(IO = r = 5\).
Đặt \(I\) nằm trên đường thẳng \(d\) và tìm giá trị \(t\) sao cho khoảng cách \(IO = 5\).
Giải phương trình để tìm \(t\), từ đó xác định tọa độ của \(I\).
Lời giải chi tiết:
Giả sử \(I(a,b,c)\) có tọa độ: \(a = 3 - t, b = t, c = 4 + 2t.\)
Do \(IO = 5\), ta có: \(IO = \sqrt {{a^2} + {b^2} + {c^2}} = 5.\)
Thay \(a = 3 - t\), \(b = t\), \(c = 4 + 2t\) vào phương trình:
\(\begin{array}{l}\sqrt {{{(3 - t)}^2} + {t^2} + {{(4 + 2t)}^2}} = 5.\\ \Leftrightarrow 9 - 6t + {t^2} + {t^2} + 16 + 16t + 4{t^2} = 25\\ \Leftrightarrow 6{t^2} + 10t + 25 = 25\\ \Leftrightarrow 2t(3t + 5) = 0\\ \Leftrightarrow t = 0,\,\,\,t = - \frac{5}{3}\end{array}\)
Vậy có hai toạ độ tâm I thoả mãn là \(I(3;0;4)\) hoặc \(I\left( {\frac{{14}}{3}; - \frac{5}{3};\frac{2}{3}} \right)\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 72 SGK Toán 12 Cùng khám phá
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.
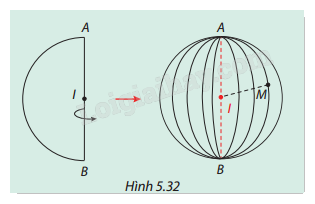
Phương pháp giải:
Khoảng cách từ tâm nửa đường tròn tới bất kỳ điểm nào nằm trên nửa đường tròn đều bằng nhau.
Lời giải chi tiết:
Vì M là vị trí của một điểm thuộc nửa đường tròn quay quanh AB, nên điểm M luôn có cùng khoảng cách từ I đến điểm đó như khoảng cách từ I đến bất kỳ điểm nào trên nửa đường tròn ban đầu, tức là IM = r.
Do bán kính không thay đổi trong suốt quá trình quay, khoảng cách từ I đến M vẫn giữ nguyên giá trị là 𝑟.
- HĐ1
- LT1
Trả lời câu hỏi Hoạt động 1 trang 72 SGK Toán 12 Cùng khám phá
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.
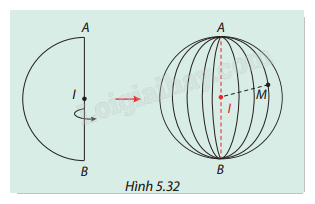
Phương pháp giải:
Khoảng cách từ tâm nửa đường tròn tới bất kỳ điểm nào nằm trên nửa đường tròn đều bằng nhau.
Lời giải chi tiết:
Vì M là vị trí của một điểm thuộc nửa đường tròn quay quanh AB, nên điểm M luôn có cùng khoảng cách từ I đến điểm đó như khoảng cách từ I đến bất kỳ điểm nào trên nửa đường tròn ban đầu, tức là IM = r.
Do bán kính không thay đổi trong suốt quá trình quay, khoảng cách từ I đến M vẫn giữ nguyên giá trị là 𝑟.
Trả lời câu hỏi Luyện tập 1 trang 73 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt cầu (S) đi qua gốc toạ độ O, bán kính r = 5. Tìm toạ độ tâm I của (S), biết điểm I thuộc đường thẳng
\(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = t}\\{z = 4 + 2t}\end{array}} \right.\quad (t \in \mathbb{R}).\)
Phương pháp giải:
Gọi \(I(a,b,c)\) là tọa độ của tâm mặt cầu \(S\).
Vì mặt cầu \(S\) đi qua gốc tọa độ \(O(0,0,0)\), nên \(IO = r = 5\).
Đặt \(I\) nằm trên đường thẳng \(d\) và tìm giá trị \(t\) sao cho khoảng cách \(IO = 5\).
Giải phương trình để tìm \(t\), từ đó xác định tọa độ của \(I\).
Lời giải chi tiết:
Giả sử \(I(a,b,c)\) có tọa độ: \(a = 3 - t, b = t, c = 4 + 2t.\)
Do \(IO = 5\), ta có: \(IO = \sqrt {{a^2} + {b^2} + {c^2}} = 5.\)
Thay \(a = 3 - t\), \(b = t\), \(c = 4 + 2t\) vào phương trình:
\(\begin{array}{l}\sqrt {{{(3 - t)}^2} + {t^2} + {{(4 + 2t)}^2}} = 5.\\ \Leftrightarrow 9 - 6t + {t^2} + {t^2} + 16 + 16t + 4{t^2} = 25\\ \Leftrightarrow 6{t^2} + 10t + 25 = 25\\ \Leftrightarrow 2t(3t + 5) = 0\\ \Leftrightarrow t = 0,\,\,\,t = - \frac{5}{3}\end{array}\)
Vậy có hai toạ độ tâm I thoả mãn là \(I(3;0;4)\) hoặc \(I\left( {\frac{{14}}{3}; - \frac{5}{3};\frac{2}{3}} \right)\).
Giải mục 1 trang 72, 73 SGK Toán 12 tập 2: Tổng quan và Phương pháp giải
Mục 1 trang 72, 73 SGK Toán 12 tập 2 thường xoay quanh các chủ đề về Đạo hàm của hàm số lượng giác. Đây là một phần quan trọng trong chương trình Toán 12, đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng áp dụng chúng vào giải bài tập.
Nội dung chính của Mục 1 trang 72, 73
- Công thức đạo hàm của các hàm số lượng giác cơ bản: sin(x), cos(x), tan(x), cot(x).
- Quy tắc đạo hàm của hàm hợp: Áp dụng quy tắc chuỗi để tính đạo hàm của các hàm số phức tạp.
- Bài tập vận dụng: Giải các bài tập liên quan đến việc tính đạo hàm của hàm số lượng giác và hàm hợp.
Công thức đạo hàm cần nhớ
| Hàm số | Đạo hàm |
|---|---|
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | 1/cos2(x) |
| cot(x) | -1/sin2(x) |
Phương pháp giải bài tập
- Xác định hàm số cần đạo hàm: Đọc kỹ đề bài để xác định chính xác hàm số cần tính đạo hàm.
- Áp dụng công thức đạo hàm: Sử dụng các công thức đạo hàm đã học để tính đạo hàm của hàm số.
- Rút gọn biểu thức: Rút gọn biểu thức đạo hàm để có kết quả cuối cùng.
- Kiểm tra lại kết quả: Kiểm tra lại kết quả để đảm bảo tính chính xác.
Ví dụ minh họa
Bài tập: Tính đạo hàm của hàm số y = sin(2x + 1).
Giải:
Sử dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x + 1) * (2x + 1)' = 2cos(2x + 1)
Lưu ý quan trọng
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
tusach.vn hy vọng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải các bài tập về đạo hàm của hàm số lượng giác. Chúc các em học tập tốt!
Các bài tập tương tự
Các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 2 và các tài liệu ôn thi THPT Quốc gia để củng cố kiến thức.