Giải bài tập 3.11 trang 104 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 3.11 Trang 104 Toán 12 Tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3.11 trang 104 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Một trang trại phân 1000 quả trứng thành 5 loại, tuỳ theo khối lượng (đã được làm tròn) của chúng (Bảng 3.26).
Đề bài
Một trang trại phân 1000 quả trứng thành 5 loại, tuỳ theo khối lượng (đã được làm tròn) của chúng (Bảng 3.26).
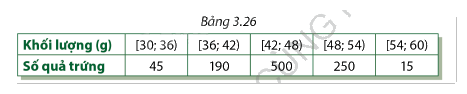
a) Ước tính khoảng biến thiên, khoảng tứ phân vị, phương sai và độ lệch chuẩn của khối lượng những quả trứng này (làm tròn kết quả đến hàng phần trăm).
b) Hãy phân tích sự đồng đều về khối lượng các quả trứng của trang trại.
Phương pháp giải - Xem chi tiết
a) Áp dụng các công thức sau:
- Khoảng biến thiên là sự chênh lệch giữa giá trị lớn nhất và nhỏ nhất trong tập dữ liệu.
- Khoảng tứ phân vị là khoảng giữa \({Q_3}\) và \({Q_1}\), ký hiệu là:\({\Delta _Q} = {Q_3} - {Q_1}\) với công thức tính tứ phân vị là:
\({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
- Công thức tính trung bình là:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
- Công thức tính phương sai:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
b)
Khoảng biến thiên (R): Nếu khoảng biến thiên nhỏ, điều đó cho thấy sự khác biệt về khối lượng giữa quả trứng lớn nhất và nhỏ nhất là nhỏ, tức là các quả trứng có khối lượng khá đồng đều.
Khoảng tứ phân vị (\({\Delta _Q}\)): \({\Delta _Q}\) nhỏ cho thấy 50% giữa của các quả trứng có khối lượng gần nhau, điều này cũng chỉ ra sự đồng đều về khối lượng.
Phương sai và độ lệch chuẩn: Phương sai và độ lệch chuẩn nhỏ cho thấy các giá trị khối lượng của quả trứng không phân tán nhiều so với giá trị trung bình, nghĩa là khối lượng các quả trứng khá đồng đều.
Lời giải chi tiết
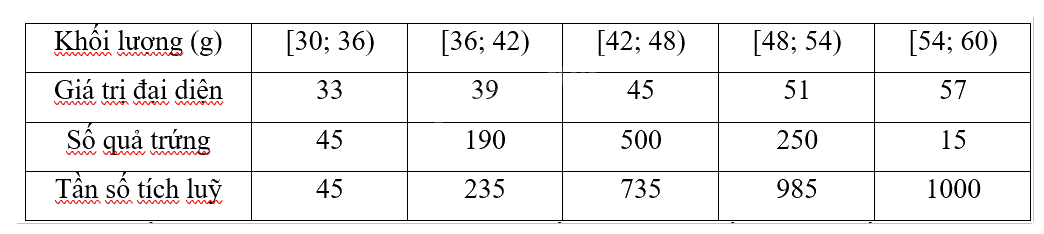
Khoảng biến thiên là chênh lệch giữa giá trị khối lượng lớn nhất và nhỏ nhất:
R = Giá trị lớn nhất – Giá trị nhỏ nhất = 60 – 30 = 30
Tính tứ phân vị
- \(\frac{N}{4} = 250\) rơi vào nhóm [42; 48)
\({Q_1} = 42 + \left( {\frac{{250 - 235}}{{500}}} \right) \times 6\)
\({Q_1} = 42 + \left( {\frac{{15}}{{500}}} \right) \times 6 = 42 + 0,18 = 42,18{\mkern 1mu} {\rm{g}}\)
- \(\frac{{3N}}{4} = 750\) rơi vào nhóm [48; 54)
\({Q_3} = 48 + \left( {\frac{{750 - 735}}{{250}}} \right) \times 6\)
\({Q_3} = 48 + \left( {\frac{{15}}{{250}}} \right) \times 6 = 48 + 0,36 = 48,36{\mkern 1mu} {\rm{g}}\)
Khoảng tứ phân vị:
\({\Delta _Q} = {Q_3} - {Q_1} = 48,36 - 42,18 = 6,18{\mkern 1mu} {\rm{g}}\)
Giá trị trung bình:
\(\overline x = \frac{{(33 \times 45) + (39 \times 190) + (45 \times 500) + (51 \times 250) + (57 \times 15)}}{{1000}}\)
\(\overline x = \frac{{1485 + 7410 + 22500 + 12750 + 855}}{{1000}} = \frac{{45000}}{{1000}} = 45{\mkern 1mu} {\rm{g}}\)
Phương sai:
\({S^2} = \frac{{45 \times {{(33 - 45)}^2} + 190 \times {{(39 - 45)}^2} + 500 \times {{(45 - 45)}^2} + 250 \times {{(51 - 45)}^2} + 15 \times {{(57 - 45)}^2}}}{{1000}}\)
\({S^2} = \frac{{45 \times 144 + 190 \times 36 + 500 \times 0 + 250 \times 36 + 15 \times 144}}{{1000}}\)
\({S^2} = \frac{{6480 + 6840 + 0 + 9000 + 2160}}{{1000}} = \frac{{24,480}}{{1000}} = 24,48{\mkern 1mu} {{\rm{g}}^2}\)
Độ lệch chuẩn của khối lượng những quả trứng này:
\(S = \sqrt {{S^2}} = \sqrt {24,48} \approx 4,95g\)
b)
Khoảng biến thiên: 30g cho thấy sự khác biệt lớn giữa quả trứng nhẹ nhất và nặng nhất, nhưng điều này không phản ánh toàn bộ sự đồng đều của dữ liệu.
Khoảng tứ phân vị: 6.18g, cho thấy rằng 50% quả trứng giữa có khối lượng rất gần nhau, trong khoảng từ 42.18g đến 48.36g. Điều này cho thấy sự phân tán không quá lớn trong số lượng lớn các quả trứng.
Phương sai và độ lệch chuẩn: Với phương sai là 24,48g và độ lệch chuẩn là 4,95g, có thể thấy rằng có một số sự phân tán trong khối lượng trứng, nhưng không quá lớn, cho thấy khối lượng các quả trứng trong trang trại là khá đồng đều.
Giải Bài Tập 3.11 Trang 104 Toán 12 Tập 1: Chi Tiết và Dễ Hiểu
Bài tập 3.11 trang 104 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
- Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
- Tính đạo hàm bậc nhất: Tính f'(x) để tìm các điểm dừng (điểm mà f'(x) = 0 hoặc không xác định).
- Lập bảng biến thiên: Xác định dấu của f'(x) trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến.
- Tìm cực trị: Sử dụng dấu của f'(x) để xác định điểm cực đại, cực tiểu.
- Khảo sát giới hạn và tiệm cận: Xác định giới hạn của hàm số khi x tiến tới vô cùng và các điểm không xác định.
- Vẽ đồ thị hàm số: Dựa trên các thông tin đã thu thập để vẽ đồ thị hàm số.
Lời Giải Chi Tiết Bài Tập 3.11
Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể. Giả sử hàm số cần khảo sát là:
f(x) = x3 - 3x2 + 2
Bước 1: Tập xác định
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
Bước 2: Tính đạo hàm bậc nhất
f'(x) = 3x2 - 6x
Bước 3: Tìm điểm dừng
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm dừng.
Bước 4: Lập bảng biến thiên
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Bước 5: Tìm cực trị
- Tại x = 0, f'(x) đổi dấu từ dương sang âm, do đó hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2.
- Tại x = 2, f'(x) đổi dấu từ âm sang dương, do đó hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = -2.
Kết luận
Hàm số f(x) = x3 - 3x2 + 2 đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2). Hàm số đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 3.11 trang 104 SGK Toán 12 tập 1. Hãy luyện tập thêm nhiều bài tập khác để nâng cao kỹ năng giải toán của mình nhé!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi trong phần bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ các em.