Giải bài tập 1.39 trang 47 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 1.39 Trang 47 SGK Toán 12 Tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.39 trang 47 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
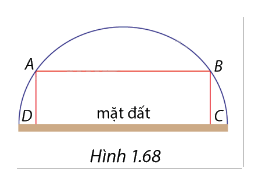
Một cổng vòm có dạng nửa hình tròn trên mặt đất với bán kính R=5 m. Người ta muốn đặt một khung hình chữ nhật ABCD để thiết kế trang trí, với hai điểm A,B đính trên vòm và CD đặt trên mặt đất (Hình 1.68). Tìm khoảng cách A,B so với mặt đất để diện tích hình chữ nhật ABCD là lớn nhất.
Đề bài
Một cổng vòm có dạng nửa hình tròn trên mặt đất với bán kính R=5 m. Người ta muốn đặt một khung hình chữ nhật ABCD để thiết kế trang trí, với hai điểm A,B đính trên vòm và CD đặt trên mặt đất (Hình 1.68). Tìm khoảng cách A,B so với mặt đất để diện tích hình chữ nhật ABCD là lớn nhất.
Phương pháp giải - Xem chi tiết
- Đặt y (m) là khoảng cách từ AB đến mặt đất. Vì A và B nằm trên vòm nửa hình tròn có bán kính R=5 m, nên tọa độ của A và B có thể biểu diễn dưới dạng (x,y).
- Tìm phương trình đường tròn và tính diện tích S của hình chữ nhật ABCD.
- Biểu diễn S dưới dạng một hàm của y và cực đại hóa S bằng cách tìm đạo hàm.
Lời giải chi tiết
Gọi y (m) là khoảng cách từ A và B đến mặt đất (y>0).
Vì A và B nằm trên nửa hình tròn có tâm tại gốc tọa độ (0,0) và bán kính R=5 m, tọa độ của chúng thỏa mãn phương trình đường tròn:
\({x^2} + {y^2} = 25\)
Giả sử A có toạ độ \(( - x,y)\) và B có toạ độ \((x,y)\).
Chiều dài AB là: \(\sqrt {{{( - x - x)}^2} + {{(y - y)}^2}} = 2x\)
Diện tích hình chữ nhật ABCD là: \(S = AB.AD = 2xy\)
Thay \(x = \sqrt {25 - {y^2}} \) vào biểu thức diện tích ta được: \(S = 2\sqrt {25 - {y^2}} .y\)
Đạo hàm của S theo y: \(\)\(S' = 2\left( {\sqrt {25 - {y^2}} + y.\frac{{ - y}}{{\sqrt {25 - {y^2}} }}} \right) = 2\left( {\frac{{25 - {y^2} - {y^2}}}{{\sqrt {25 - {y^2}} }}} \right) = 2\left( {\frac{{25 - 2{y^2}}}{{\sqrt {25 - {y^2}} }}} \right)\)
Đặt đạo hàm bằng 0, ta có: \(S' = 0 \Leftrightarrow 25 - 2{y^2} = 0 \Leftrightarrow 2{y^2} = 25 \Rightarrow y = \frac{{5\sqrt 2 }}{2}\)
Đạo hàm cấp 2 của S:
\(\begin{array}{l}S'' = 2.\frac{{ - 4y.\sqrt {25 - {y^2}} + (25 - 2{y^2})\frac{y}{{\sqrt {25 - {y^2}} }}}}{{25 - {y^2}}}\\ = 2.\frac{{ - 4y\sqrt {25 - {y^2}} + \frac{{y\left( {25 - 2{y^2}} \right)}}{{\sqrt {25 - {y^2}} }}}}{{25 - {y^2}}}\\ = 2.\frac{{ - 4y\left( {25 - {y^2}} \right) + y\left( {25 - 2{y^2}} \right)}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 4y\left( {25 - {y^2}} \right) + y\left( {25 - 2{y^2}} \right)}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 100y + 4{y^3} + 25y - 2{y^3}}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\\ = 2.\frac{{ - 75y + 2{y^3}}}{{\left( {25 - {y^2}} \right)\sqrt {25 - {y^2}} }}\end{array}\)
Thay \(y = \frac{{5\sqrt 2 }}{2}\) vào đạo hàm cấp 2 ta được:
\(S''\left( {\frac{{5\sqrt 2 }}{2}} \right) = 2.\frac{{ - 75.\left( {\frac{{5\sqrt 2 }}{2}} \right) + 2{{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^3}}}{{\left( {25 - {{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^2}} \right)\sqrt {25 - {{\left( {\frac{{5\sqrt 2 }}{2}} \right)}^2}} }} = - 8 < 0\)
Vì giá trị âm nên \(y = \frac{{5\sqrt 2 }}{2}\)là cực đại của hàm S.
Vậy A, B cách mặt đất một khoảng \(y = \frac{{5\sqrt 2 }}{2}\) thì diện tích hình chữ nhật ABCD là lớn nhất.
Giải Bài Tập 1.39 Trang 47 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu
Bài tập 1.39 trang 47 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm. Để giải bài tập này, các em cần nắm vững kiến thức về cách tính đạo hàm của hàm số, điều kiện cần và đủ để hàm số đạt cực trị, và cách khảo sát hàm số bằng đạo hàm.
Đề Bài Bài Tập 1.39 Trang 47 SGK Toán 12 Tập 1
(Đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Phương Pháp Giải Bài Tập 1.39 Trang 47 SGK Toán 12 Tập 1
- Bước 1: Tính đạo hàm cấp một (y') của hàm số.
- Bước 2: Tìm các điểm làm đạo hàm cấp một bằng 0 (y' = 0). Đây là các điểm nghi ngờ là điểm cực trị.
- Bước 3: Lập bảng biến thiên của hàm số. Xét dấu đạo hàm cấp một trên các khoảng xác định bởi các điểm tìm được ở bước 2.
- Bước 4: Kết luận về các điểm cực trị. Dựa vào bảng biến thiên, xác định các điểm cực đại, cực tiểu của hàm số.
Lời Giải Chi Tiết Bài Tập 1.39 Trang 47 SGK Toán 12 Tập 1
(Lời giải chi tiết sẽ được chèn vào đây, bao gồm các bước tính toán cụ thể và giải thích rõ ràng.)
Ví Dụ Minh Họa
Để giúp các em hiểu rõ hơn về phương pháp giải bài tập này, chúng ta sẽ xét một ví dụ cụ thể:
(Ví dụ minh họa sẽ được chèn vào đây, bao gồm đề bài, lời giải và giải thích.)
Lưu Ý Quan Trọng
- Luôn kiểm tra điều kiện xác định của hàm số trước khi tính đạo hàm.
- Chú ý đến dấu của đạo hàm cấp một để xác định khoảng đồng biến, nghịch biến của hàm số.
- Sử dụng đạo hàm cấp hai để xác định điểm uốn của hàm số (nếu cần).
Bài Tập Tương Tự
Để rèn luyện kỹ năng giải bài tập về đạo hàm, các em có thể tham khảo các bài tập tương tự sau:
- Bài tập 1.40 trang 47 SGK Toán 12 tập 1
- Bài tập 1.41 trang 48 SGK Toán 12 tập 1
Tusach.vn – Đồng Hành Cùng Các Em
Tusach.vn hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em sẽ tự tin hơn trong việc học tập môn Toán 12. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chương | Bài | Nội Dung |
|---|---|---|
| 1 | 1.39 | Giải bài tập trang 47 |