Lý thuyết Khảo sát và vẽ đồ thị của hàm số Toán 12 Cùng khám phá
Tổng quan nội dung
Lý thuyết Khảo sát và vẽ đồ thị hàm số Toán 12
Chương trình Toán 12 tập trung vào việc khảo sát và vẽ đồ thị hàm số, một phần quan trọng để nắm vững kiến thức nền tảng và chuẩn bị cho kỳ thi THPT Quốc gia. Tusach.vn cung cấp tài liệu đầy đủ, dễ hiểu về các phương pháp khảo sát hàm số và vẽ đồ thị một cách chính xác.
Bài viết này sẽ giúp bạn hệ thống lại kiến thức về các bước khảo sát hàm số, các yếu tố quan trọng cần xác định và cách vẽ đồ thị một cách chi tiết.
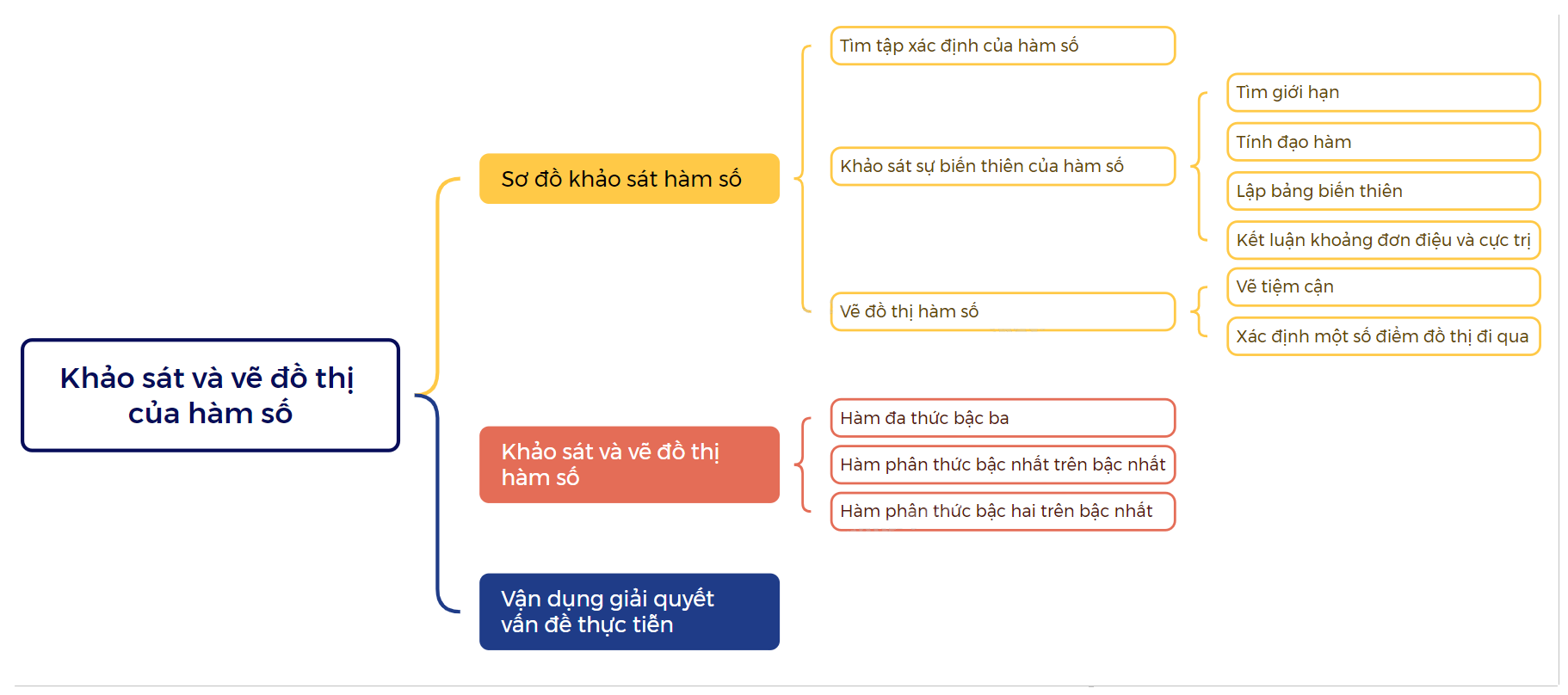
1. Sơ đồ khảo sát hàm số
1. Sơ đồ khảo sát hàm số
1. Tìm tập xác định của hàm số. 2. Khảo sát sự biến thiên của hàm số. - Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận (nếu có). - Lập BBT của hàm số bao gồm: tìm đạo hàm của hàm số, xét dấu đạo hàm, mô tả chiều biến thiên và cực trị của hàm số (nếu có), điền đầy đủ các kết quả vào bảng. - Dựa vào bảng, ta có kết luận về chiều biến thiên và cực trị. 3. Vẽ đồ thị hàm số. - Vẽ các đường tiệm cận của đồ thị (nếu có). - Xác định thêm một số điểm đặc biệt của đồ thị, chẳng hạn tìm giao điểm của đồ thị với các trục tọa độ (nếu đồ thị không cắt các trục tọa độ hoặc việc tìm các tọa độ giao điểm phức tạp thì bỏ qua phần này). - Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị. |
2. Khảo sát và vẽ đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d (a \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3} + 3{x^2} - 4\).
Tập xác định của hàm số: R.
Sự biến thiên:
Ta có: \(y' = - 3{x^2} + 6x\). Vậy y’ = 0 khi x = 0 hoặc x = 2
Trên khoảng \(\left( {0;2} \right)\), y’ > 0 nên hàm số đồng biến. Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó.
Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu \({y_{CT}} = - 4\). Hàm số đạt cực đại tại x = 2, giá trị cực đại.
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty \).
BBT:
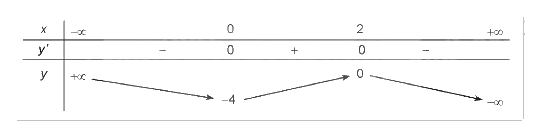
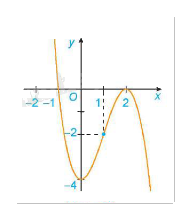
Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;4} \right)\).
Ta có: y = 0 \( \Leftrightarrow \)x = -1 hoặc x = 2. Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( { - 1;0} \right)\) và \(\left( {2;0} \right)\).
Đồ thị hàm số có tâm đối xứng là điểm \(\left( {1; - 2} \right)\).
3. Khảo sát và vẽ đồ thị hàm số\(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{x + 1}}{{x - 2}}\).
Tập xác định của hàm số: R\{2}.
Sự biến thiên:
Ta có: \(y' = - \frac{3}{{{{(x - 2)}^2}}} < 0\) với mọi \(x \ne 2\).
Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số không có cực trị.
Tiệm cận: \(\mathop {\lim }\limits_{x \to - \infty } y = 1;\mathop {\lim }\limits_{x \to + \infty } - \infty = 1\).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \).
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1.
BBT:
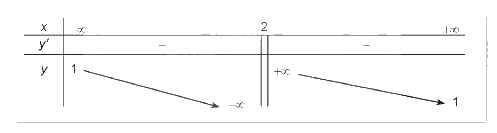
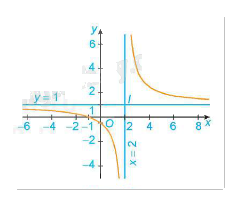
Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0; - \frac{1}{2}} \right)\).
Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 1;0} \right)\).
Đồ thị hàm số nhận giao điểm I \(\left( {2;1} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
4. Khảo sát và vẽ đồ thịhàm số\(y = \frac{{a{x^2} + bx + c}}{{px + q}}(a \ne 0,p \ne 0)\)(đa thức tử không chia hết cho đa thức mẫu)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2} - x - 1}}{{x - 2}}\).
Tập xác định của hàm số: R\{2}.
Sự biến thiên: Viết \(y = x + 1 + \frac{1}{{x - 2}}\).
Ta có: \(y' = 1 - \frac{1}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{(x - 2)}^2}}}\) . Vậy y’ = 0 \( \Leftrightarrow \) x = 1 hoặc x = 3.
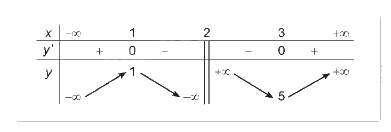
Trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\), y’ > 0 nên hàm số đồng biến trên từng khoảng này.
Trên các khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\), y’ < 0 nên hàm số nghịch biến trên từng khoảng này.
Hàm số đạt cực đại tại x = 1 với ; hàm số đạt cực tiểu tại x = 3 với \({y_{CT}} = 5\).
\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty \).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \).
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\); \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\).
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x + 1.
BBT:
Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;\frac{1}{2}} \right)\).
Ta có: \(y = 0 \Leftrightarrow x = \frac{{1 - \sqrt 5 }}{2};x = \frac{{1 + \sqrt 5 }}{2}\). Do đó giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( {\frac{{1 - \sqrt 5 }}{2};0} \right);\left( {\frac{{1 + \sqrt 5 }}{2};0} \right)\).
Đồ thị hàm số nhận giao điểm I \(\left( {2;3} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
5. Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan thực tiễn
Ví dụ: Khi một vật lạ mắc kẹt trong khí quản khiến ta phải ho, cơ hoành đẩy lên trên gây ra tăng áp lực trong phổi, theo đó cuống họng co thắt làm hẹp khí quản khiến không khí đi qua mạnh hơn. Đối với một lượng không khí bị đẩy ra trong một khoảng thời gian cố định, khí quản càng nhỏ thì luồng không khí càng đẩy ra nhanh hơn. Vận tốc luồng khí thoát ra càng cao, lực tác động lên vật càng lớn. Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc v của luồng khí liên hệ với bán kính x của khí quản theo công thức:
\(v(x) = k({x_0} - x){x^2}\) với \(\frac{1}{2}{x_0} \le x \le {x_0}\)
trong đó k là hằng số (k > 0) và \({x_0}\) là bán kính khí quản ở trạng thái bình thường. Tìm x theo \({x_0}\) để vận tốc của luồng khí một cơn ho trong trường hợp này là lớn nhất.
Giải:
Xét hàm số \(f(x) = ({x_0} - x){x^2}\) với \({x_0}\) cố định và \(\frac{1}{2}{x_0} \le x \le {x_0}\).
Do k là hằng số nên vận tốc của luồng khí một cơn ho lớn nhất khi f(x) đạt giá trị lớn nhất.
Ta có:
\(\begin{array}{l}f(x) = - {x^3} + {x_0}{x^2};\\f'(x) = - 3{x^2} + 2{x_0}x;\\f'(x) = 0 \Leftrightarrow x = 0,x = \frac{2}{3}{x_0}\end{array}\)
BBT:
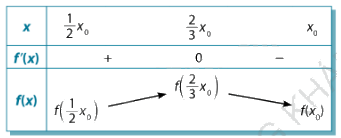
Dựa vào BBT, ta có \(\mathop {\max }\limits_{\left[ {\frac{1}{2}{x_0};{x_0}} \right]} f(x) = f\left( {\frac{2}{3}{x_0}} \right)\).
Vậy vận tốc của luồng khí một cơn ho lớn nhất khi \(x = \frac{2}{3}{x_0}\).
Lý Thuyết Khảo Sát và Vẽ Đồ Thị Hàm Số Toán 12: Hướng Dẫn Chi Tiết
Khảo sát và vẽ đồ thị hàm số là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 12, đóng vai trò then chốt trong việc củng cố kiến thức và chuẩn bị cho kỳ thi THPT Quốc gia. Tusach.vn xin giới thiệu hướng dẫn chi tiết về lý thuyết và phương pháp thực hiện, giúp bạn nắm vững kiến thức một cách hiệu quả nhất.
I. Các Bước Khảo Sát Hàm Số
- Xác định tập xác định: Tìm khoảng mà hàm số có nghĩa.
- Xét tính liên tục: Kiểm tra hàm số liên tục trên tập xác định hay không.
- Xét tính đơn điệu:
- Tính đạo hàm f'(x).
- Giải phương trình f'(x) = 0 để tìm điểm cực trị.
- Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến.
- Tìm cực trị: Xác định các điểm cực đại, cực tiểu của hàm số.
- Tìm điểm uốn: Tính đạo hàm bậc hai f''(x) và giải phương trình f''(x) = 0.
- Tìm tiệm cận:
- Tiệm cận đứng: x = a nếu lim f(x) = ±∞ khi x → a.
- Tiệm cận ngang: y = b nếu lim f(x) = b khi x → ±∞.
- Tiệm cận xiên: y = ax + b nếu lim (f(x) - (ax + b))/x = 0 khi x → ±∞.
- Lập bảng biến thiên: Tổng hợp các thông tin đã tìm được để vẽ đồ thị hàm số.
- Vẽ đồ thị: Dựa vào bảng biến thiên để vẽ đồ thị hàm số một cách chính xác.
II. Khảo Sát Hàm Số Bậc Ba
Hàm số bậc ba có dạng y = ax3 + bx2 + cx + d (a ≠ 0). Việc khảo sát hàm số bậc ba đòi hỏi sự hiểu biết về đạo hàm và các điểm cực trị. Điểm uốn của hàm số bậc ba luôn nằm giữa hai điểm cực trị.
III. Khảo Sát Hàm Số Bậc Bốn
Hàm số bậc bốn có dạng y = ax4 + bx3 + cx2 + dx + e (a ≠ 0). Khảo sát hàm số bậc bốn phức tạp hơn hàm số bậc ba, cần chú ý đến các trường hợp khác nhau của hệ số a và dấu của đạo hàm bậc hai.
IV. Ví Dụ Minh Họa
Ví dụ 1: Khảo sát hàm số y = x3 - 3x2 + 2.
- Tập xác định: R
- Đạo hàm: y' = 3x2 - 6x
- Giải y' = 0: x = 0 hoặc x = 2
- Bảng biến thiên: (Tự lập)
- Kết luận: Hàm số có cực đại tại x = 0, cực tiểu tại x = 2.
V. Luyện Tập và Bài Tập
Để nắm vững kiến thức, bạn nên luyện tập thêm các bài tập về khảo sát và vẽ đồ thị hàm số. Tusach.vn cung cấp nhiều bài tập đa dạng với các mức độ khó khác nhau để bạn rèn luyện kỹ năng.
VI. Mẹo Học Tập Hiệu Quả
- Nắm vững lý thuyết về đạo hàm và các điểm cực trị.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ vẽ đồ thị trực tuyến để kiểm tra kết quả.
- Tham khảo các tài liệu và video hướng dẫn trên Tusach.vn.
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc khảo sát và vẽ đồ thị hàm số Toán 12. Chúc bạn học tập tốt!