Giải mục 3 trang 28 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 28 SGK Toán 12 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 28 SGK Toán 12 tập 1. Bài viết này sẽ giúp các em hiểu rõ hơn về nội dung bài học và cách giải các bài tập liên quan.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp kiến thức chính xác và dễ hiểu nhất.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số (y = f(x) = frac{{2x + 4}}{{2x + 1}}).
VD2
Trả lời câu hỏi Vận dụng 2 trang 28 SGK Toán 12 Cùng khám phá
Ở một bể chứa nước có chứa 1000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào bể nước với tốc độ là 25 lít/phút.
a) Chứng minh rằng nồng độ muối của nước trong bể sau t phút kể từ khi bắt đầu bơm là: \(C(t) = \frac{{30t}}{{40 + t}}.\)
b) Khảo sát sự biến thiên của hàm số \(y = C(t)\) sau 10 tiếng kể từ lúc bắt đầu bơm, từ đó nhận xét về nồng độ muối trong bể khi thời gian ttt càng lớn.
Phương pháp giải:
a)
Tính lượng nước biển bơm vào sau 𝑡 phút.
Tính tổng lượng nước trong bể sau 𝑡 phút.
Tính lượng muối bơm vào bể sau 𝑡 phút.
Tính nồng độ muối 𝐶(𝑡).
b)
Tính giới hạn của C(t) khi \(t \to \infty \).
Tính đạo hàm của C(t).
Xét dấu của đạo hàm C’(t).
Từ dấu của đạo hàm và giới hạn khi \(t \to \infty \)kết luận về sự biến thiên và giá trị tiệm cận của hàm số.
Lời giải chi tiết:
a)
Lượng nước biển bơm vào sau \(t\) phút: \(V = 25t\) lít.
Tổng lượng nước trong bể sau \(t\) phút: \(1000 + 25t\) lít.
Lượng muối bơm vào bể sau \(t\) phút: \(30.25t = 750t {\rm{gam}}.\)
Nồng độ muối \(C(t) = \frac{{750t}}{{1000 + 25t}} = \frac{{750t}}{{25(40 + t)}} = \frac{{30t}}{{40 + t}}.\)
b)
Vì t là thời gian nên tập xác định của hàm số
\({\rm{y}} = C(t)\) là t > 0.
Giới hạn của \(C(t)\) khi \(t \to \infty \) : \(\mathop {\lim }\limits_{t \to \infty } \frac{{30t}}{{40 + t}} = 30.\)
Đạo hàm của \(C(t)\) : \({C^\prime }(t) = \frac{{30.(40 + t) - 30t.1}}{{{{(40 + t)}^2}}} = \frac{{1200 + 30t - 30t}}{{{{(40 + t)}^2}}} = \frac{{1200}}{{{{(40 + t)}^2}}}.\)
Nhận thấy \({C^\prime }(t) > 0\forall t > 0.\)
Vậy nồng độ muối trong bể tăng dần khi thời gian \(t\) càng lớn.
Khi \(t \to \infty \), nồng độ muối trong bể tiệm cận 30 gam/lít.
LT2
Trả lời câu hỏi Luyện tập 2 trang 28 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = f(x) = \frac{{2x + 4}}{{2x + 1}}.\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
- Tập xác định: \({\rm{D}} = {\rm{R}}\backslash \left\{ {\frac{{ - 1}}{2}} \right\}\).
- Sự biến thiên:
Giới hạn, tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
Suy ra đường thẳng \({\rm{y}} = 1\) là đường tiệm cận ngang của đồ thị hàm số đã cho
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} \frac{{2x + 4}}{{2x + 1}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} \frac{{2x + 4}}{{2x + 1}} = - \infty \)
Suy ra đường thẳng \({\rm{x}} = \frac{{ - 1}}{2}\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Ta có: \({y^\prime } = \frac{{ - 6}}{{{{(2x + 1)}^2}}} < 0.\)
Suy ra hàm số nghịch biến trên tập xác định.
Bảng biến thiên:
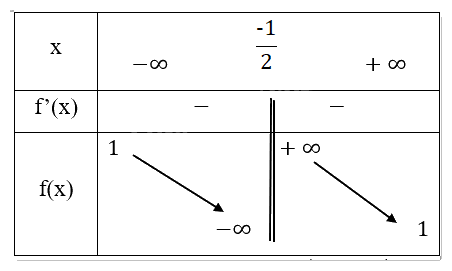
Chiều biến thiên: Hàm số nghịch biến trên \(\left( { - \infty ,\frac{{ - 1}}{2}} \right)\) và \(\left( {\frac{{ - 1}}{2}, + \infty } \right)\)
Cực trị: Hàm số không có cực trị.
- Vẽ đồ thị:
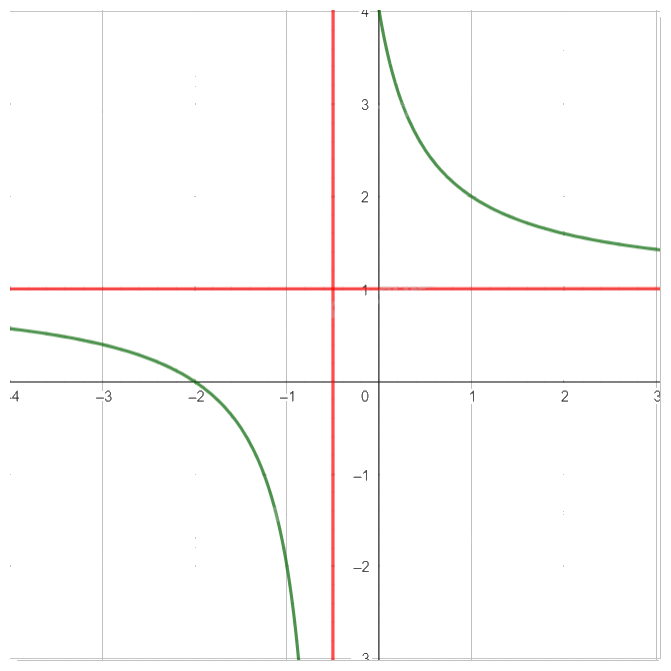
- LT2
- VD2
Trả lời câu hỏi Luyện tập 2 trang 28 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = f(x) = \frac{{2x + 4}}{{2x + 1}}.\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
- Tập xác định: \({\rm{D}} = {\rm{R}}\backslash \left\{ {\frac{{ - 1}}{2}} \right\}\).
- Sự biến thiên:
Giới hạn, tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
Suy ra đường thẳng \({\rm{y}} = 1\) là đường tiệm cận ngang của đồ thị hàm số đã cho
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} \frac{{2x + 4}}{{2x + 1}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} \frac{{2x + 4}}{{2x + 1}} = - \infty \)
Suy ra đường thẳng \({\rm{x}} = \frac{{ - 1}}{2}\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Ta có: \({y^\prime } = \frac{{ - 6}}{{{{(2x + 1)}^2}}} < 0.\)
Suy ra hàm số nghịch biến trên tập xác định.
Bảng biến thiên:
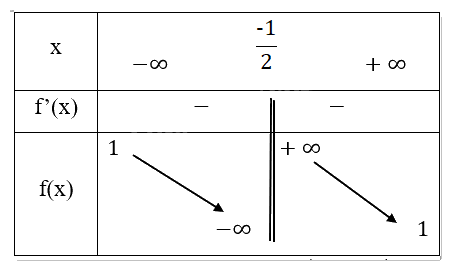
Chiều biến thiên: Hàm số nghịch biến trên \(\left( { - \infty ,\frac{{ - 1}}{2}} \right)\) và \(\left( {\frac{{ - 1}}{2}, + \infty } \right)\)
Cực trị: Hàm số không có cực trị.
- Vẽ đồ thị:
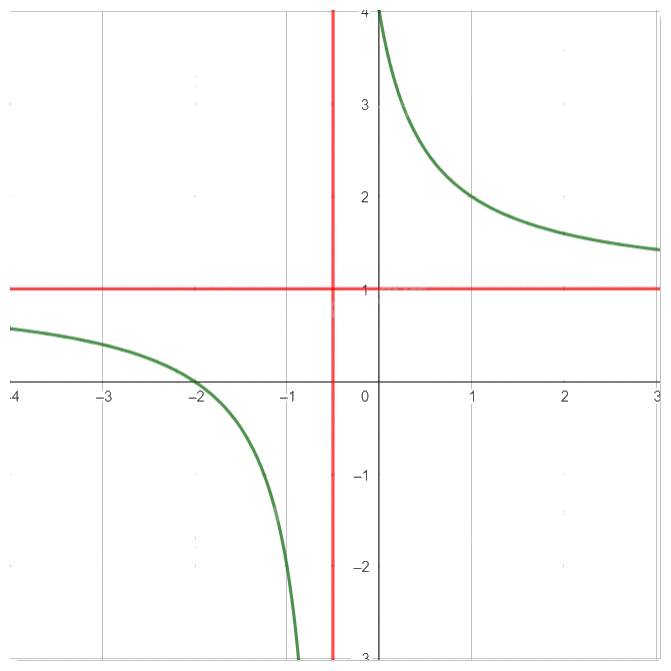
Trả lời câu hỏi Vận dụng 2 trang 28 SGK Toán 12 Cùng khám phá
Ở một bể chứa nước có chứa 1000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào bể nước với tốc độ là 25 lít/phút.
a) Chứng minh rằng nồng độ muối của nước trong bể sau t phút kể từ khi bắt đầu bơm là: \(C(t) = \frac{{30t}}{{40 + t}}.\)
b) Khảo sát sự biến thiên của hàm số \(y = C(t)\) sau 10 tiếng kể từ lúc bắt đầu bơm, từ đó nhận xét về nồng độ muối trong bể khi thời gian ttt càng lớn.
Phương pháp giải:
a)
Tính lượng nước biển bơm vào sau 𝑡 phút.
Tính tổng lượng nước trong bể sau 𝑡 phút.
Tính lượng muối bơm vào bể sau 𝑡 phút.
Tính nồng độ muối 𝐶(𝑡).
b)
Tính giới hạn của C(t) khi \(t \to \infty \).
Tính đạo hàm của C(t).
Xét dấu của đạo hàm C’(t).
Từ dấu của đạo hàm và giới hạn khi \(t \to \infty \)kết luận về sự biến thiên và giá trị tiệm cận của hàm số.
Lời giải chi tiết:
a)
Lượng nước biển bơm vào sau \(t\) phút: \(V = 25t\) lít.
Tổng lượng nước trong bể sau \(t\) phút: \(1000 + 25t\) lít.
Lượng muối bơm vào bể sau \(t\) phút: \(30.25t = 750t {\rm{gam}}.\)
Nồng độ muối \(C(t) = \frac{{750t}}{{1000 + 25t}} = \frac{{750t}}{{25(40 + t)}} = \frac{{30t}}{{40 + t}}.\)
b)
Vì t là thời gian nên tập xác định của hàm số
\({\rm{y}} = C(t)\) là t > 0.
Giới hạn của \(C(t)\) khi \(t \to \infty \) : \(\mathop {\lim }\limits_{t \to \infty } \frac{{30t}}{{40 + t}} = 30.\)
Đạo hàm của \(C(t)\) : \({C^\prime }(t) = \frac{{30.(40 + t) - 30t.1}}{{{{(40 + t)}^2}}} = \frac{{1200 + 30t - 30t}}{{{{(40 + t)}^2}}} = \frac{{1200}}{{{{(40 + t)}^2}}}.\)
Nhận thấy \({C^\prime }(t) > 0\forall t > 0.\)
Vậy nồng độ muối trong bể tăng dần khi thời gian \(t\) càng lớn.
Khi \(t \to \infty \), nồng độ muối trong bể tiệm cận 30 gam/lít.
Giải mục 3 trang 28 SGK Toán 12 tập 1 - Cùng khám phá: Tổng quan và Phương pháp
Mục 3 trang 28 SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học tiếp theo và các kỳ thi quan trọng.
Nội dung chi tiết Giải mục 3 trang 28 SGK Toán 12 tập 1
Để giúp các em hiểu rõ hơn, chúng ta sẽ đi sâu vào từng bài tập cụ thể trong mục 3 trang 28. Dưới đây là phân tích chi tiết và lời giải cho từng bài:
Bài 1: Tính đạo hàm của hàm số
Bài tập này yêu cầu các em áp dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của các hàm số cho trước. Ví dụ:
- Hàm số: y = x3 + 2x2 - 5x + 1
- Lời giải: y' = 3x2 + 4x - 5
Bài 2: Tìm đạo hàm cấp hai
Bài tập này yêu cầu các em tìm đạo hàm cấp hai của hàm số, tức là đạo hàm của đạo hàm cấp nhất. Ví dụ:
- Hàm số: y = sin(x)
- Lời giải: y' = cos(x), y'' = -sin(x)
Bài 3: Ứng dụng đạo hàm để tìm cực trị
Bài tập này yêu cầu các em sử dụng đạo hàm để tìm các điểm cực trị của hàm số. Các bước thực hiện:
- Tìm đạo hàm y'
- Giải phương trình y' = 0 để tìm các điểm dừng
- Xét dấu của đạo hàm y' để xác định các điểm cực đại, cực tiểu
Phương pháp giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, các em cần:
- Nắm vững các quy tắc tính đạo hàm: Quy tắc lũy thừa, quy tắc tích, quy tắc thương, quy tắc chuỗi,...
- Thành thạo đạo hàm của các hàm số cơ bản: sin(x), cos(x), tan(x), ex, ln(x),...
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
Bảng tổng hợp các công thức đạo hàm quan trọng
| Hàm số | Đạo hàm |
|---|---|
| y = xn | y' = nxn-1 |
| y = sin(x) | y' = cos(x) |
| y = cos(x) | y' = -sin(x) |
| y = ex | y' = ex |
Lưu ý khi giải bài tập đạo hàm
Khi giải bài tập đạo hàm, các em cần chú ý:
- Kiểm tra kỹ các điều kiện xác định của hàm số.
- Sử dụng đúng các quy tắc tính đạo hàm.
- Kiểm tra lại kết quả sau khi tính toán.
Hy vọng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải các bài tập trong mục 3 trang 28 SGK Toán 12 tập 1. Chúc các em học tập tốt!