Giải bài tập 2.11 trang 65 SGK Toán 12 tập 1
Bài tập 2.11 trang 65 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.
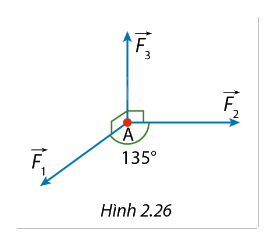
Một chất điểm (A) nằm trên mặt phẳng nằm ngang ((alpha )), chịu tác động bởi ba lực ({vec F_1},{vec F_{{2^prime }}}{vec F_3}). Các lực ({vec F_1},{vec F_2}) có giá nằm trong ((alpha )) và (left( {{{vec F}_1},{{vec F}_2}} right) = {135^circ }), còn lực ({vec F_3}) có giá vuông góc với ( (alpha ) ) và hướng lên trên. Xác định hợp lực của các lực ({vec F_1},{vec F_2},{vec F_3}), biết rằng độ lớn của ba lực đó lần lượt là 20N, 15N và 10N.
Giải bài tập 2.11 trang 65 SGK Toán 12 tập 1: Phương pháp và đáp án chi tiết
Bài tập 2.11 trang 65 SGK Toán 12 tập 1 thuộc chương trình Giải tích, cụ thể là phần Đạo hàm. Bài toán này thường yêu cầu học sinh áp dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của thương. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Đề bài bài tập 2.11 trang 65 SGK Toán 12 tập 1
(Đề bài cụ thể của bài tập 2.11 sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) = (x^2 + 1)/(x - 2). Tính f'(x).)
Phương pháp giải bài tập 2.11 trang 65 SGK Toán 12 tập 1
Để giải bài tập này, chúng ta cần áp dụng quy tắc đạo hàm của thương:
Nếu y = u(x) / v(x) thì y' = (u'(x)v(x) - u(x)v'(x)) / (v(x))^2
Trong đó:
- u(x) là hàm số ở tử
- v(x) là hàm số ở mẫu
- u'(x) là đạo hàm của u(x)
- v'(x) là đạo hàm của v(x)
Lời giải chi tiết bài tập 2.11 trang 65 SGK Toán 12 tập 1
(Lời giải chi tiết của bài tập 2.11 sẽ được trình bày ở đây, bao gồm các bước tính toán cụ thể và giải thích rõ ràng. Ví dụ:
- Đặt u(x) = x^2 + 1 và v(x) = x - 2
- Tính đạo hàm u'(x) = 2x và v'(x) = 1
- Áp dụng quy tắc đạo hàm của thương: f'(x) = (2x(x - 2) - (x^2 + 1)(1)) / (x - 2)^2
- Rút gọn biểu thức: f'(x) = (2x^2 - 4x - x^2 - 1) / (x - 2)^2 = (x^2 - 4x - 1) / (x - 2)^2
Vậy, f'(x) = (x^2 - 4x - 1) / (x - 2)^2)
Lưu ý khi giải bài tập 2.11 trang 65 SGK Toán 12 tập 1
- Luôn kiểm tra kỹ đề bài để xác định đúng hàm số u(x) và v(x).
- Tính đạo hàm u'(x) và v'(x) một cách chính xác.
- Áp dụng đúng quy tắc đạo hàm của thương.
- Rút gọn biểu thức đạo hàm một cách cẩn thận.
Bài tập tương tự và luyện tập thêm
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 và các tài liệu luyện thi Toán THPT Quốc gia. tusach.vn sẽ tiếp tục cập nhật thêm nhiều bài giải và phương pháp giải toán hữu ích khác.
Kết luận
Bài tập 2.11 trang 65 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm của hàm số. Hy vọng với lời giải chi tiết và phương pháp giải khoa học mà tusach.vn cung cấp, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
