Giải mục 4 trang 30 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 4 trang 30 SGK Toán 12 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 30 SGK Toán 12 tập 1. Bài viết này sẽ giúp các em hiểu rõ hơn về kiến thức trọng tâm và cách giải các bài tập liên quan.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây: a) (y = frac{{ - {x^2} - 2x - 2}}{{x + 1}}) b) ({rm{y}} = frac{{{x^2} - 2x - 3}}{{x - 2}})
LT3
Trả lời câu hỏi Luyện tập 3 trang 30 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây:
a) \(y = \frac{{ - {x^2} - 2x - 2}}{{x + 1}}\)
b) \({\rm{y}} = \frac{{{x^2} - 2x - 3}}{{x - 2}}\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
a)
- Tập xác định: D = R \ {-1}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = - \infty .\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = \infty .\)
Suy ra x = -1 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } [ - (x + 1)] - 0 = - \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - \infty } [ - (x + 1)] - 0 = \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{ - {x^2} - 2x - 2}}{{x + 1}} = - x - 1 + \frac{{ - 1}}{{x + 1}}\) (Sử dụng phép chia đa thức)
Khi \(x \to \pm \infty ,\frac{{ - 1}}{{x + 1}} \to 0\) nên \(y = - x - 1\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{ - (2x + 2)(x + 1) + \left( {{x^2} + 2x + 2} \right)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\).
\({y^\prime } = 0 \leftrightarrow - {x^2} - 2x \leftrightarrow - x(x + 2) = 0 \leftrightarrow x = 0,{\rm{ }}x = - 2\).
Bảng biến thiên:
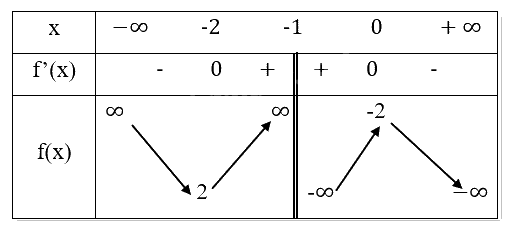
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,-2) và (-1,0), đồng biến trên khoảng (-2,-1) và (-1,0).
Cực trị: Hàm số đạt cực tiểu tại \(x = - 2,{y_{CT}} = 2\).
Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = - 2\).
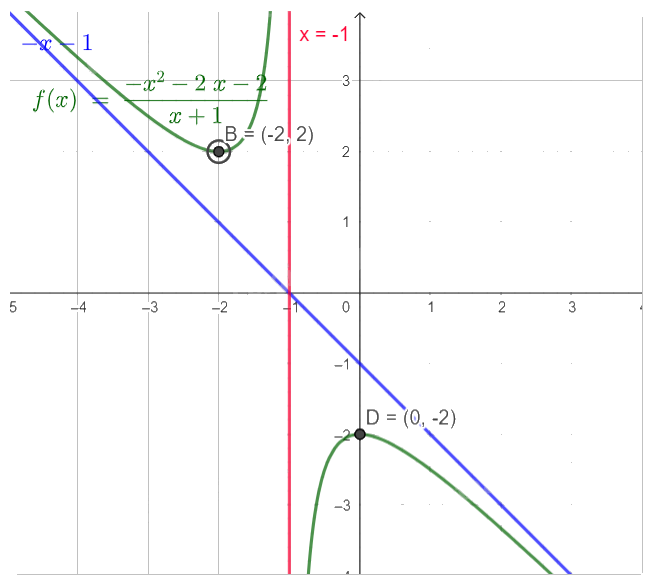
- Vẽ đồ thị:
Tiệm cận đứng \({\rm{x}} = - 1\), tiệm cận xiên \(y = - x - 1\).
Giao điểm với trục Oy là \((0, - 2)\).
b)
- Tập xác định: D = R \ {2}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to 2 + } y = \mathop {\lim }\limits_{x \to 2 + } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
Suy ra x = 2 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{{x^2} - 2x - 3}}{{x - 2}} = x + \frac{{ - 3}}{{x + 1}}\) .
Khi \(x \to \pm \infty ,\frac{{ - 3}}{{x + 1}} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{(2x - 2)(x - 2) - \left( {{x^2} - 2x - 3} \right)}}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\forall x \in D\).
Vậy hàm số đồng biến trên tập xác định.
Bảng biến thiên:
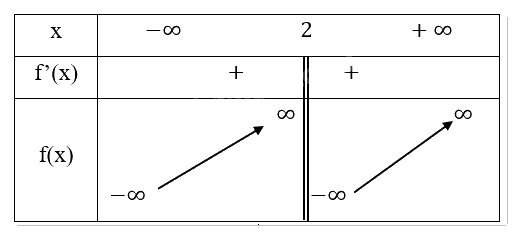
Chiều biến thiên: Hàm số đồng biến trên khoảng (-\(\infty ,2\)) và (2,\(\infty \)).
Cực trị: Hàm số không có cực trị.
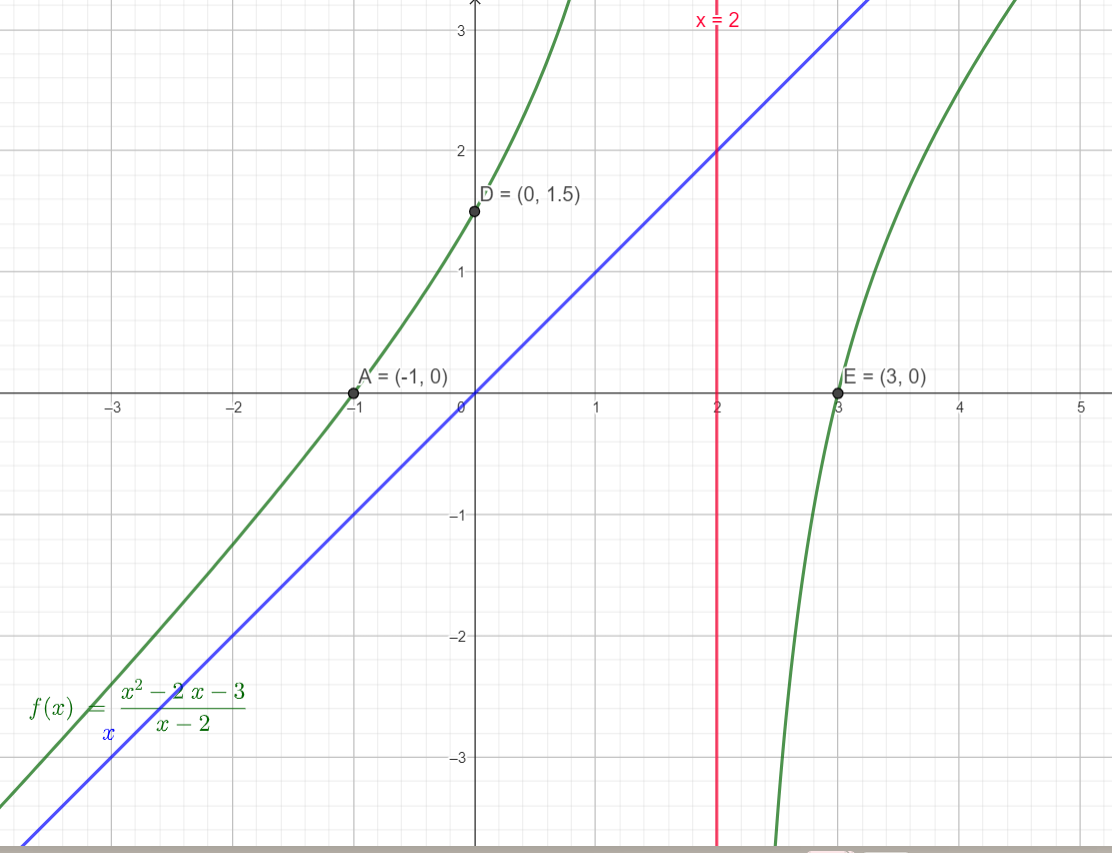
- Vẽ đồ thị:
Tiệm cận đứng x = 2, tiệm cận xiên y = x.
Giao điểm với trục Oy là (0,\(\frac{3}{2}\)).
Giao điểm với trục Ox là (-1,0) và (3,0).
- LT3
Trả lời câu hỏi Luyện tập 3 trang 30 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây:
a) \(y = \frac{{ - {x^2} - 2x - 2}}{{x + 1}}\)
b) \({\rm{y}} = \frac{{{x^2} - 2x - 3}}{{x - 2}}\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
a)
- Tập xác định: D = R \ {-1}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = - \infty .\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = \infty .\)
Suy ra x = -1 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } [ - (x + 1)] - 0 = - \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - \infty } [ - (x + 1)] - 0 = \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{ - {x^2} - 2x - 2}}{{x + 1}} = - x - 1 + \frac{{ - 1}}{{x + 1}}\) (Sử dụng phép chia đa thức)
Khi \(x \to \pm \infty ,\frac{{ - 1}}{{x + 1}} \to 0\) nên \(y = - x - 1\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{ - (2x + 2)(x + 1) + \left( {{x^2} + 2x + 2} \right)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\).
\({y^\prime } = 0 \leftrightarrow - {x^2} - 2x \leftrightarrow - x(x + 2) = 0 \leftrightarrow x = 0,{\rm{ }}x = - 2\).
Bảng biến thiên:
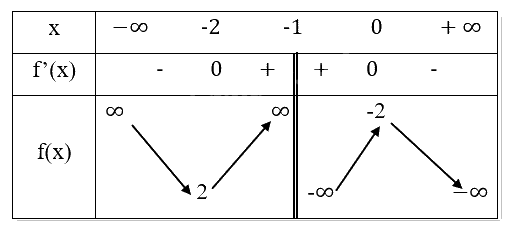
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,-2) và (-1,0), đồng biến trên khoảng (-2,-1) và (-1,0).
Cực trị: Hàm số đạt cực tiểu tại \(x = - 2,{y_{CT}} = 2\).
Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = - 2\).
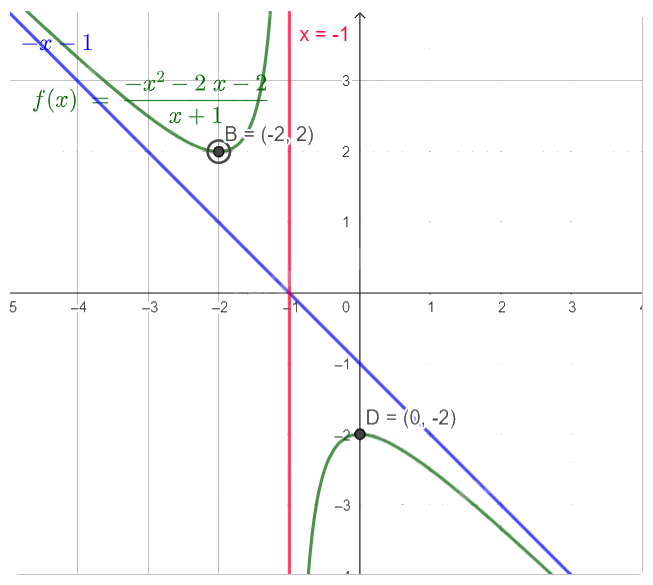
- Vẽ đồ thị:
Tiệm cận đứng \({\rm{x}} = - 1\), tiệm cận xiên \(y = - x - 1\).
Giao điểm với trục Oy là \((0, - 2)\).
b)
- Tập xác định: D = R \ {2}.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to 2 + } y = \mathop {\lim }\limits_{x \to 2 + } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
\(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
Suy ra x = 2 là tiệm cận đứng của hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \).
Suy ra hàm số không có tiệm cận ngang
\(\frac{{{x^2} - 2x - 3}}{{x - 2}} = x + \frac{{ - 3}}{{x + 1}}\) .
Khi \(x \to \pm \infty ,\frac{{ - 3}}{{x + 1}} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = \frac{{(2x - 2)(x - 2) - \left( {{x^2} - 2x - 3} \right)}}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\forall x \in D\).
Vậy hàm số đồng biến trên tập xác định.
Bảng biến thiên:
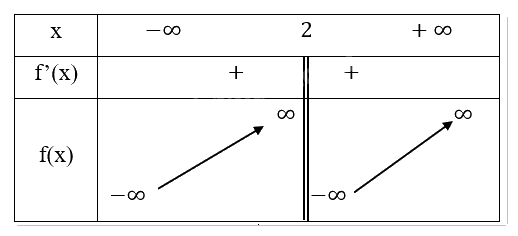
Chiều biến thiên: Hàm số đồng biến trên khoảng (-\(\infty ,2\)) và (2,\(\infty \)).
Cực trị: Hàm số không có cực trị.
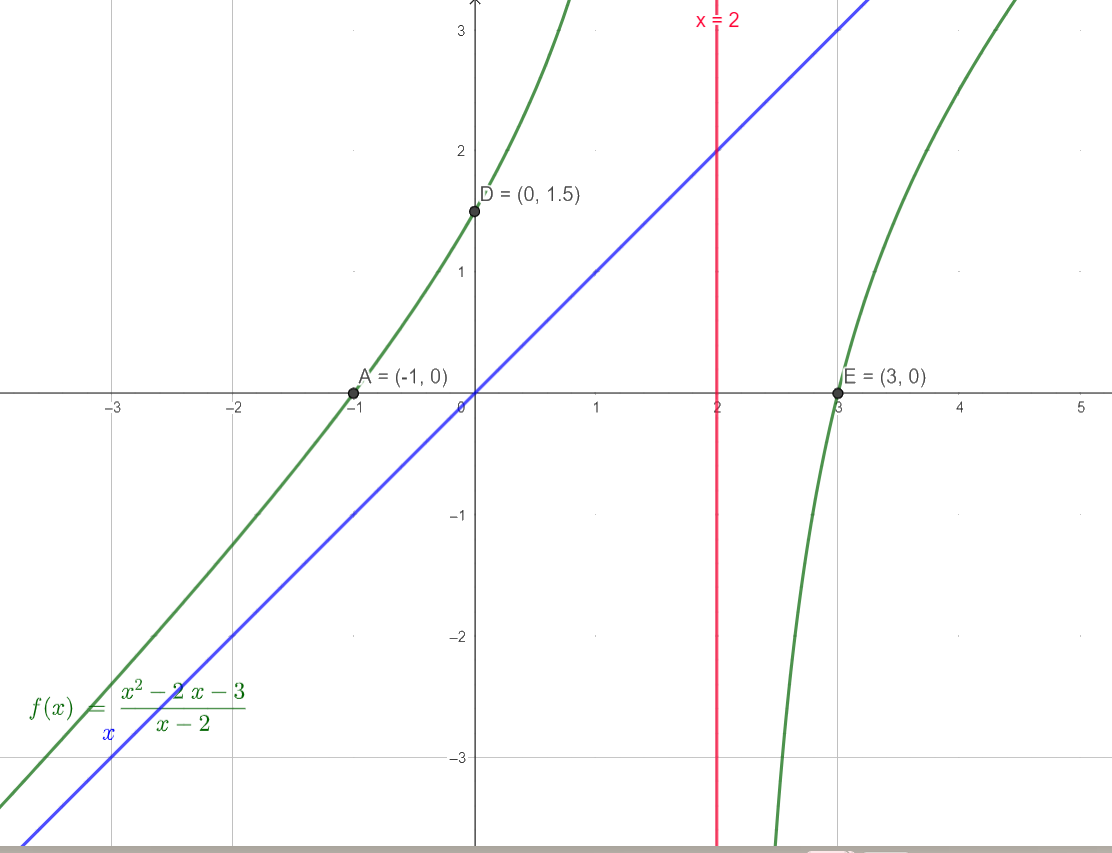
- Vẽ đồ thị:
Tiệm cận đứng x = 2, tiệm cận xiên y = x.
Giao điểm với trục Oy là (0,\(\frac{3}{2}\)).
Giao điểm với trục Ox là (-1,0) và (3,0).
Giải mục 4 trang 30 SGK Toán 12 tập 1 - Cùng khám phá: Tổng quan và Phương pháp giải
Mục 4 trang 30 SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các dạng bài tập tính đạo hàm, ứng dụng đạo hàm để khảo sát hàm số và giải các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp cao hơn.
I. Kiến thức trọng tâm cần nắm vững
- Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và đạo hàm của hàm số trên một khoảng.
- Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, đạo hàm của hàm hợp.
- Đạo hàm của các hàm số cơ bản: Biết đạo hàm của các hàm số thường gặp như hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit.
- Ứng dụng đạo hàm: Hiểu cách sử dụng đạo hàm để khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn) và giải các bài toán tối ưu.
II. Các dạng bài tập thường gặp và phương pháp giải
- Tính đạo hàm:
Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh áp dụng các quy tắc tính đạo hàm để tìm đạo hàm của hàm số cho trước. Cần chú ý đến việc biến đổi biểu thức đại số trước khi tính đạo hàm để đơn giản hóa bài toán.
- Khảo sát hàm số:
Dạng bài tập này yêu cầu học sinh sử dụng đạo hàm để xác định các yếu tố quan trọng của hàm số như khoảng đồng biến, nghịch biến, cực trị, điểm uốn. Việc vẽ đồ thị hàm số cũng là một phần quan trọng của việc khảo sát hàm số.
- Giải bài toán tối ưu:
Đây là dạng bài tập ứng dụng đạo hàm để giải các bài toán thực tế như tìm giá trị lớn nhất, giá trị nhỏ nhất của một đại lượng nào đó. Cần xác định đúng hàm số cần tối ưu và tìm các điểm cực trị của hàm số đó.
III. Ví dụ minh họa giải mục 4 trang 30 SGK Toán 12 tập 1
Bài tập: Tính đạo hàm của hàm số y = x3 - 2x2 + 5x - 1.
Giải:
y' = 3x2 - 4x + 5
IV. Luyện tập và củng cố kiến thức
Để nắm vững kiến thức và kỹ năng giải các bài tập về đạo hàm, các em nên luyện tập thường xuyên với các bài tập trong SGK, sách bài tập và các đề thi thử. Ngoài ra, các em có thể tham khảo các tài liệu học tập trực tuyến trên tusach.vn để có thêm nhiều bài tập và lời giải chi tiết.
V. Mẹo học tập hiệu quả
- Nắm vững định nghĩa và các quy tắc tính đạo hàm.
- Luyện tập thường xuyên với các bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị.
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
tusach.vn hy vọng rằng bài viết này sẽ giúp các em học sinh hiểu rõ hơn về Giải mục 4 trang 30 SGK Toán 12 tập 1 và tự tin hơn trong quá trình học tập. Chúc các em học tốt!