Giải mục 2 trang 5,6,7 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 5,6,7 SGK Toán 12 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 5,6,7 SGK Toán 12 tập 1. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, giúp các em hiểu rõ kiến thức và tự tin làm bài tập.
Mục 2 này tập trung vào các kiến thức cơ bản về... (điền kiến thức chính của mục 2 vào đây). Chúng tôi sẽ đi qua từng bài tập, giải thích rõ ràng từng bước để các em có thể nắm bắt được phương pháp giải.
Cực trị của hàm số
LT3
Trả lời câu hỏi Luyện tập 3 trang 6 SGK Toán 12 Kết nối tri thức
Chỉ ra một điểm cực đại, một điểm cực tiểu của đồ thị hàm số được cho ở hoạt động 3
Phương pháp giải:
Áp dụng định nghĩa về cực trị:
Cho hàm số \(y = f(x)\)liên tục trên khoảng \((a;b)\) và điểm \({x_0} \in (a;b)\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) < f({x_0})\)với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt cực đại tại \({x_0}\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) > f({x_0})\) với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt tiểu đại tại \({x_0}\)
Lời giải chi tiết:
Theo định nghĩa, ta có thể chọn\(h = 1\) ta có, \({x_0} - h = - 3\)và \({x_0} + h = - 1\)
Dựa vào đồ thị hàm số, ta có
\(f(x) > f( - 2)\), với\(\forall x \in ( - 3; - 1)\backslash \{ - 2\} \)
Suy ra \({x_0} = - 2\) là điểm cực tiểu của đồ thị hàm số
Theo định nghĩa, ta có thể chọn \(h = \frac{1}{2}\) ta có, \({x_0} - h = \frac{3}{2}\) và\({x_0} + h = \frac{5}{2}\)
Dựa vào đồ thị hàm số, ta có
\(f(x) < f(2)\) với \(\forall x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\backslash \{ 2\} \)
Suy ra \({x_0} = 2\) là điểm đại của đồ thị hàm số
LT5
Trả lời câu hỏi Luyện tập 5 trang 8 SGK Toán 12 Kết nối tri thức
Tìm cực trị của hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\)
Phương pháp giải:
Bước 1: Tính \(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định cực trị của hàm số
Lời giải chi tiết:
Hàm số trên xác định trên \(R/\{ 2\} \)
Ta có: \(f'(x) = \frac{{3(x - 2) - (3x + 1)}}{{{{(x - 2)}^2}}}\)
\(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}}\)
Vì \(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}} < 0\) với \(x \in R/\{ 2\} \)
Nên hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\) không có cực trị.
LT4
Trả lời câu hỏi Luyện tập 4 trang 7 SGK Toán 12 Kết nối tri thức
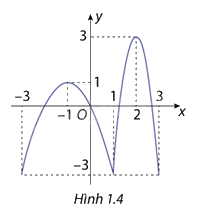
Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\left[ { - 3;3} \right]\)và có đồ thị hàm số như hình 1.4. Hãy xác định các điểm cực trị của hàm số trên khoảng\(\left( { - 3;3} \right)\)
Phương pháp giải:
Dựa vào đồ thị hàm số.
Lời giải chi tiết:
Dựa vào đồ thị hàm số, hàm số có 3 điểm cực trị là-1;1;2
Với điểm có cực trị là -1 thì giá trị cực trị là 1
Với điểm có cực trị là 1 thì giá trị cực trị là -3
Với điểm có cực trị là 2 thì giá trị cực trị là 3
VD
Trả lời câu hỏi Vận dụng trang 8 SGK Toán 12 Kết nối tri thức
Trở lại bài toán Khởi động ban đầu bài học, hãy lập bảng biến thiên của hàm số \(y = C(x) = \frac{{30x}}{{{x^2} + 2}}\)trên khoảng \((0; + \infty )\)
Khi đó, cho biết hàm nồng độ thước trong máu :
a) Tăng trong khoảng thời gian nào
b) Đạt giá trị cực đại là bao nhiêu trong khoảng thời gian 6 phút sau khi tiêm
Phương pháp giải:
Bước 1: Tính \(C'(x)\)
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính hàm nồng độ thước trong máu tăng trong khoảng thời gian nào là tính hàm số \(C(x)\) tăng trong khoảng nào hay hàm số \(C(x)\)đồng biến trong khoảng nào
Bước 4: Nồng độ thước máu đạt cực đại là bao nhiêu trong 6 phút sau khi tiêm là giá trị cực đại của hàm số \(C(x)\) trong khoảng \((0;6)\)
Lời giải chi tiết:
Hàm số trên xác định trên R
Ta có: \(y' = C'(x) = \frac{{30({x^2} + 2) - 30x.2x}}{{{{({x^2} + 2)}^2}}}\)
\( = \frac{{ - 30{x^2} + 60}}{{{{({x^2} + 2)}^2}}}\)
Xét \(y' = 0\) \( \Rightarrow - 30{x^2} + 60 = 0\) \( \Leftrightarrow x = \sqrt 2 \)
Ta có bảng biến thiên:
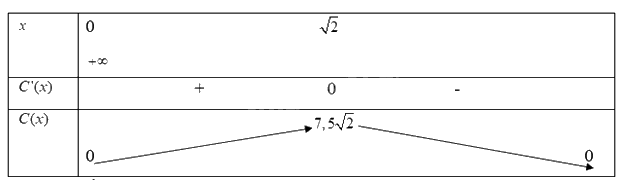
Từ bảng biến thiên, ta có :
a) Hàm số \(C(x)\)đồng biến trên khoảng \((0;7,5\sqrt 2 )\)hay nồng độ thước máu tăng từ sau khi tiêm đến \(7,5\sqrt 2 \)phút sau.
b) Hàm số \(C(x)\) đạt giá trị cực đại tại \(x = \sqrt 2 \)hay nồng độ thức máu đạt giá trị cực đại sau \(\sqrt 2 \) phút
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 5 SGK Toán 12 Kết nối tri thức
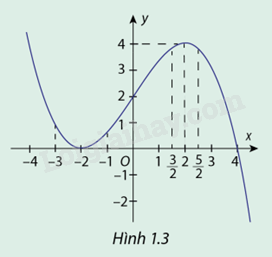
Hàm số \(y = f(x) = - \frac{1}{8}{x^3} + \frac{3}{2}x + 2\) có đồ thị cho ở hình 1.3
a) Giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị, só sánh \(f( - 2)\) với các giá trị khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, só sánh \(f(2)\) với các giá trị khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Phương pháp giải:
a) Tính \(f'(x)\) rồi giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị hàm số rồi giải
Lời giải chi tiết:
a) Ta có: \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2}\)
Xét \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2} = 0\)
\( \Rightarrow {x^2} = 4\)
\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
b) Dựa vào đồ thị, giá trị của \(f( - 2)\) luôn bé hơn các giá trị \(f(x)\) khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, giá trị của \(f(2)\)luôn lớn hơn các giá trị\(f(x)\) khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 6 SGK Toán 12 Kết nối tri thức
Xét hàm số ở hoạt động 3. Xác định dấu của đạo hàm ở các ô  tương ứng với thuộc các khoảng trong bảng 1.2. Nêu mỗi liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
tương ứng với thuộc các khoảng trong bảng 1.2. Nêu mỗi liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
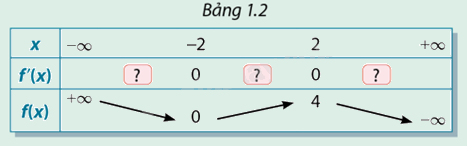
Phương pháp giải:
Dựa vào đồ thị hàm số, nếu đồ thị hàm số\(f(x)\) đi xuống thì \(f'(x)\)mang dấu (-)và ngược lại, nếu đồ thị hàm số\(f(x)\) đi lên thì \(f'(x)\) mang dấu (+).
Nhìn vào điểm cực trị trên bảng biến thiên rồi nhận xét.
Lời giải chi tiết:
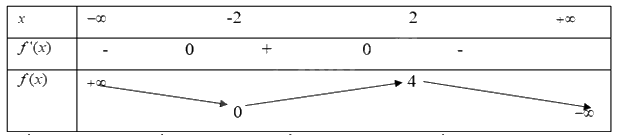
Mối liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm là: Nếu đạo hàm có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
- HĐ3
- LT3
- HĐ4
- LT4
- LT5
- VD
Trả lời câu hỏi Hoạt động 3 trang 5 SGK Toán 12 Kết nối tri thức
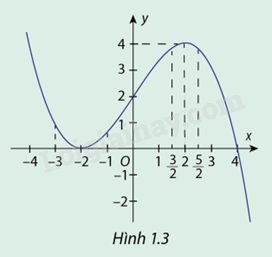
Hàm số \(y = f(x) = - \frac{1}{8}{x^3} + \frac{3}{2}x + 2\) có đồ thị cho ở hình 1.3
a) Giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị, só sánh \(f( - 2)\) với các giá trị khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, só sánh \(f(2)\) với các giá trị khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Phương pháp giải:
a) Tính \(f'(x)\) rồi giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị hàm số rồi giải
Lời giải chi tiết:
a) Ta có: \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2}\)
Xét \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2} = 0\)
\( \Rightarrow {x^2} = 4\)
\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
b) Dựa vào đồ thị, giá trị của \(f( - 2)\) luôn bé hơn các giá trị \(f(x)\) khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, giá trị của \(f(2)\)luôn lớn hơn các giá trị\(f(x)\) khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Trả lời câu hỏi Luyện tập 3 trang 6 SGK Toán 12 Kết nối tri thức
Chỉ ra một điểm cực đại, một điểm cực tiểu của đồ thị hàm số được cho ở hoạt động 3
Phương pháp giải:
Áp dụng định nghĩa về cực trị:
Cho hàm số \(y = f(x)\)liên tục trên khoảng \((a;b)\) và điểm \({x_0} \in (a;b)\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) < f({x_0})\)với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt cực đại tại \({x_0}\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) > f({x_0})\) với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt tiểu đại tại \({x_0}\)
Lời giải chi tiết:
Theo định nghĩa, ta có thể chọn\(h = 1\) ta có, \({x_0} - h = - 3\)và \({x_0} + h = - 1\)
Dựa vào đồ thị hàm số, ta có
\(f(x) > f( - 2)\), với\(\forall x \in ( - 3; - 1)\backslash \{ - 2\} \)
Suy ra \({x_0} = - 2\) là điểm cực tiểu của đồ thị hàm số
Theo định nghĩa, ta có thể chọn \(h = \frac{1}{2}\) ta có, \({x_0} - h = \frac{3}{2}\) và\({x_0} + h = \frac{5}{2}\)
Dựa vào đồ thị hàm số, ta có
\(f(x) < f(2)\) với \(\forall x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\backslash \{ 2\} \)
Suy ra \({x_0} = 2\) là điểm đại của đồ thị hàm số
Trả lời câu hỏi Hoạt động 4 trang 6 SGK Toán 12 Kết nối tri thức
Xét hàm số ở hoạt động 3. Xác định dấu của đạo hàm ở các ô  tương ứng với thuộc các khoảng trong bảng 1.2. Nêu mỗi liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
tương ứng với thuộc các khoảng trong bảng 1.2. Nêu mỗi liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
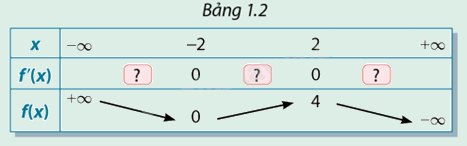
Phương pháp giải:
Dựa vào đồ thị hàm số, nếu đồ thị hàm số\(f(x)\) đi xuống thì \(f'(x)\)mang dấu (-)và ngược lại, nếu đồ thị hàm số\(f(x)\) đi lên thì \(f'(x)\) mang dấu (+).
Nhìn vào điểm cực trị trên bảng biến thiên rồi nhận xét.
Lời giải chi tiết:
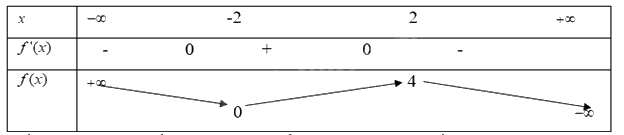
Mối liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm là: Nếu đạo hàm có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Trả lời câu hỏi Luyện tập 4 trang 7 SGK Toán 12 Kết nối tri thức
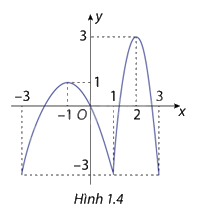
Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\left[ { - 3;3} \right]\)và có đồ thị hàm số như hình 1.4. Hãy xác định các điểm cực trị của hàm số trên khoảng\(\left( { - 3;3} \right)\)
Phương pháp giải:
Dựa vào đồ thị hàm số.
Lời giải chi tiết:
Dựa vào đồ thị hàm số, hàm số có 3 điểm cực trị là-1;1;2
Với điểm có cực trị là -1 thì giá trị cực trị là 1
Với điểm có cực trị là 1 thì giá trị cực trị là -3
Với điểm có cực trị là 2 thì giá trị cực trị là 3
Trả lời câu hỏi Luyện tập 5 trang 8 SGK Toán 12 Kết nối tri thức
Tìm cực trị của hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\)
Phương pháp giải:
Bước 1: Tính \(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định cực trị của hàm số
Lời giải chi tiết:
Hàm số trên xác định trên \(R/\{ 2\} \)
Ta có: \(f'(x) = \frac{{3(x - 2) - (3x + 1)}}{{{{(x - 2)}^2}}}\)
\(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}}\)
Vì \(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}} < 0\) với \(x \in R/\{ 2\} \)
Nên hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\) không có cực trị.
Trả lời câu hỏi Vận dụng trang 8 SGK Toán 12 Kết nối tri thức
Trở lại bài toán Khởi động ban đầu bài học, hãy lập bảng biến thiên của hàm số \(y = C(x) = \frac{{30x}}{{{x^2} + 2}}\)trên khoảng \((0; + \infty )\)
Khi đó, cho biết hàm nồng độ thước trong máu :
a) Tăng trong khoảng thời gian nào
b) Đạt giá trị cực đại là bao nhiêu trong khoảng thời gian 6 phút sau khi tiêm
Phương pháp giải:
Bước 1: Tính \(C'(x)\)
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính hàm nồng độ thước trong máu tăng trong khoảng thời gian nào là tính hàm số \(C(x)\) tăng trong khoảng nào hay hàm số \(C(x)\)đồng biến trong khoảng nào
Bước 4: Nồng độ thước máu đạt cực đại là bao nhiêu trong 6 phút sau khi tiêm là giá trị cực đại của hàm số \(C(x)\) trong khoảng \((0;6)\)
Lời giải chi tiết:
Hàm số trên xác định trên R
Ta có: \(y' = C'(x) = \frac{{30({x^2} + 2) - 30x.2x}}{{{{({x^2} + 2)}^2}}}\)
\( = \frac{{ - 30{x^2} + 60}}{{{{({x^2} + 2)}^2}}}\)
Xét \(y' = 0\) \( \Rightarrow - 30{x^2} + 60 = 0\) \( \Leftrightarrow x = \sqrt 2 \)
Ta có bảng biến thiên:
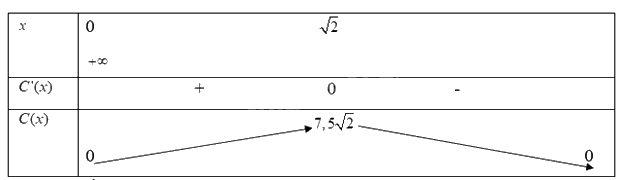
Từ bảng biến thiên, ta có :
a) Hàm số \(C(x)\)đồng biến trên khoảng \((0;7,5\sqrt 2 )\)hay nồng độ thước máu tăng từ sau khi tiêm đến \(7,5\sqrt 2 \)phút sau.
b) Hàm số \(C(x)\) đạt giá trị cực đại tại \(x = \sqrt 2 \)hay nồng độ thức máu đạt giá trị cực đại sau \(\sqrt 2 \) phút
Giải mục 2 trang 5,6,7 SGK Toán 12 tập 1 - Cùng khám phá: Hướng dẫn chi tiết và dễ hiểu
Mục 2 của SGK Toán 12 tập 1 thường xoay quanh các khái niệm và bài tập liên quan đến... (điền chủ đề chính của mục 2 vào đây). Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung chính của mục 2 trang 5,6,7 SGK Toán 12 tập 1
- Bài 1: (Mô tả ngắn gọn về bài 1 và mục đích của bài tập)
- Bài 2: (Mô tả ngắn gọn về bài 2 và mục đích của bài tập)
- Bài 3: (Mô tả ngắn gọn về bài 3 và mục đích của bài tập)
- ...
Giải chi tiết bài tập mục 2 trang 5,6,7 SGK Toán 12 tập 1
Bài 1: (Tiêu đề bài tập)
Đề bài: (Viết lại đề bài đầy đủ)
Lời giải:
- Bước 1: (Giải thích bước 1 và công thức sử dụng)
- Bước 2: (Giải thích bước 2 và công thức sử dụng)
- ...
- Kết luận: (Kết quả cuối cùng của bài tập)
Bài 2: (Tiêu đề bài tập)
Đề bài: (Viết lại đề bài đầy đủ)
Lời giải:
(Giải thích chi tiết bài tập tương tự như bài 1)
Bài 3: (Tiêu đề bài tập)
Đề bài: (Viết lại đề bài đầy đủ)
Lời giải:
(Giải thích chi tiết bài tập tương tự như bài 1)
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong mục 2 trang 5,6,7 SGK Toán 12 tập 1 một cách nhanh chóng và hiệu quả, các em cần:
- Nắm vững các định nghĩa và công thức liên quan.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị...
Lưu ý quan trọng
Trong quá trình giải bài tập, các em cần chú ý:
- Đọc kỹ đề bài để hiểu rõ yêu cầu.
- Kiểm tra lại kết quả trước khi nộp bài.
- Nếu gặp khó khăn, hãy hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ.
Tổng kết
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn khi giải các bài tập mục 2 trang 5,6,7 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao!
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác.