Giải mục 3 trang 60, 61, 62, 63, 64 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 60, 61, 62, 63, 64 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 60, 61, 62, 63, 64 sách giáo khoa Toán 12 tập 1. Bài viết này được tusach.vn biên soạn nhằm hỗ trợ các em trong quá trình học tập và ôn luyện môn Toán.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin giải quyết các bài tập tương tự.
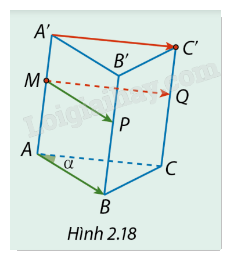
Cho hình lăng trụ ABC.A'B'C' có \(\widehat {BAC} = \alpha \). Gọi M là một điểm bất kỳ thuộc cạnh bên AA' (Hình 2.18). a) Vẽ hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) lần lượt bằng \(\overrightarrow {AB} \) và \(\overrightarrow {A'C'} \). ABC.MPQ có phải là hình lăng trụ không? Vì sao? b) Trong mặt phẳng (MPQ), hãy xác định góc giữa hai vectơ \(\overrightarrow {MP} \), \(\overrightarrow {MQ} \) và so sánh góc đó với \(\alpha \).
LT6
Trả lời câu hỏi Luyện tập 6 trang 61 SGK Toán 12 Cùng khám phá
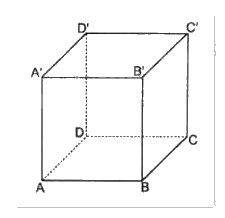
Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và
a) vecto \(\overrightarrow {AB} \);
b) vectơ \(\overrightarrow {AD} \);
c) vectơ \(\overrightarrow {{B^\prime }B} \).
Phương pháp giải:
Sử dụng các tính chất của hình lập phương để xác định góc của các vectơ.
Lời giải chi tiết:
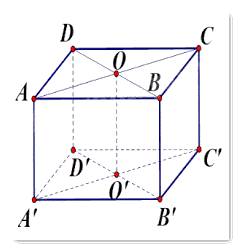
Gọi độ dài cạnh của hình lập phương là \(a\).
a) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AB} \):
Vì ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AB} \) là \(\widehat {BAC}\) và vì ABCD là hình vuông nên \(\widehat {BAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A'C'} ,\overrightarrow {AB} )} = 45^\circ \).
b) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AD} \):
Tương tự như câu a ta có: \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \) là \(\widehat {DAC}\) và vì ABCD là hình vuông nên \(\widehat {DAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A'C'}, \overrightarrow {AD} )} = 45^\circ \).
c) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {{B^\prime }B} \):
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
Vì O và O’ lần lượt là trung điểm của cạnh BD và B’D’ nên OO’ là đường trung bình của BB’D’D, suy ra \(\overrightarrow {B'B} = \overrightarrow {O'O} \).
Mà \(O'O \bot AC\) nên \(\widehat {(\overrightarrow {A'C'}, \overrightarrow {B'B} )} = 90^\circ \).
LT7
Trả lời câu hỏi Luyện tập 7 trang 63 SGK Toán 12 Cùng khám phá
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy tính:
a) \(\overrightarrow {AB'} .\overrightarrow {A'C'} ;\)
b) \(\overrightarrow {AB'} .\overrightarrow {BD} ;\)
c) \(\overrightarrow {A'C'} .\overrightarrow {BB'} .\)
Phương pháp giải:
- Xác định độ dài của các vectơ và góc giữa chúng dựa vào tính chất của hình lập phương.
- Sử dụng công thức tích vô hướng \(\vec u \cdot \vec v = |\vec u||\vec v|\cos \theta \) để tính.
Lời giải chi tiết:
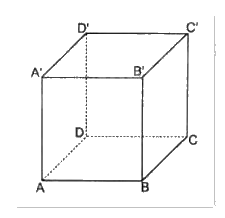
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
a) Tính \(\overrightarrow {AB'} \cdot \overrightarrow {A'C'} \).
Độ dài của \(|\overrightarrow {AB'} | = |\overrightarrow {A'C'} | = a\sqrt 2 \) (vì AB' và A'C' là các cạnh đường chéo của các mặt bên của hình lập phương).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Góc giữa \(\overrightarrow {AB'} \) và \(\overrightarrow {AC} \) là \({60^^\circ }\) vì chúng là hai cạnh của tam giác đều AB’C.
Do đó: \(\overrightarrow {AB'} .\overrightarrow {A'C'} = \left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {A'C'} } \right|.\cos 60^\circ = a\sqrt 2 .a\sqrt 2 .\frac{1}{2} = {a^2}\).
b) Tính \(\overrightarrow {AB'} \cdot \overrightarrow {BD} \).
Độ dài của \(|\overrightarrow {AB'} | = a\sqrt 2 \) và \(|\overrightarrow {BD} | = a\sqrt 2 \) (cả hai đều là đường chéo của các mặt bên của hình lập phương).
Từ B vẽ một vectơ \(\overrightarrow {BE} \) bằng với vectơ \(\overrightarrow {AB'} \).
Vì D đối xứng với E qua tâm của hình vuông BB’C’C nên đường trung tuyến của tam giác cân BED có độ dài là \(\frac{{a\sqrt 2 }}{2}\).
Suy ra: \(\widehat {DBE} = 2\arccos \left( {\frac{{a\sqrt 2 }}{2}:a\sqrt 2 } \right) = 2\arccos \left( {\frac{1}{2}} \right) = 2.60^\circ = 120^\circ \).
Góc giữa \(\overrightarrow {AB'} \) và \(\overrightarrow {BD} \) cũng là góc giữa \(\overrightarrow {BE} \)và \(\overrightarrow {BD} \) là \(\widehat {DBE}\).
Do đó: \(\overrightarrow {AB'} .\overrightarrow {BD} = \left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BD} } \right|.\cos 120^\circ = a\sqrt 2 .a\sqrt 2 .\left( { - \frac{1}{2}} \right) = - {a^2}\).
c) Tính \(\overrightarrow {A'C'} \cdot \overrightarrow {BB'} \).
Độ dài của \(|\overrightarrow {A'C'} | = a\sqrt 2 \) và \(|\overrightarrow {BB'} | = a\).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} ,\overrightarrow {BB'} = \overrightarrow {AA'} \).
Do \(\overrightarrow {AC} \) và \(\overrightarrow {AA'} \) vuông góc với nhau nên góc giữa \(\overrightarrow {A'C'} \) và \(\overrightarrow {BB'} \) Là 90°.
Suy ra: \(\overrightarrow {A'C'} .\overrightarrow {BB'} = \left| {\overrightarrow {A'C'} } \right|.\left| {\overrightarrow {BB'} } \right|.\cos 90^\circ = a\sqrt 2 .a.0 = 0\).
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 62 SGK Toán 12 Cùng khám phá
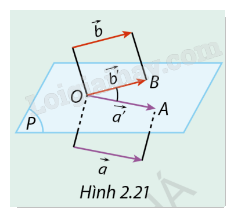
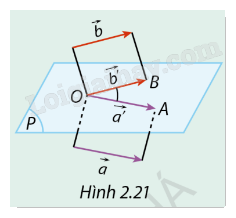
Trong không gian, cho hai vectơ \(\vec a,\vec b\) khác \(\vec 0\). Từ một điểm \(O\) tuỳ ý trong không gian, vẽ các vectơ \(\overrightarrow {{a^\prime }} ,\overrightarrow {{b^\prime }} \) sao cho \(\overrightarrow {{a^\prime }} = \vec a\), \(\overrightarrow {{b^\prime }} = \vec b\). (P) là mặt phẳng chứa giá của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) (Hình 2.21).
a) Trong mặt phẳng \((P)\), hãy viết biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \).
b) Hãy so sánh \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) với \(|\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\).
Phương pháp giải:
1. Sử dụng định nghĩa của tích vô hướng trong mặt phẳng \((P)\).
2. Sử dụng công thức của tích vô hướng để so sánh các biểu thức.
Lời giải chi tiết:
a) Trong mặt phẳng \((P)\), biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) được tính như sau:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\overrightarrow {{a^\prime }} | \cdot |\overrightarrow {{b^\prime }} | \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
b) Vì \(\overrightarrow {{a^\prime }} = \vec a\) và \(\overrightarrow {{b^\prime }} = \vec b\), nên:
\(|\overrightarrow {{a^\prime }} | = |\vec a|,|\overrightarrow {{b^\prime }} | = |\vec b|\)
Do đó, ta có:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
Biểu thức này cho thấy rằng tích vô hướng của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) là bằng tích của độ lớn của hai vectơ \(\vec a\) và \(\vec b\) với cosin của góc giữa chúng. Vì vậy:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\)
Điều này chứng minh rằng tích vô hướng của \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) bằng tích vô hướng của \(\vec a\) và \(\vec b\).
LT5
Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cùng khám phá
Cho hình lăng trụ ABC.A'B'C' có \(\widehat {BAC} = \alpha \). Gọi M là một điểm bất kỳ thuộc cạnh bên AA' (Hình 2.18).
a) Vẽ hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) lần lượt bằng \(\overrightarrow {AB} \) và \(\overrightarrow {A'C'} \). ABC.MPQ có phải là hình lăng trụ không? Vì sao?
b) Trong mặt phẳng (MPQ), hãy xác định góc giữa hai vectơ \(\overrightarrow {MP} \), \(\overrightarrow {MQ} \) và so sánh góc đó với \(\alpha \).
Phương pháp giải:
- Sử dụng định nghĩa và tính chất của vectơ kết hợp với khái niệm và các tính chất của hình lăng trụ.
- Hình lăng trụ là hình đa diện bao gồm 2 đáy nằm trên hai mặt phẳng song song và là hai đa giác bằng nhau.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {MP} = \overrightarrow {AB} \) suy ra MP = AB và MP // AB (1)
Tương tự: \(\overrightarrow {MQ} = \overrightarrow {A'C'} \) suy ra MQ = A’C’ = AC và MQ // A’C’ // AC (2)
Từ (1) và (2) suy ra \(\Delta MPQ = \Delta ABC\).
ABC.MPQ có hai đáy song song và bằng nhau nên ABC.MPQ là hình lăng trụ.
b) Vì \(\Delta MPQ = \Delta ABC\) nên \(\widehat {PMQ} = \widehat {BAC} = \alpha \).
Mà góc giữa hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) là góc\(\widehat {PMQ}\).
Vậy \(\widehat {(\overrightarrow {MP} ,\overrightarrow {MQ} )} = \alpha \).
LT9
Trả lời câu hỏi Luyện tập 9 trang 64 SGK Toán 12 Cùng khám phá
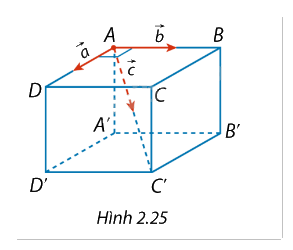
Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương ABCD.A'B'C'D'. Chất điểm chịu tác động bởi ba lực \(\vec a\), \(\vec b\), \(\vec c\) lần lượt cùng hướng với \(\overrightarrow {AD} \), \(\overrightarrow {AB} \) và \(\overrightarrow {AC'} \) như Hình 2.25. Cường độ của các lực \(\vec a\), \(\vec b\) và \(\vec c\) tương ứng là \(10{\rm{ N}}\), \(10{\rm{ N}}\) và \(20{\rm{ N}}\). Tính cường độ hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) (làm tròn kết quả đến hàng phần mười).
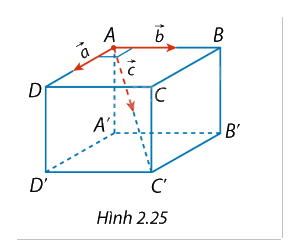
Phương pháp giải:
- Sử dụng công thức quy tắc hình bình hành để tính tổng hợp lực của \(\vec a\), \(\vec b\).
\(F{}^\text{2}=\text{}{{F}_{1}}{}^\text{2}+{{F}_{2}}{}^\text{2}+2.{{}_{1}}.{{F}_{2}}.\cos \alpha \).
- Sau đó sử dụng kết quả vừa tính để tính tổng hợp lực với \(\vec c\).
Lời giải chi tiết:
Vì ABCD.A’B’C’D’ là hình lập phương nên góc giữa \(\overrightarrow {AD} \)và \(\overrightarrow {AB} \) là 90°.
Suy ra lực \(\vec a\) vuông góc với \(\vec b\). Vậy hợp lực của hai lực \(\vec a\) và \(\vec b\) là:
\(\overrightarrow {{F_{ab}}} = \overrightarrow {{F_a}} + \overrightarrow {{F_b}} \Rightarrow {F_{ab}} = \sqrt {{F_a}^2 + {F_b}^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 N\).
Vì tam giác ACC’ là tam giác vuông tại C nên ta có:
\(AC' = \sqrt {A{C^2} + CC{'^2}} = \sqrt {A{C^2} + \frac{{A{C^2}}}{2}} = AC\sqrt {\frac{3}{2}} \) (vì CC’ là cạnh bên của hình lập phương còn AC là đường chéo của mặt bên nên \(CC' = \frac{{AC}}{{\sqrt 2 }}\)).
\(\cos \widehat {CAC'} = \frac{{AC}}{{AC'}} = \frac{{AC}}{{AC\sqrt {\frac{3}{2}} }} = \frac{{\sqrt 6 }}{3}\).
Hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) là:
\(F = \sqrt {{F_{ab}}^2 + F_c^2 + 2.{F_{ab}}.{F_c}.\cos \widehat {CAC'}} = \sqrt {{{\left( {10\sqrt 2 } \right)}^2} + {{20}^2} + 2.10\sqrt 2 .20.\frac{{\sqrt 6 }}{3}} = 32,6N\).
LT8
Trả lời câu hỏi Luyện tập 8 trang 63 SGK Toán 12 Cùng khám phá
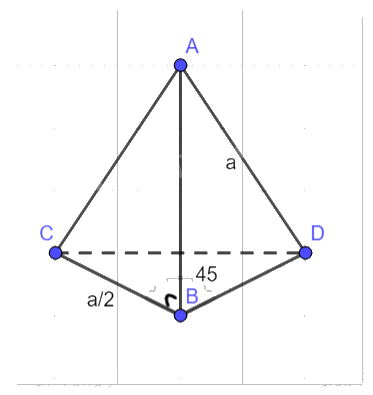
Cho tứ diện ABCD có \(DA = DB = a\), \(BC = \frac{a}{2}\), \(AB \bot BC\) và \(\widehat {CBD} = {45^^\circ }\). Tính góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
Phương pháp giải:
- Tính tích vô hướng của \(\overrightarrow {BC} .\overrightarrow {BD} \), từ đó suy ra mối liên hệ với tích vô hướng của hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
- Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}}\).
Lời giải chi tiết:
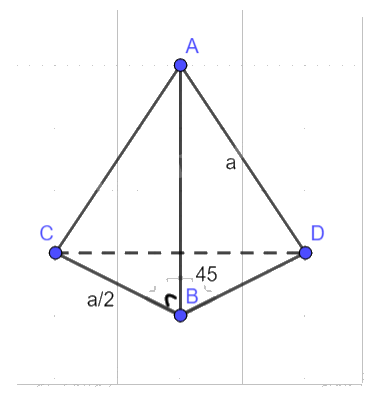
Ta có: \(\overrightarrow {BC} .\overrightarrow {BD} = BC.DB.\cos 45^\circ = \frac{a}{2}.a.\frac{{\sqrt 2 }}{2} = \frac{{{a^2}\sqrt 2 }}{4}\).
Mà: \(\overrightarrow {BC} .\overrightarrow {AD} = \overrightarrow {BC} .\overrightarrow {BD} + \overrightarrow {BC} .\overrightarrow {AB} \).
Suy ra: \(\overrightarrow {BC} .\overrightarrow {AD} = \frac{{{a^2}\sqrt 2 }}{4} + 0 = \frac{{{a^2}\sqrt 2 }}{4}\)(vì \(AB \bot BC\) nên \(\overrightarrow {BC} .\overrightarrow {AB} = 0\)).
Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}} = \frac{{\frac{{{a^2}\sqrt 2 }}{4}}}{{a.\frac{a}{2}}} = \frac{{\sqrt 2 }}{2}\).
Vậy góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) là \(\arccos \left( {\frac{{\sqrt 2 }}{2}} \right) = 45^\circ \).
- LT5
- LT6
- HĐ6
- LT7
- LT8
- LT9
Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cùng khám phá
Cho hình lăng trụ ABC.A'B'C' có \(\widehat {BAC} = \alpha \). Gọi M là một điểm bất kỳ thuộc cạnh bên AA' (Hình 2.18).
a) Vẽ hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) lần lượt bằng \(\overrightarrow {AB} \) và \(\overrightarrow {A'C'} \). ABC.MPQ có phải là hình lăng trụ không? Vì sao?
b) Trong mặt phẳng (MPQ), hãy xác định góc giữa hai vectơ \(\overrightarrow {MP} \), \(\overrightarrow {MQ} \) và so sánh góc đó với \(\alpha \).
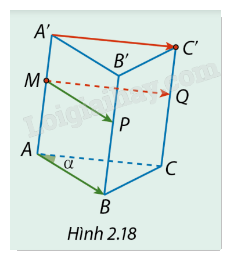
Phương pháp giải:
- Sử dụng định nghĩa và tính chất của vectơ kết hợp với khái niệm và các tính chất của hình lăng trụ.
- Hình lăng trụ là hình đa diện bao gồm 2 đáy nằm trên hai mặt phẳng song song và là hai đa giác bằng nhau.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {MP} = \overrightarrow {AB} \) suy ra MP = AB và MP // AB (1)
Tương tự: \(\overrightarrow {MQ} = \overrightarrow {A'C'} \) suy ra MQ = A’C’ = AC và MQ // A’C’ // AC (2)
Từ (1) và (2) suy ra \(\Delta MPQ = \Delta ABC\).
ABC.MPQ có hai đáy song song và bằng nhau nên ABC.MPQ là hình lăng trụ.
b) Vì \(\Delta MPQ = \Delta ABC\) nên \(\widehat {PMQ} = \widehat {BAC} = \alpha \).
Mà góc giữa hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) là góc\(\widehat {PMQ}\).
Vậy \(\widehat {(\overrightarrow {MP} ,\overrightarrow {MQ} )} = \alpha \).
Trả lời câu hỏi Luyện tập 6 trang 61 SGK Toán 12 Cùng khám phá
Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và
a) vecto \(\overrightarrow {AB} \);
b) vectơ \(\overrightarrow {AD} \);
c) vectơ \(\overrightarrow {{B^\prime }B} \).
Phương pháp giải:
Sử dụng các tính chất của hình lập phương để xác định góc của các vectơ.
Lời giải chi tiết:
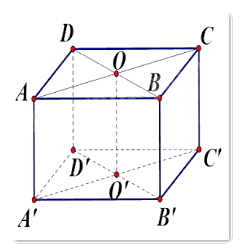
Gọi độ dài cạnh của hình lập phương là \(a\).
a) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AB} \):
Vì ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AB} \) là \(\widehat {BAC}\) và vì ABCD là hình vuông nên \(\widehat {BAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A'C'} ,\overrightarrow {AB} )} = 45^\circ \).
b) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AD} \):
Tương tự như câu a ta có: \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \) là \(\widehat {DAC}\) và vì ABCD là hình vuông nên \(\widehat {DAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A'C'}, \overrightarrow {AD} )} = 45^\circ \).
c) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {{B^\prime }B} \):
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
Vì O và O’ lần lượt là trung điểm của cạnh BD và B’D’ nên OO’ là đường trung bình của BB’D’D, suy ra \(\overrightarrow {B'B} = \overrightarrow {O'O} \).
Mà \(O'O \bot AC\) nên \(\widehat {(\overrightarrow {A'C'}, \overrightarrow {B'B} )} = 90^\circ \).
Trả lời câu hỏi Hoạt động 6 trang 62 SGK Toán 12 Cùng khám phá
Trong không gian, cho hai vectơ \(\vec a,\vec b\) khác \(\vec 0\). Từ một điểm \(O\) tuỳ ý trong không gian, vẽ các vectơ \(\overrightarrow {{a^\prime }} ,\overrightarrow {{b^\prime }} \) sao cho \(\overrightarrow {{a^\prime }} = \vec a\), \(\overrightarrow {{b^\prime }} = \vec b\). (P) là mặt phẳng chứa giá của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) (Hình 2.21).
a) Trong mặt phẳng \((P)\), hãy viết biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \).
b) Hãy so sánh \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) với \(|\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\).
Phương pháp giải:
1. Sử dụng định nghĩa của tích vô hướng trong mặt phẳng \((P)\).
2. Sử dụng công thức của tích vô hướng để so sánh các biểu thức.
Lời giải chi tiết:
a) Trong mặt phẳng \((P)\), biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) được tính như sau:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\overrightarrow {{a^\prime }} | \cdot |\overrightarrow {{b^\prime }} | \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
b) Vì \(\overrightarrow {{a^\prime }} = \vec a\) và \(\overrightarrow {{b^\prime }} = \vec b\), nên:
\(|\overrightarrow {{a^\prime }} | = |\vec a|,|\overrightarrow {{b^\prime }} | = |\vec b|\)
Do đó, ta có:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
Biểu thức này cho thấy rằng tích vô hướng của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) là bằng tích của độ lớn của hai vectơ \(\vec a\) và \(\vec b\) với cosin của góc giữa chúng. Vì vậy:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\)
Điều này chứng minh rằng tích vô hướng của \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) bằng tích vô hướng của \(\vec a\) và \(\vec b\).
Trả lời câu hỏi Luyện tập 7 trang 63 SGK Toán 12 Cùng khám phá
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy tính:
a) \(\overrightarrow {AB'} .\overrightarrow {A'C'} ;\)
b) \(\overrightarrow {AB'} .\overrightarrow {BD} ;\)
c) \(\overrightarrow {A'C'} .\overrightarrow {BB'} .\)
Phương pháp giải:
- Xác định độ dài của các vectơ và góc giữa chúng dựa vào tính chất của hình lập phương.
- Sử dụng công thức tích vô hướng \(\vec u \cdot \vec v = |\vec u||\vec v|\cos \theta \) để tính.
Lời giải chi tiết:
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
a) Tính \(\overrightarrow {AB'} \cdot \overrightarrow {A'C'} \).
Độ dài của \(|\overrightarrow {AB'} | = |\overrightarrow {A'C'} | = a\sqrt 2 \) (vì AB' và A'C' là các cạnh đường chéo của các mặt bên của hình lập phương).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Góc giữa \(\overrightarrow {AB'} \) và \(\overrightarrow {AC} \) là \({60^^\circ }\) vì chúng là hai cạnh của tam giác đều AB’C.
Do đó: \(\overrightarrow {AB'} .\overrightarrow {A'C'} = \left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {A'C'} } \right|.\cos 60^\circ = a\sqrt 2 .a\sqrt 2 .\frac{1}{2} = {a^2}\).
b) Tính \(\overrightarrow {AB'} \cdot \overrightarrow {BD} \).
Độ dài của \(|\overrightarrow {AB'} | = a\sqrt 2 \) và \(|\overrightarrow {BD} | = a\sqrt 2 \) (cả hai đều là đường chéo của các mặt bên của hình lập phương).
Từ B vẽ một vectơ \(\overrightarrow {BE} \) bằng với vectơ \(\overrightarrow {AB'} \).
Vì D đối xứng với E qua tâm của hình vuông BB’C’C nên đường trung tuyến của tam giác cân BED có độ dài là \(\frac{{a\sqrt 2 }}{2}\).
Suy ra: \(\widehat {DBE} = 2\arccos \left( {\frac{{a\sqrt 2 }}{2}:a\sqrt 2 } \right) = 2\arccos \left( {\frac{1}{2}} \right) = 2.60^\circ = 120^\circ \).
Góc giữa \(\overrightarrow {AB'} \) và \(\overrightarrow {BD} \) cũng là góc giữa \(\overrightarrow {BE} \)và \(\overrightarrow {BD} \) là \(\widehat {DBE}\).
Do đó: \(\overrightarrow {AB'} .\overrightarrow {BD} = \left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BD} } \right|.\cos 120^\circ = a\sqrt 2 .a\sqrt 2 .\left( { - \frac{1}{2}} \right) = - {a^2}\).
c) Tính \(\overrightarrow {A'C'} \cdot \overrightarrow {BB'} \).
Độ dài của \(|\overrightarrow {A'C'} | = a\sqrt 2 \) và \(|\overrightarrow {BB'} | = a\).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} ,\overrightarrow {BB'} = \overrightarrow {AA'} \).
Do \(\overrightarrow {AC} \) và \(\overrightarrow {AA'} \) vuông góc với nhau nên góc giữa \(\overrightarrow {A'C'} \) và \(\overrightarrow {BB'} \) Là 90°.
Suy ra: \(\overrightarrow {A'C'} .\overrightarrow {BB'} = \left| {\overrightarrow {A'C'} } \right|.\left| {\overrightarrow {BB'} } \right|.\cos 90^\circ = a\sqrt 2 .a.0 = 0\).
Trả lời câu hỏi Luyện tập 8 trang 63 SGK Toán 12 Cùng khám phá
Cho tứ diện ABCD có \(DA = DB = a\), \(BC = \frac{a}{2}\), \(AB \bot BC\) và \(\widehat {CBD} = {45^^\circ }\). Tính góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
Phương pháp giải:
- Tính tích vô hướng của \(\overrightarrow {BC} .\overrightarrow {BD} \), từ đó suy ra mối liên hệ với tích vô hướng của hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
- Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}}\).
Lời giải chi tiết:
Ta có: \(\overrightarrow {BC} .\overrightarrow {BD} = BC.DB.\cos 45^\circ = \frac{a}{2}.a.\frac{{\sqrt 2 }}{2} = \frac{{{a^2}\sqrt 2 }}{4}\).
Mà: \(\overrightarrow {BC} .\overrightarrow {AD} = \overrightarrow {BC} .\overrightarrow {BD} + \overrightarrow {BC} .\overrightarrow {AB} \).
Suy ra: \(\overrightarrow {BC} .\overrightarrow {AD} = \frac{{{a^2}\sqrt 2 }}{4} + 0 = \frac{{{a^2}\sqrt 2 }}{4}\)(vì \(AB \bot BC\) nên \(\overrightarrow {BC} .\overrightarrow {AB} = 0\)).
Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}} = \frac{{\frac{{{a^2}\sqrt 2 }}{4}}}{{a.\frac{a}{2}}} = \frac{{\sqrt 2 }}{2}\).
Vậy góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) là \(\arccos \left( {\frac{{\sqrt 2 }}{2}} \right) = 45^\circ \).
Trả lời câu hỏi Luyện tập 9 trang 64 SGK Toán 12 Cùng khám phá
Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương ABCD.A'B'C'D'. Chất điểm chịu tác động bởi ba lực \(\vec a\), \(\vec b\), \(\vec c\) lần lượt cùng hướng với \(\overrightarrow {AD} \), \(\overrightarrow {AB} \) và \(\overrightarrow {AC'} \) như Hình 2.25. Cường độ của các lực \(\vec a\), \(\vec b\) và \(\vec c\) tương ứng là \(10{\rm{ N}}\), \(10{\rm{ N}}\) và \(20{\rm{ N}}\). Tính cường độ hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) (làm tròn kết quả đến hàng phần mười).
Phương pháp giải:
- Sử dụng công thức quy tắc hình bình hành để tính tổng hợp lực của \(\vec a\), \(\vec b\).
\(F{}^\text{2}=\text{}{{F}_{1}}{}^\text{2}+{{F}_{2}}{}^\text{2}+2.{{}_{1}}.{{F}_{2}}.\cos \alpha \).
- Sau đó sử dụng kết quả vừa tính để tính tổng hợp lực với \(\vec c\).
Lời giải chi tiết:
Vì ABCD.A’B’C’D’ là hình lập phương nên góc giữa \(\overrightarrow {AD} \)và \(\overrightarrow {AB} \) là 90°.
Suy ra lực \(\vec a\) vuông góc với \(\vec b\). Vậy hợp lực của hai lực \(\vec a\) và \(\vec b\) là:
\(\overrightarrow {{F_{ab}}} = \overrightarrow {{F_a}} + \overrightarrow {{F_b}} \Rightarrow {F_{ab}} = \sqrt {{F_a}^2 + {F_b}^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 N\).
Vì tam giác ACC’ là tam giác vuông tại C nên ta có:
\(AC' = \sqrt {A{C^2} + CC{'^2}} = \sqrt {A{C^2} + \frac{{A{C^2}}}{2}} = AC\sqrt {\frac{3}{2}} \) (vì CC’ là cạnh bên của hình lập phương còn AC là đường chéo của mặt bên nên \(CC' = \frac{{AC}}{{\sqrt 2 }}\)).
\(\cos \widehat {CAC'} = \frac{{AC}}{{AC'}} = \frac{{AC}}{{AC\sqrt {\frac{3}{2}} }} = \frac{{\sqrt 6 }}{3}\).
Hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) là:
\(F = \sqrt {{F_{ab}}^2 + F_c^2 + 2.{F_{ab}}.{F_c}.\cos \widehat {CAC'}} = \sqrt {{{\left( {10\sqrt 2 } \right)}^2} + {{20}^2} + 2.10\sqrt 2 .20.\frac{{\sqrt 6 }}{3}} = 32,6N\).
Giải mục 3 trang 60, 61, 62, 63, 64 SGK Toán 12 tập 1 - Cùng khám phá
Mục 3 trong SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các dạng bài tập về tính đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, và giải các bài toán liên quan đến đạo hàm. Việc nắm vững kiến thức về đạo hàm là vô cùng quan trọng, vì nó là nền tảng cho nhiều chương trình học tiếp theo và cũng xuất hiện thường xuyên trong các kỳ thi quan trọng như THPT Quốc gia.
Nội dung chính của Mục 3 SGK Toán 12 tập 1
- Đạo hàm của hàm số: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm. Các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Đạo hàm của các hàm số thường gặp: Đạo hàm của hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác và hàm số lượng giác ngược.
- Ứng dụng đạo hàm để khảo sát hàm số: Tìm cực trị, điểm uốn, khoảng đơn điệu và giới hạn của hàm số.
- Bài tập vận dụng: Giải các bài tập về tính đạo hàm, khảo sát hàm số và ứng dụng đạo hàm để giải các bài toán thực tế.
Giải chi tiết các bài tập trang 60, 61, 62, 63, 64
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3, trang 60, 61, 62, 63, 64 SGK Toán 12 tập 1:
Bài 1 (Trang 60)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1.
Lời giải:
f'(x) = 3x2 - 4x + 5
Bài 2 (Trang 61)
Đề bài: Tính đạo hàm của hàm số g(x) = sin(2x) + cos(x).
Lời giải:
g'(x) = 2cos(2x) - sin(x)
Bài 3 (Trang 62)
Đề bài: Tìm cực trị của hàm số h(x) = x3 - 3x2 + 2.
Lời giải:
h'(x) = 3x2 - 6x = 3x(x - 2)
Giải phương trình h'(x) = 0, ta được x = 0 và x = 2.
Khảo sát dấu của h'(x) trên các khoảng (-∞, 0), (0, 2), (2, +∞) để xác định cực đại và cực tiểu.
Mẹo học tốt môn Toán 12
- Nắm vững kiến thức cơ bản: Đảm bảo bạn hiểu rõ các định nghĩa, định lý và công thức trong chương trình học.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
- Sử dụng tài liệu tham khảo: Tham khảo các sách giáo khoa, sách bài tập, đề thi và các nguồn tài liệu trực tuyến khác để bổ sung kiến thức và mở rộng hiểu biết.
- Học nhóm: Trao đổi kiến thức và kinh nghiệm với bạn bè để cùng nhau tiến bộ.
- Tìm kiếm sự giúp đỡ: Đừng ngần ngại hỏi thầy cô giáo hoặc các bạn học giỏi khi gặp khó khăn.
tusach.vn hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên, các em sẽ học tốt môn Toán 12 và đạt được kết quả cao trong các kỳ thi sắp tới. Chúc các em thành công!